2.1 Frequency

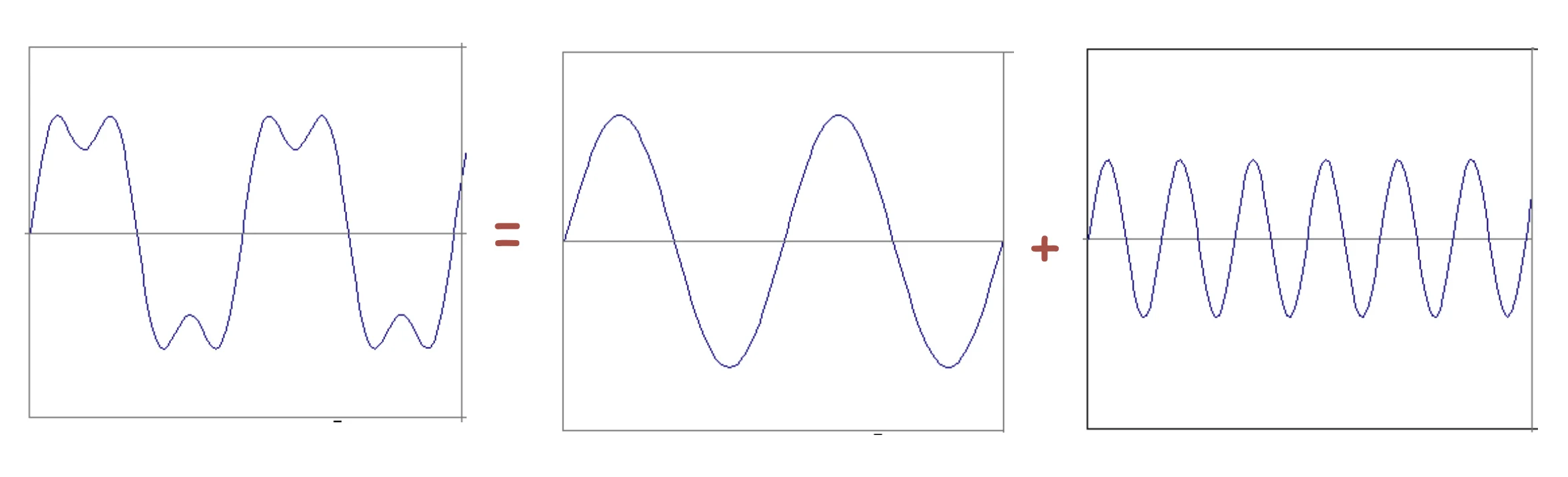
A sum of sines

Building blocks:

Asin(ωx+ϕ)Asin(\omega x + \phi)

Frequency Spectra

Example

g(t)=sin(2πft)+13sin(2π(3f)t)g(t) = sin(2\pi f t) + \frac{1}{3}sin(2\pi(3f)t)

clipboard.png

How to construct a square wave

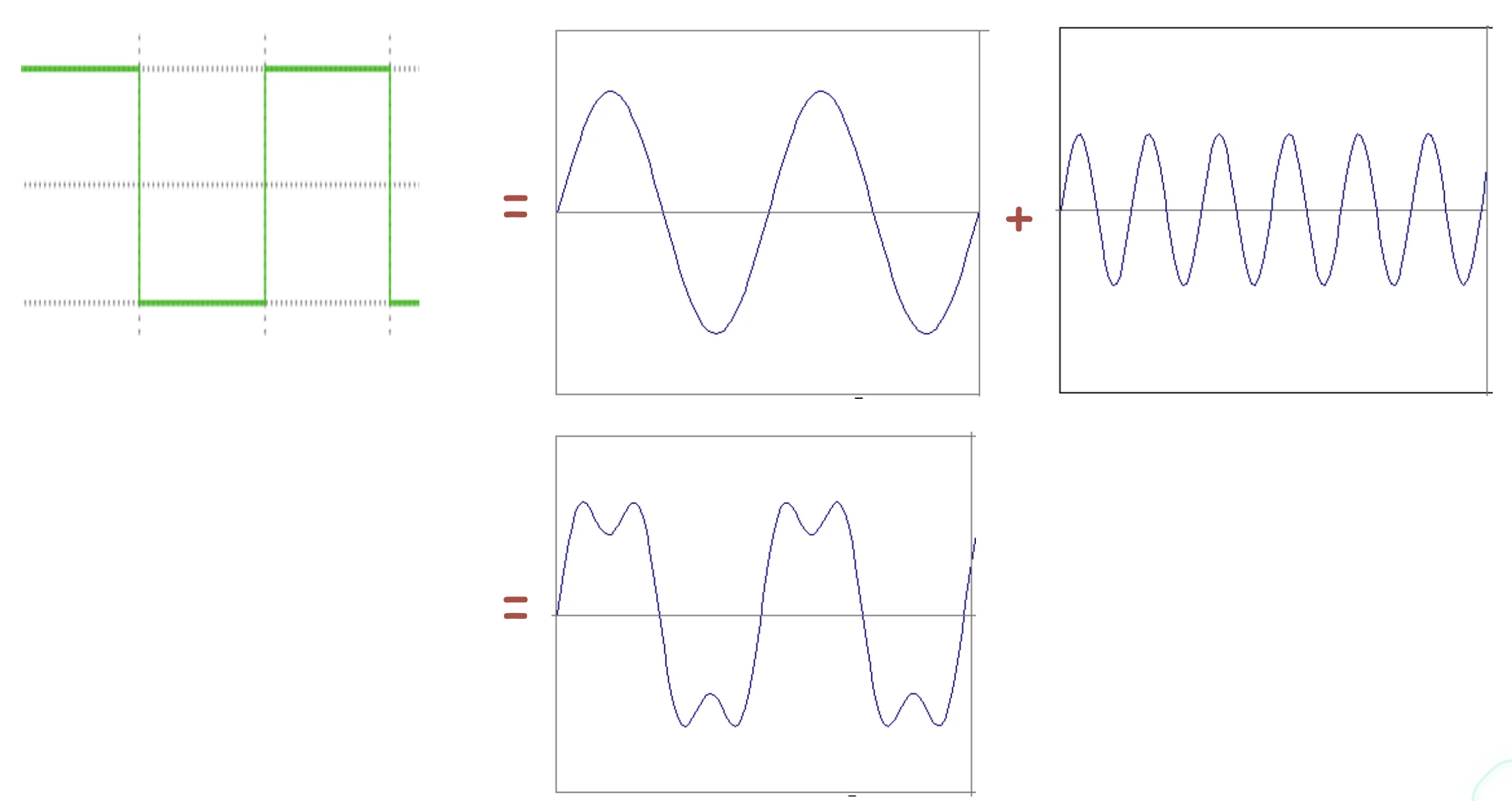
clipboard.png

  • Add enough of these signals at decreasing amplitudes as you increase the frequency of this sinusoid. Then, the sum of signals converges to a square wave
A∑k=1∞1ksin(2πkt)A\sum_{k = 1}^{\infty} \frac{1}{k} sin(2 \pi k t)

Fourier Analysis in Images

clipboard.png

Fourier Transform

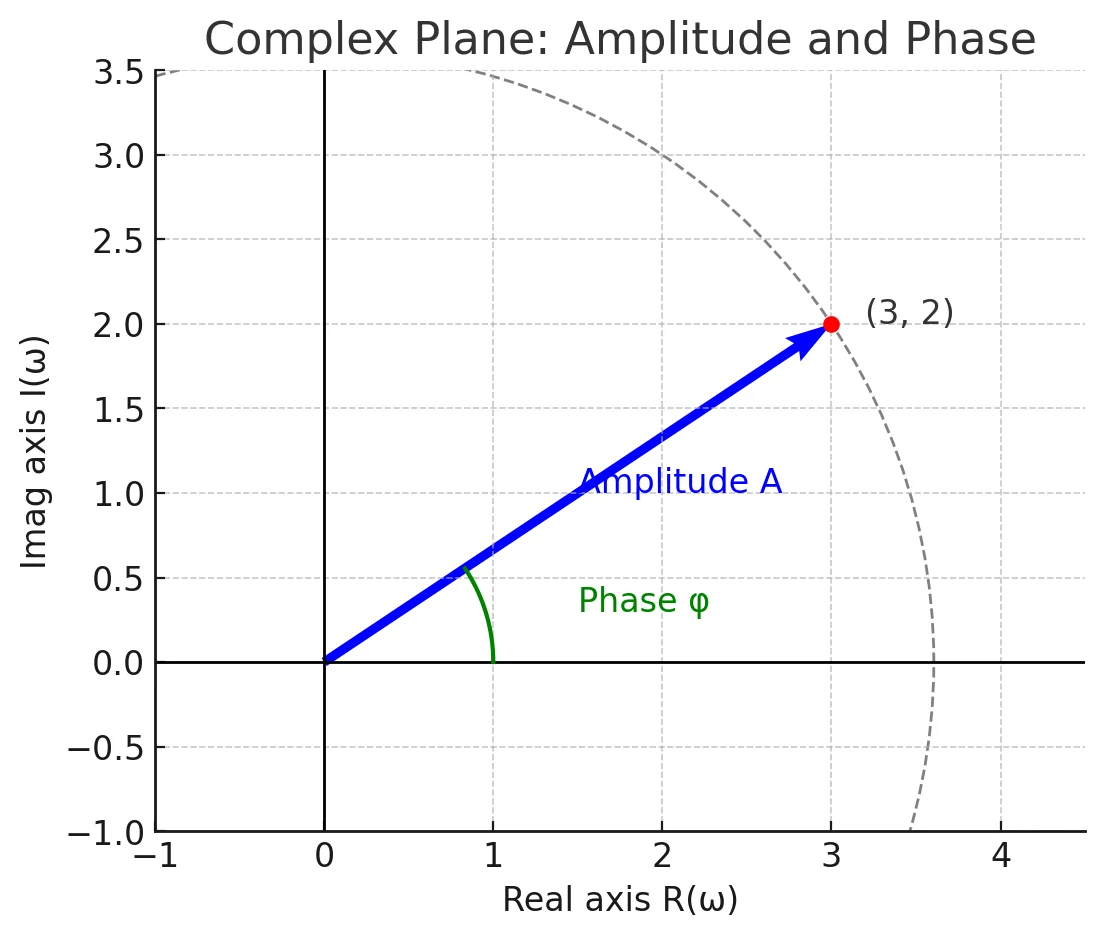
  • Fourier transform stores the amplitude and phase at each frequency

  • Amplitude: encodes the number of signals at a particular frequency

  • Phase: encodes spatial information

clipboard.png

1. Amplitude Formula

A=±R(ω)2+I(ω)2A = \pm \sqrt{R(\omega)^2 + I(\omega)^2}

where:

  • R(ω)R(\omega): the real part of a complex function (often a Fourier transform).

  • I(ω)I(\omega): the imaginary part.

  • R(ω)+iI(ω)R(\omega) + iI(\omega): a complex number representing a signal at frequency ω\omega.

∙\bullet Amplitude on Cosine Wave

# Time vector
t = np.linspace(0, 2*np.pi, 500)

# Parameters
omega = 1.0 # frequency
phi = np.pi/4 # fixed phase

# Different amplitudes
A1 = 0.5
A2 = 1.0
A3 = 1.5

# Signals
y1 = A1 * np.cos(omega*t + phi)
y2 = A2 * np.cos(omega*t + phi)
y3 = A3 * np.cos(omega*t + phi)

# Plot
plt.figure(figsize=(8,5))
plt.plot(t, y1, label=r'$A = 0.5$', linewidth=2)
plt.plot(t, y2, label=r'$A = 1.0$', linewidth=2)
plt.plot(t, y3, label=r'$A = 1.5$', linewidth=2)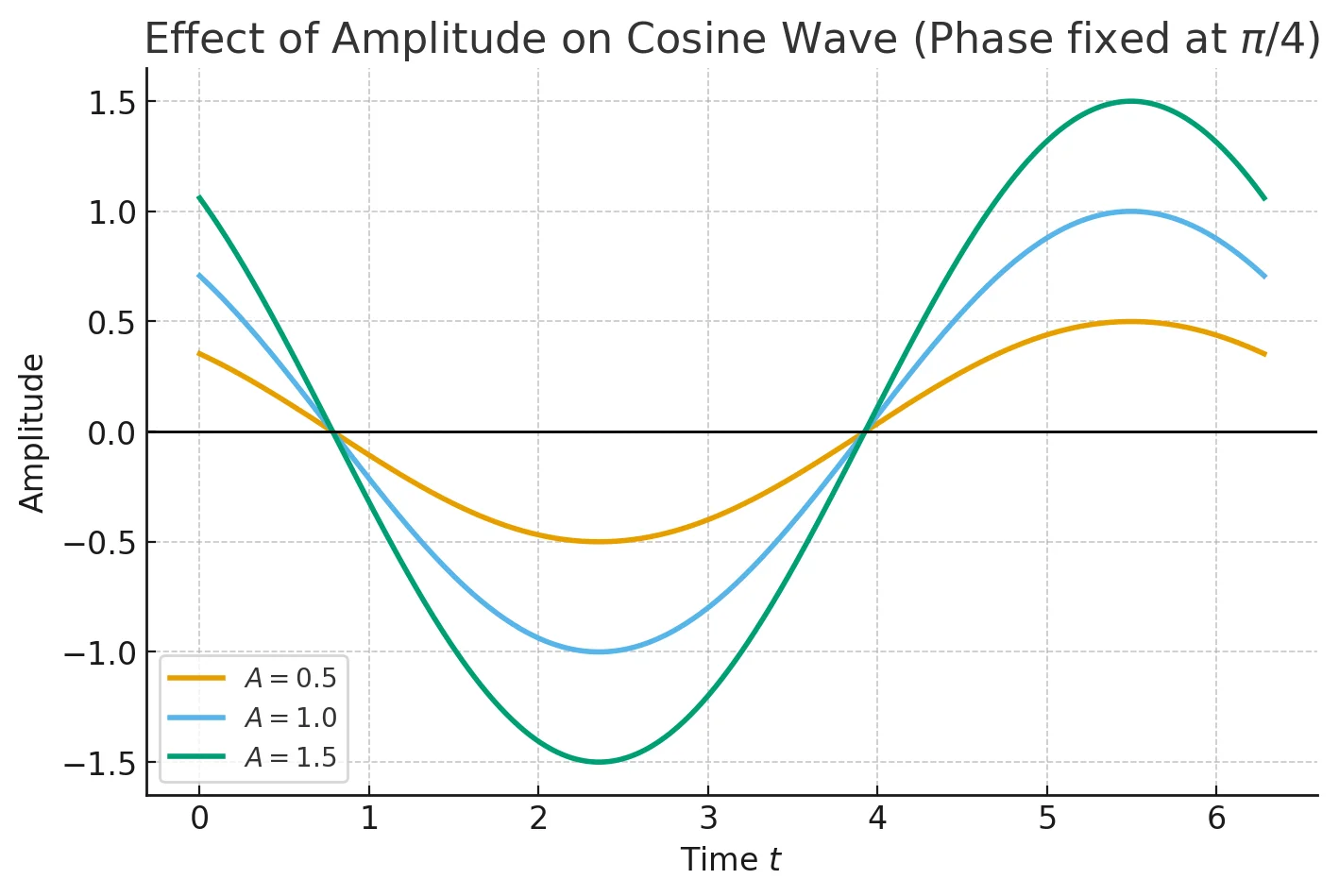

clipboard.png

Note

The amplitude (or magnitude) is just the length of this complex number in the complex plane. Pythagorean theorem:

∣R+iI∣=R2+I2|R + iI| = \sqrt{R^2 + I^2}

2. Phase Formula

ϕ=tan⁡−1 ⁣(I(ω)R(ω))\phi = \tan^{-1}\!\left(\frac{I(\omega)}{R(\omega)}\right)

  • The phase angle describes how much the sinusoidal signal is shifted horizontally relative to a cosine (or sine).

  • In the complex plane, the phase is the angle made by (R(ω),I(ω))(R(\omega), I(\omega)) vector with the positive real axis.

∙\bullet Shift on Cosine Wave

# Time vector
t = np.linspace(0, 2*np.pi, 500)

# Parameters
A = 1.0 # amplitude
omega = 1.0 # frequency

# Different phases
phi1 = 0
phi2 = np.pi/4 # 45 degrees
phi3 = np.pi/2 # 90 degrees

# Signals
y1 = A * np.cos(omega*t + phi1)
y2 = A * np.cos(omega*t + phi2)
y3 = A * np.cos(omega*t + phi3)

# Plot
plt.figure(figsize=(8,5))
plt.plot(t, y1, label=r'$\phi = 0$', linewidth=2)
plt.plot(t, y2, label=r'$\phi = \pi/4$', linewidth=2)
plt.plot(t, y3, label=r'$\phi = \pi/2$', linewidth=2)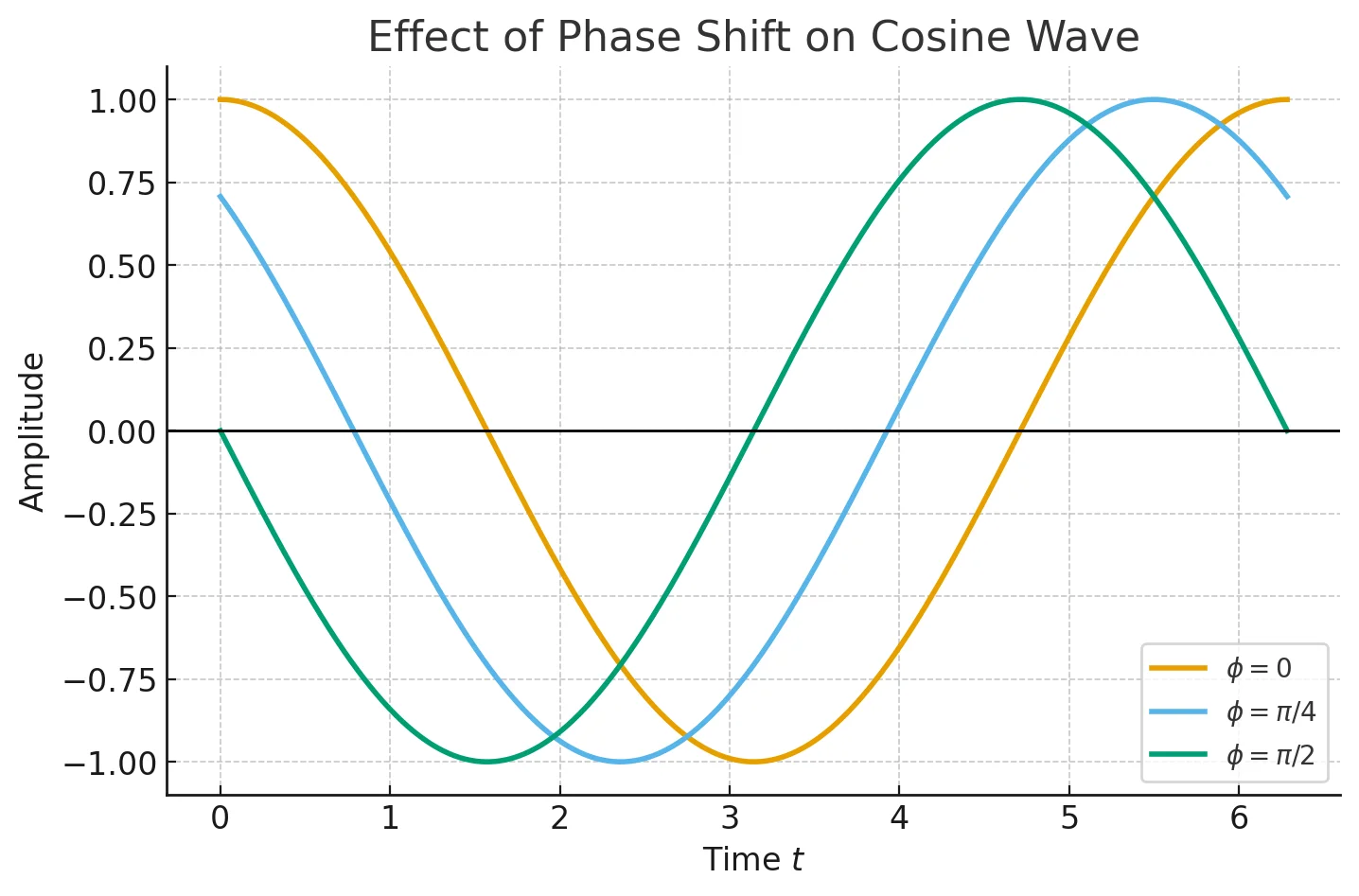

clipboard.png

Note

In practice, we often use atan2(I, R) instead of, because atan2 takes into account which quadrant the point lies in (avoiding sign ambiguities).

3. Euler’s Formula

eiθ=cos(θ)+isin(θ)e^{i\theta} = cos(\theta) + isin(\theta)

  • Exponentials with imaginary exponents represent rotations in the complex plane.

  • The real part gives a cosine, and the imaginary part gives a sine.

So when we write:

Aeiϕ=R(ω)+iI(ω)Ae^{i\phi} = R(\omega) + iI(\omega)

  • AA: the amplitude (the radius in the complex plane),

  • ϕ\phi: the phase (the angle).

Tip

The derivation is shown in Euler’s Formula

Integration and Fourier Transform

Important

Imaginary number ii is presented with jj due to mathematical convention

∙\bullet General Form

H(ω)=F{h(x)}=AejϕH(\omega) = \mathcal{F}\{h(x)\} = Ae^{j\phi}
  • F\mathcal{F}: Fourier Transform
  • H(ω)H(\omega): frequency domain

∙\bullet Continuous Fourier Transform (CFT)

used when h(x)h(x) is a continuous signal

H(ω)=∫−∞∞h(x)e−jωxdxH(\omega) = \int_{-\infty}^{\infty} h(x)e^{-j\omega x} dx
  • projects the singal onto complex exponentials e−jωxe^{-j\omega x}
  • At each frequency ω\omega, it computes the amount of that frequency is present in the singal

∙\bullet Discrete Fourier Transform (DFT)

used when h(x)h(x) is a discrete signal

H(k)=1N∑x=0N−1h(x)e−j2πNkxH(k) = \frac{1}{N}\sum^{N-1}_{x=0} h(x)e^{-j\frac{2\pi}{N}kx}

where:

  • NN: the number of samples
  • kk: frequency index (integer)
  • k=−N/2…N/2k = -N/2 \dots N/2
  • e−j2πNkxe^{-j\frac{2\pi}{N}kx} cycles through different frequencies, checking how much of each frequency is present

The Convolution Theorem

  1. The Fourier transform of the convolution of two functions is the same as the product of their Fourier transforms
F[g∗h]=F[g]⋅F[h]\mathcal{F}[g * h] = \mathcal{F}[g] \cdot \mathcal{F}[h]
  1. The inverse Fourier transform of the product of two Fourier transforms is the convolution of the two inverse Fourier transforms
F−1[gh]=F−1[g]∗F−1[h]\mathcal{F}^{-1}[gh] = \mathcal{F}^{-1}[g] * \mathcal{F}^{-1}[h]

Important

  • Convolution in the spatial domain is the same as the Multiplication in the frequency domain
  • FFT (Fast Fourier Transform) can convert between the spatial domain and frequency domain in O(N⋅logN)O(N \cdot logN) with NN being the number of pixels

Properties of Fourier Transform

  • Linearity
F[ax(t)+by(t)]=aF[x(t)]+bF[y(t)]\mathcal{F}[ax(t) + by(t)] = a\mathcal{F}[x(t)] + b\mathcal{F}[y(t)]
  • Fourier transform of a real signal is symmetric about the origin
  • The energy of the signal is the same as the energy of its Fourier transform
  • You don’t lose information when you convert back and forth between spatial and frequency domains

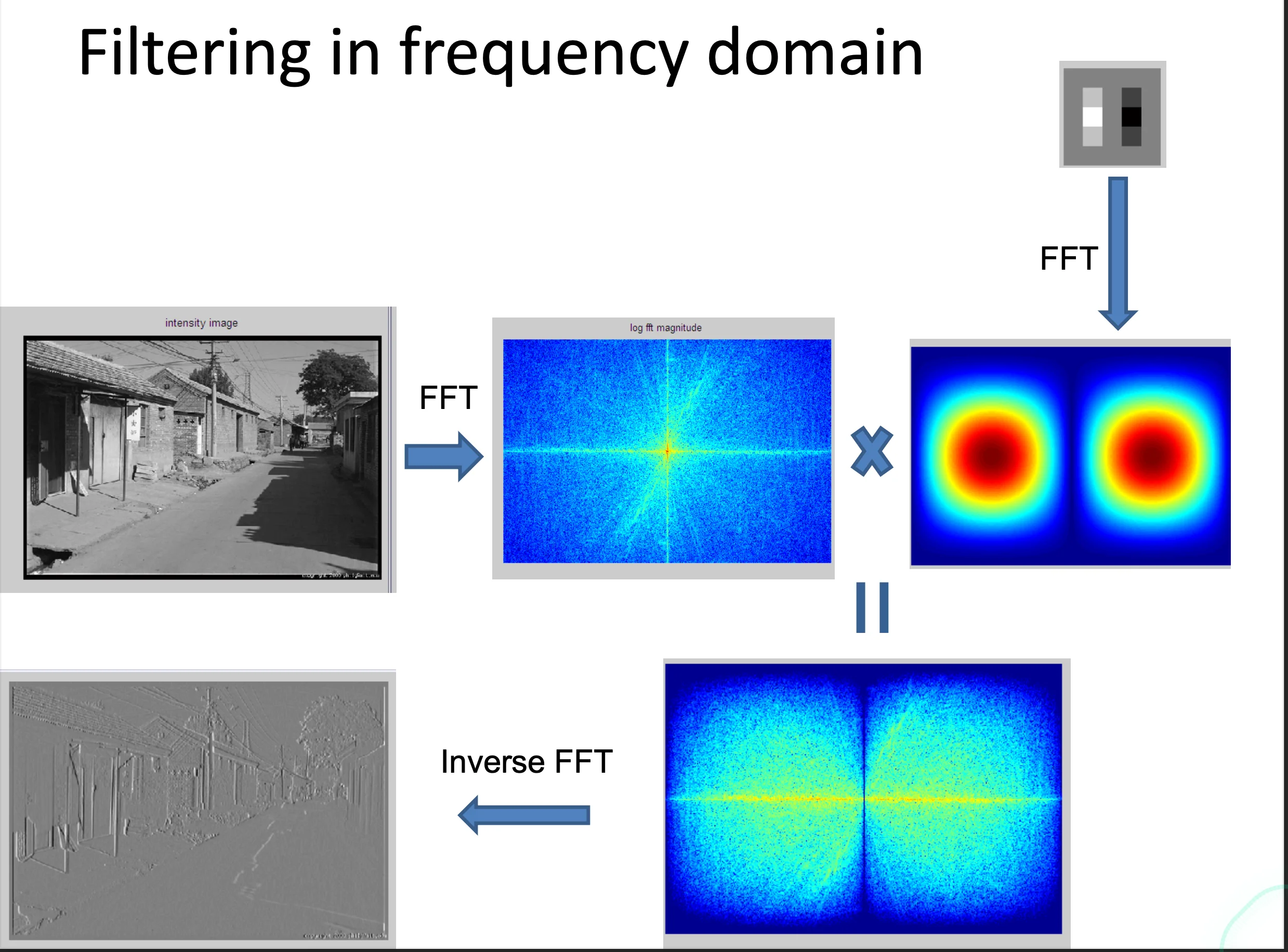
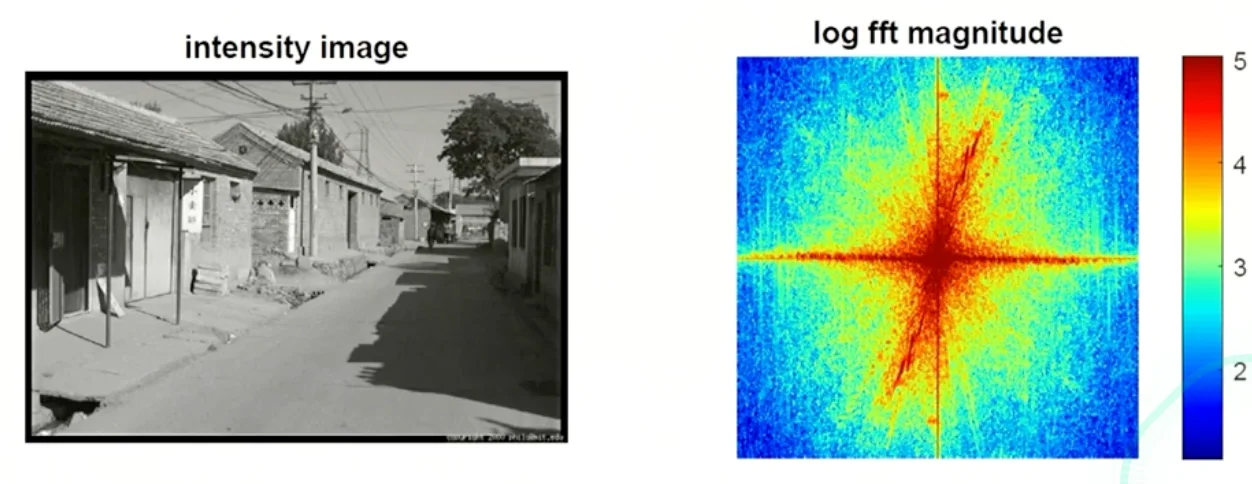
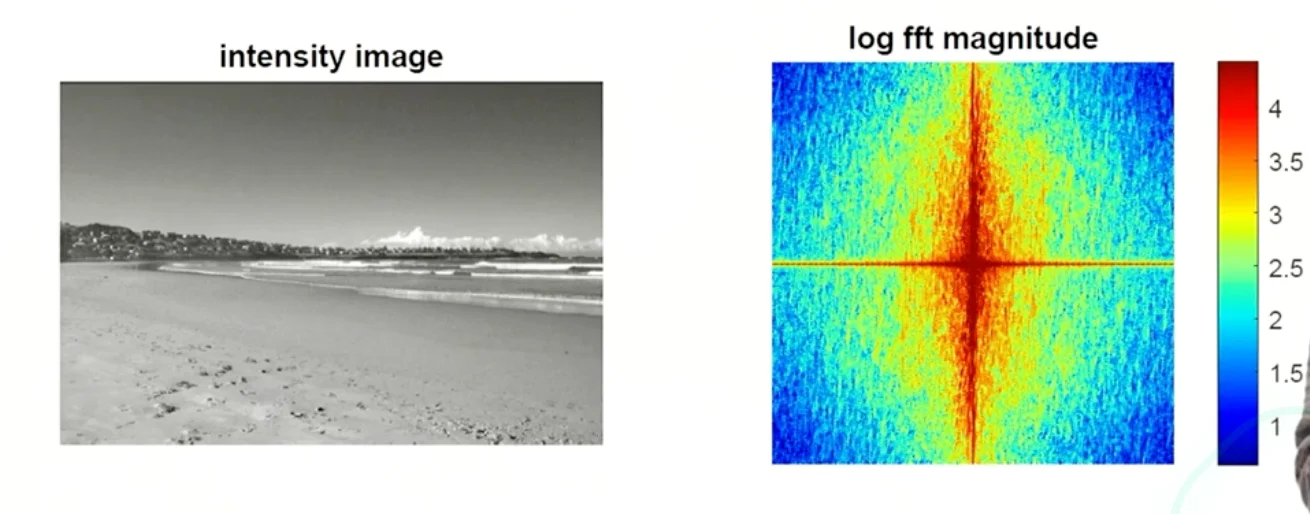
clipboard.png

Image Frequency Examples

  • Frequency →\rightarrow changes

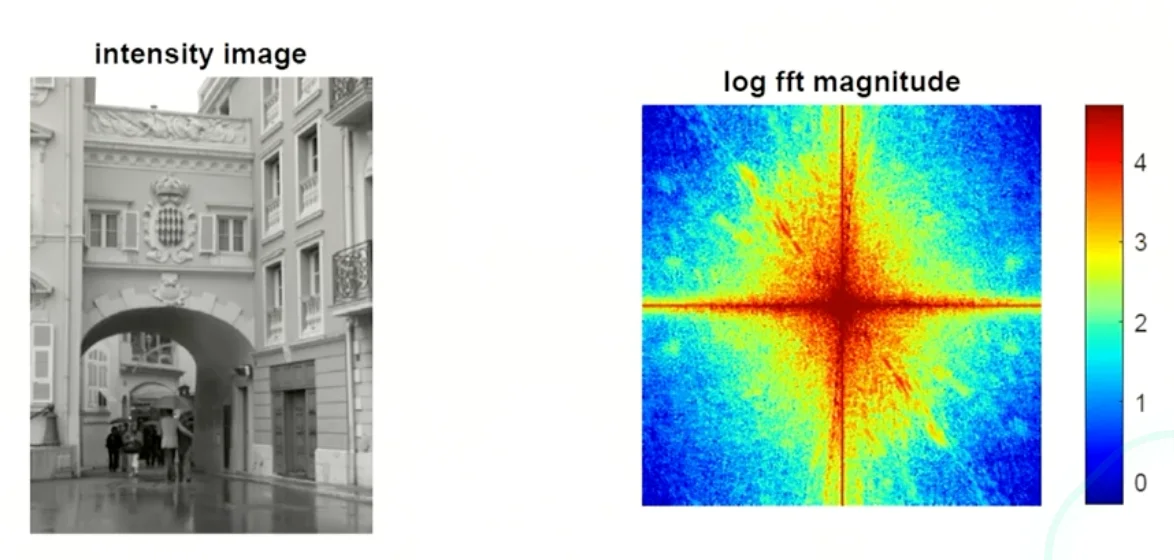
clipboard.png

  • Moving horizontally and vertically crosses a lot of edges.

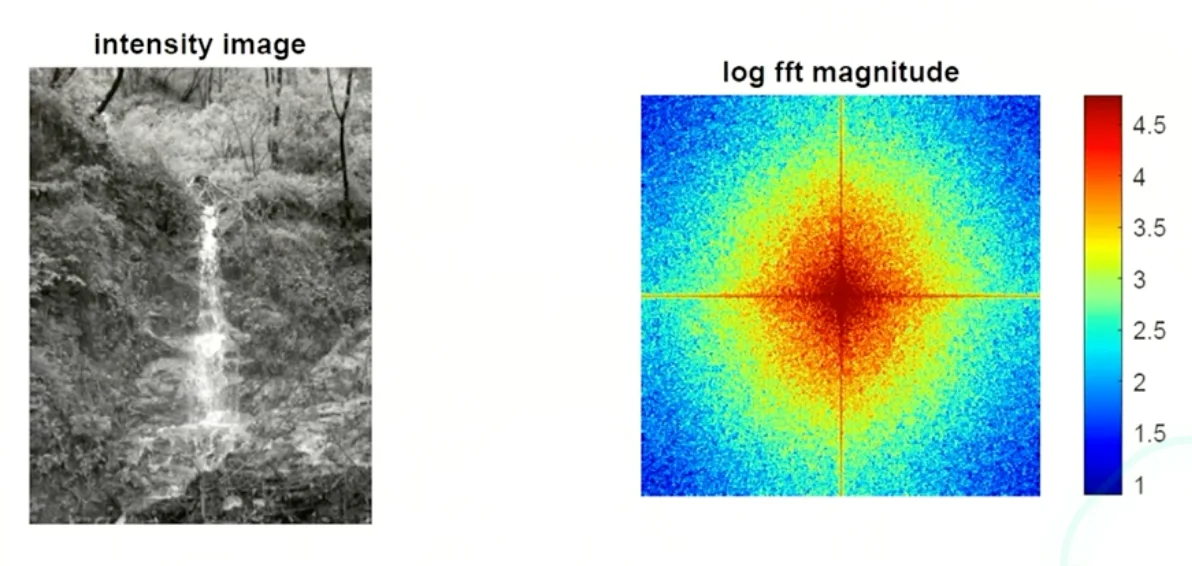
clipboard.png

  • Frequencies are spread evrywhere →\rightarrow more rounded

Note

For city images it’s more common to have star shapes, while natural images are tend to be rounded shapes.

clipboard.png clipboard.png

Comparison of filters

clipboard.png clipboard.png

  • Gaussian filter →\rightarrow selecting for lower frequencies

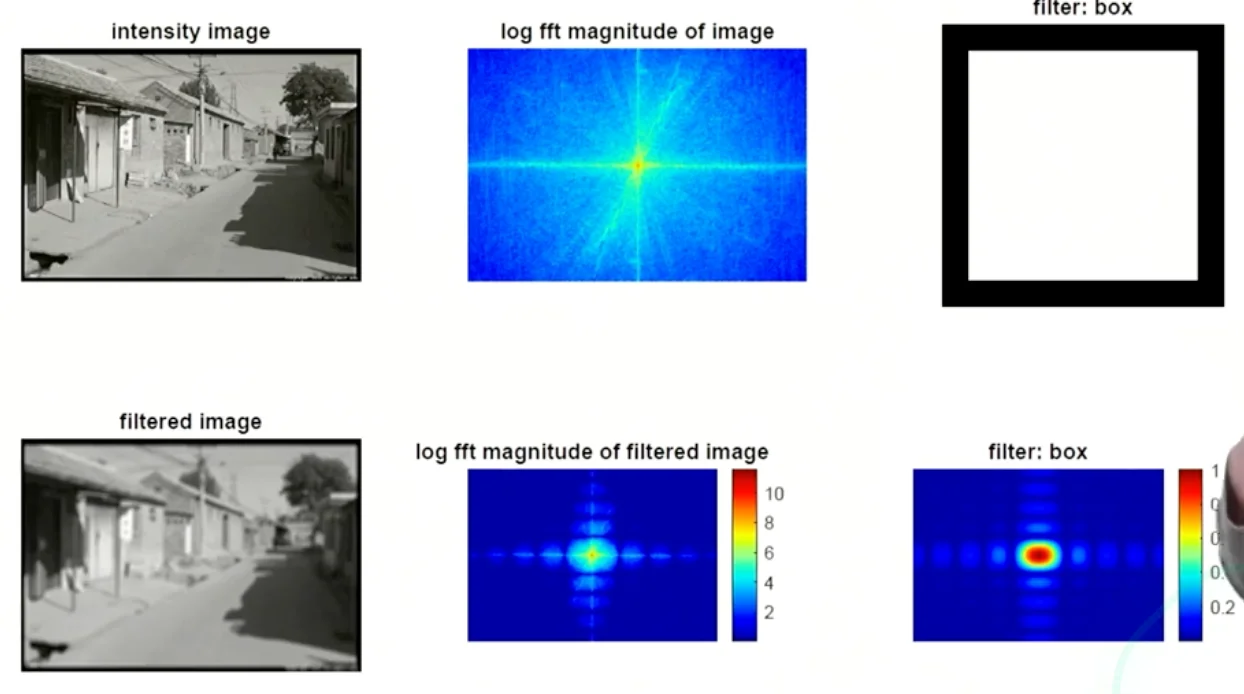
clipboard.png clipboard.png

  • Box filter:
  • preserve both low and high frequencies
  • The disjointed range of higher frequencies is also preserved, so it doesn’t prove as good of a smoothing effect as a Gaussian

Mixing Images

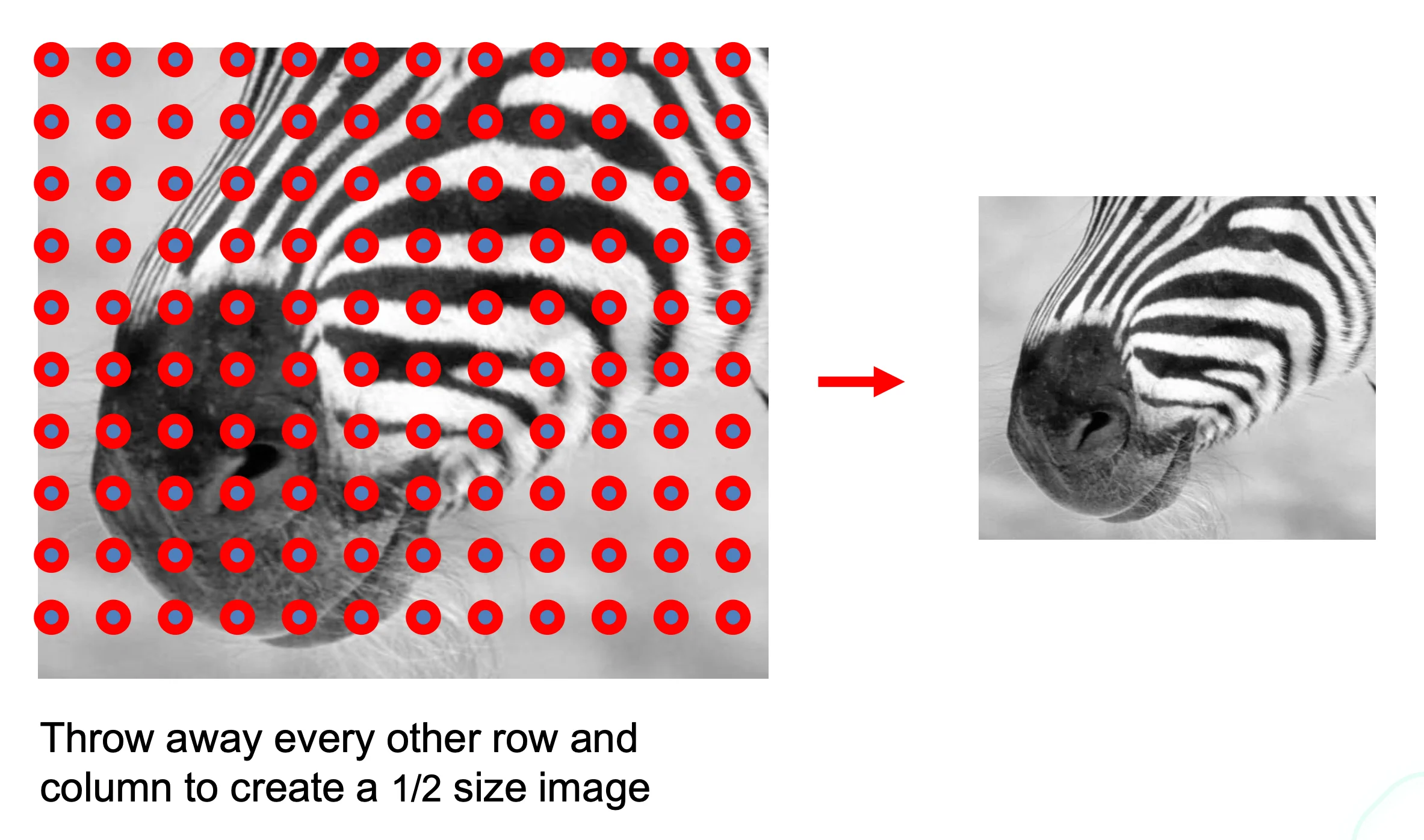
clipboard.png clipboard.png

Sampling

  • Why does a lower resolution image still make sense to use?
  • Images are typically smooth, and sampling cuts off high frequencies, which are not that many in a image
  • We can thus shrink an image without losing a lot of information

clipboard.png

Aliasing Problem

  • Sub-sampling may be dangerous as characteristic errors may appear

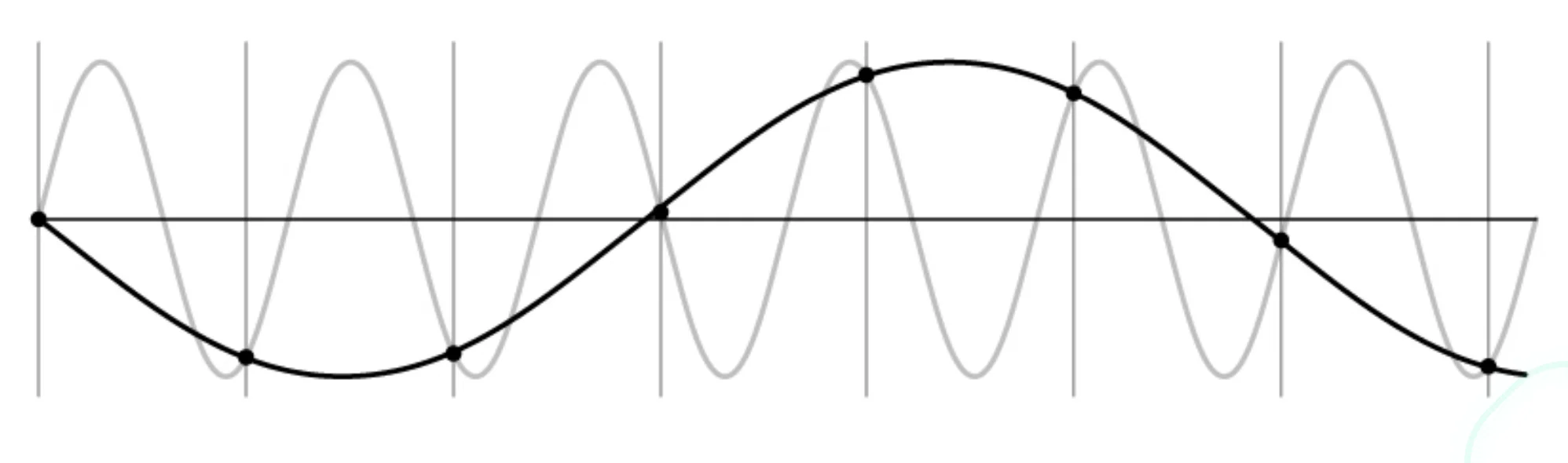
clipboard.png

  • We create an artifact that’s not in the original signal

Nyquist-Shannon Sampling Theorem

  • When sampling a signal at discrete intervals, the sampling frequency must be ≥2×fmax\ge 2 \times f_{max}
  • fmaxf{max}: max frequency of the input signal
  • This allows a reconstruction of the original image

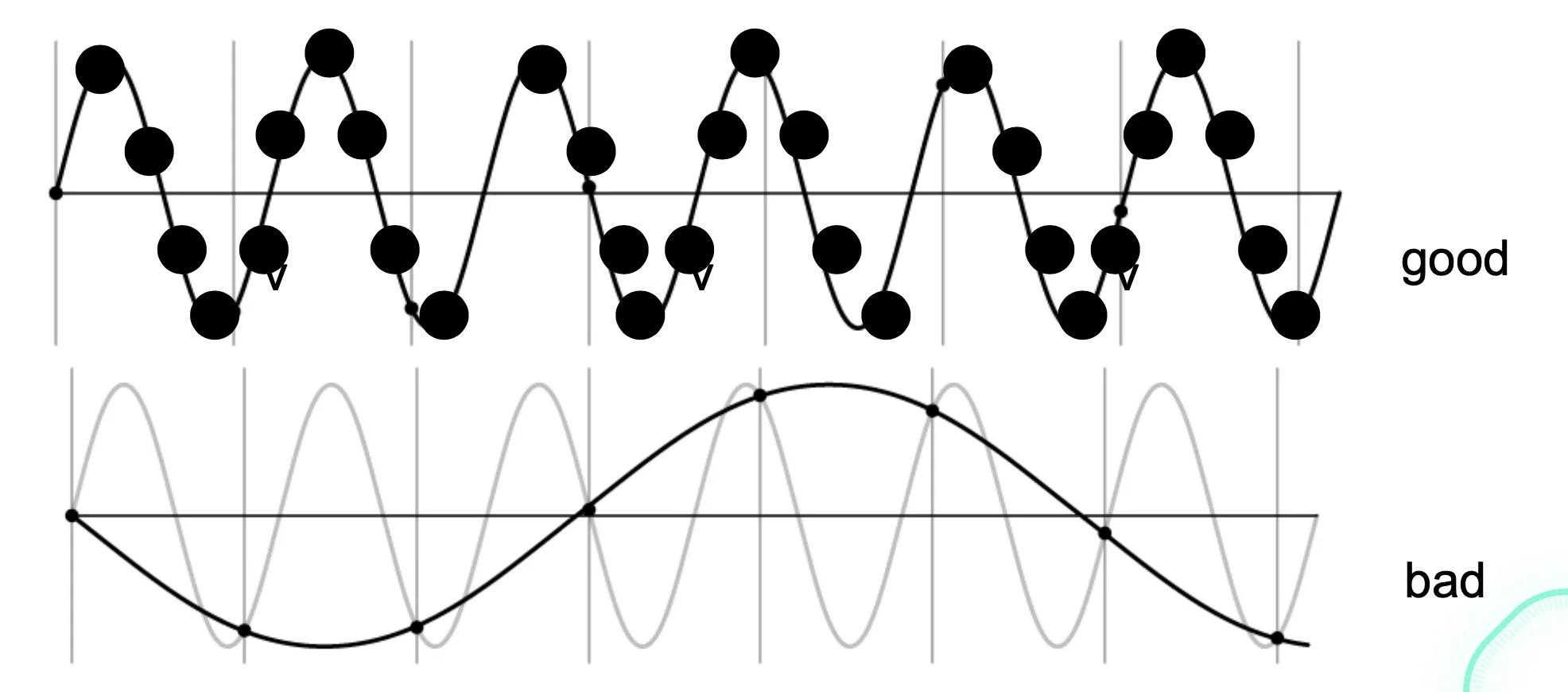
clipboard.png

Solution (Anti-aliasing)

  • Sample more often
  • Get rid of all frequencies that are greater than half of the new sampling frequencies
  • lose some high frequencies information but it’s better than aliasing
Image→⏟gaussian filterLow-pass filtered Image→⏟sampleLow-res ImageImage \underbrace\rightarrow_{\text{gaussian filter}} \text{Low-pass filtered Image} \underbrace\rightarrow_{\text{sample}} \text{Low-res Image} 
import numpy as np
from scipy.ndimage import gaussian_filter

# 1. Start with image(h, w)
# Let's assume `image` is a NumPy array of shape (h, w)

# 2. Apply low-pass filter (Gaussian blur)
im_blur = gaussian_filter(image, sigma=1) # fspecial('gaussian', 7, 1) ≈ Gaussian with σ=1

# 3. Sample every other pixel
im_small = im_blur[::2,::2]

clipboard.png

clipboard.png clipboard.png

Hybrid Image in FFT

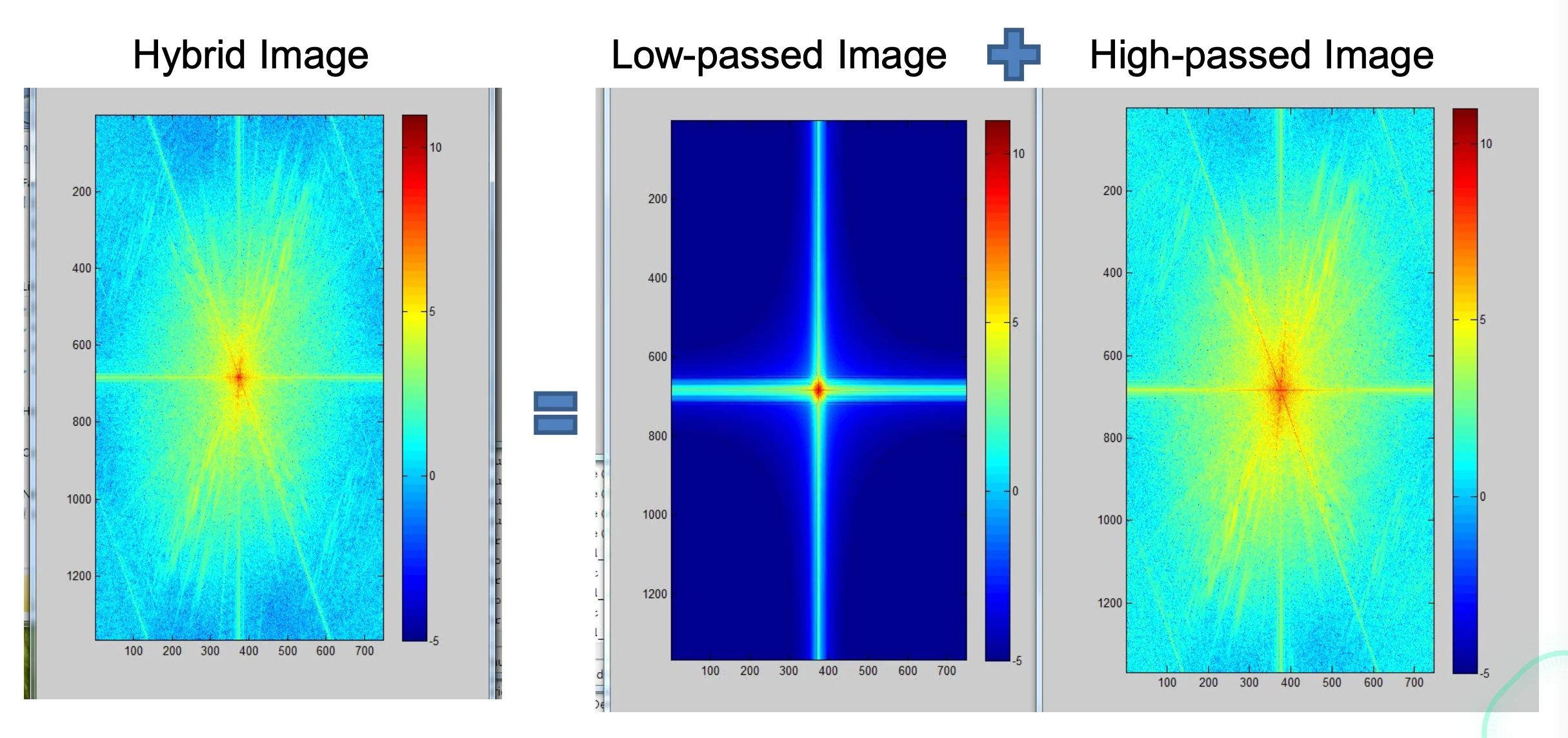
clipboard.png

  • When we’re close to the image, the higher frequencies dominate our perception, so we observe them much more readily
  • When we’re further away, high frequencies are smoothed out and we can only observe the low passed image