2.2 Template Matching

Review - Matching Frequency Plots to Images

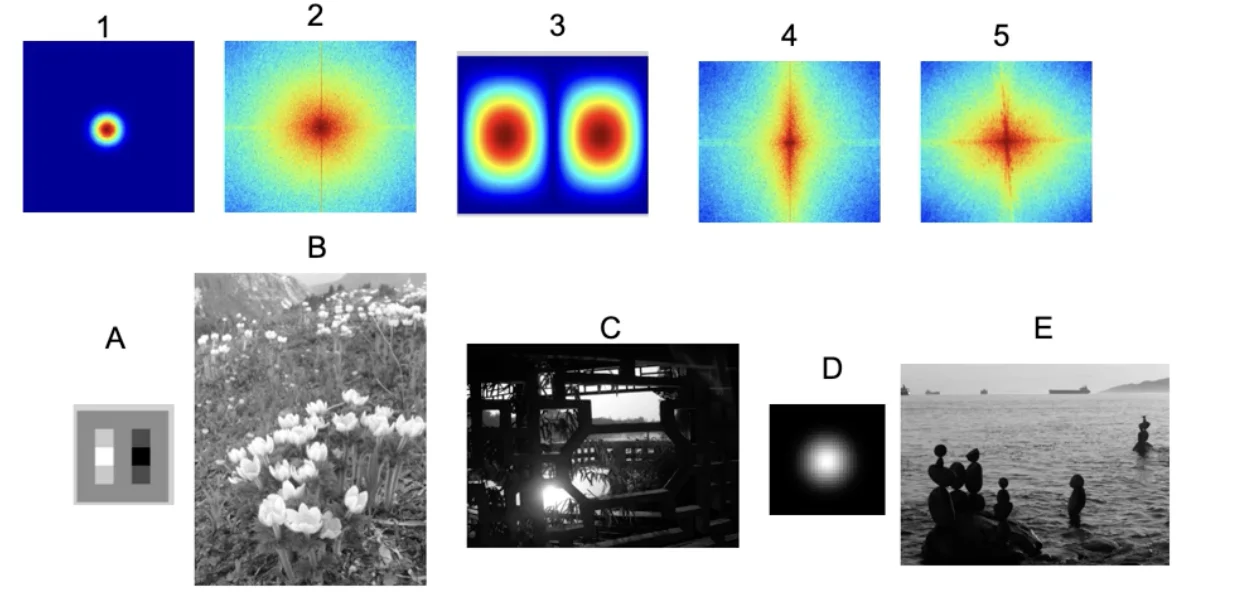
Screenshot 2025-09-08 at 09.58.09

  • 1→D1 \rightarrow D
  • 2→B2 \rightarrow B
  • 3→A3 \rightarrow A
  • 4→E4 \rightarrow E
  • A lot of horizontal edges due to the waves and due to their horizons.
  • There aren’t a lot of vertical edges
  • 5→C5 \rightarrow C

Template Matching

  • Goal: find an eye in image
  • Challenge:
  • What is a good similarity or distance measure between two patches?
  • Correlation
  • Zero-mean correlation
  • Sum Square Difference
  • Normalized Cross Correlation

Important

  • Assume the following formulas are formulated given that:
  • gg: image
  • ff: filter

∙\bullet Correlation

  • Filter the image with eye patch
h[m,n]=∑k,lg[m+k,n+l]⋅f[m,n]h[m, n] = \sum_{k, l} g[m + k, n + l] \cdot f[m, n]

clipboard.png

  • ff = image
  • gg = filter

Warning

This simply takes weighted summation over each position of the image

  • Places that are dark →\rightarrow lowest possible response
  • Places that are white →\rightarrow highest possible response

∙\bullet Zero-mean correlation

  • Simple fix for correlation
  • Instead of scanning with the direct intensity patch, we subtract the average intensity from the template
h[m,n]=∑k,l(f[k,l]−fˉ)⋅g[m+k,n+l]h[m, n] = \sum_{k, l} (f[k, l] - \bar{f}) \cdot g[m + k, n + l]

clipboard.png

  • fˉ\bar{f}: mean of f
  • If patch and templates are dark in the same places and light in the same places, you’re going to have a strong positive response.

Warning

The method only cares about whether a pixel is bright or dark in the same places, but it doesn’t take the degrees into considerations

∙\bullet Sum of Squared Difference (SSD)

h[m,n]=∑k,l(g[k,l]−f[m+k,n+l])2h[m, n] = \sum_{k, l}(g[k, l] - f[m + k, n + l])^2

clipboard.png

  1. Take the template and scan it over the image.
  2. At each position you take the difference between the corresponding pixels in the template and image patch.

Tip

SSD enforces that the intensities have to be exactly the same as the image in the template

Implement SSD with linear filter

h[m,n]=∑k,l(g[k,l]−f[m+k,n+l])2=∑k,lg[k,l]2−2g[k,l]f[m+k,n+l]+f[m+k,n+l]2=∑k,lg[k,l]2−2∑k,lg[k,l]f[m+k,n+l]+∑k,lf[m+k,n+l]2=∑k,lg[k,l]2⏟constant−2filter(f,g)⏟Linear Filter+filter(f2,ones(g.shape))⏟Element wise squared f\begin{align*} h[m, n] &= \sum_{k, l}(g[k, l] - f[m + k, n + l])^2 \\ &= \sum_{k, l} g[k, l]^2 - 2g[k,l]f[m + k, n + l] + f[m + k, n+ l]^2 \\ &= \sum_{k, l} g[k, l]^2 - 2 \sum_{k, l} g[k,l]f[m + k, n + l] + \sum_{k, l}f[m + k, n+ l]^2 \\ &\begin{align*} = \underbrace{\sum_{k, l} g[k, l]^2}_{\text{constant}} - 2 \underbrace{filter(f, g)}_{\text{Linear Filter}} + \underbrace{filter(f^2, ones(g.shape))}_{\text{Element wise squared f}} \end{align*} \end{align*}

Warning

  • SSD requires you have the exact matching of intensities.
  • The change of contrast would lead to the Failure of template matching

clipboard.png

∙\bullet Normalized Cross-correlation

h[m,n]=∑k,l(g[k,l]−gˉ⏞mean template)(f[m+k,n+l]−fˉm,n⏞mean image patch)∑k,l(g[k,l]−gˉ)2(f[m+k,n+l]−fˉm,n)2⏟The standard deviation of the template and the patchh[m, n] = \frac{ \sum_{k, l} (g[k, l] - \overbrace{\bar{g}}^{\text{mean template}}) (f[m + k, n + l] - \overbrace{\bar{f}_{m, n}}^{\text{mean image patch}}) }{ \underbrace{\sqrt{\sum_{k, l} (g[k, l] - \bar{g})^2 (f[m + k, n + l] - \bar{f}_{m, n})^2}}_{\text{The standard deviation of the template and the patch}} }
  • By doing this, the multiplicative factor induced by image scaling will be cancelled out by the standard deviation.

Tip

  • You can also do a simple cross-correlation without normalizing it (not dividing standard deviation).
  • This works when you only care about the issues related to the shifts of intensity without dealing with the contrast and multiplications of intensity

Without Scaling

clipboard.png

With Scaling

clipboard.png

Tip

All these template matching methods are implemented with cv2.matchTemplate(im, template, cv2.TM_CCOEFF_NORMED) with the difference of the third argument.

Summary of Different Matching Filter

  • Zero-mean filter: Fastest but not a great matcher
  • SSD: Next fastest, sensitive to overall intensity
  • Normalized coss-correlation: Slowest, invariant to local average intensity and contrast

Sampling

Gaussian Pyramid

  • Repeatly perform Image -(Gaussian Filter)-> Low-pass Filtered Image -(Sample)-> Low-Res Image

clipboard.png

Laplacian pyramid

clipboard.png

∙\bullet Laplacian Filter

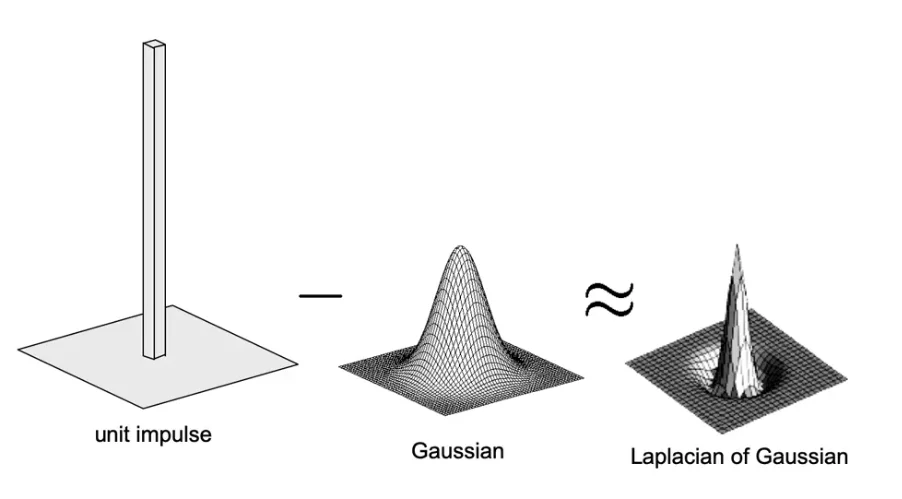
clipboard.png

Computation Process

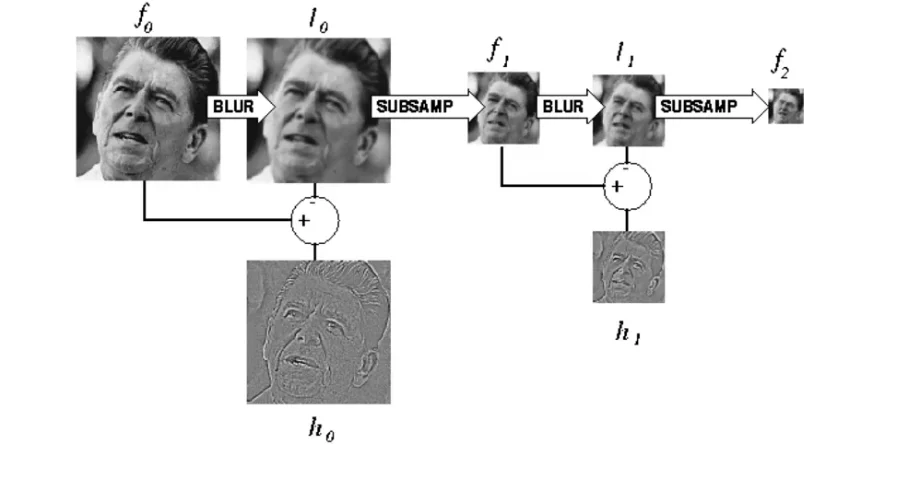
clipboard.png

  1. Apply Gaussian filter to the image
  2. Subtract the smoothed images from the original image
  3. Down-sample

Warning

You can reconstruct the image from Laplacian pyramid but you may lose some information

Lossless Reconstruction

∙\bullet Original Process

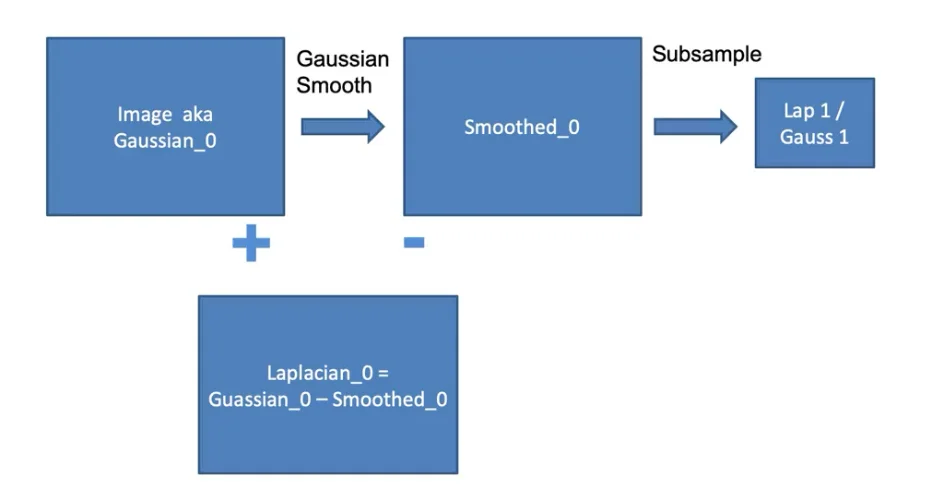
clipboard.png

∙\bullet A small tweak

  • Instead of just smoothing and subtracting the smoothed from the original, we:
  1. Compute the Lap1
  2. up-sample it
  3. smooth it
  4. subtract that result from the image to get the top level of a Laplacian pyramid

Hybrid Image in Laplacian Pyramid

clipboard.png

  • In the high frequency, only the cat is visible (Laplacian Smoothing)
  • In low frequency, humans are more visible (Gaussian Smoothing)

Coarse-to-Fine Search

1. Start at the coarsest pyramid level

  • Search the full range of translations
  • Find the best translation (txL,tyL)(t^L_x, t^L_y)

2. Upsample the estimate when moving to the next finer level

(txL−1,tyL−1)≈(2txL,2txt)(t^{L-1}_x, t^{L-1}_y) \approx (2t^{L}_x, 2t^{t}_x)

Note

Image size doubles between levels

3. Local Refinement

  • Instead of searching the full range again, only serach a small window:
tx∈[2txL−s,2txL+s]ty∈[2tyL−s,2txL+s]t_x \in [2t^L_x - s, 2t^L_x + s] \\ t_y \in [2t^L_y - s, 2t^L_x + s] \\

4. Repeat until reaching the original resolution

Image Registration

Aligning two images of the same scene so that corresponding points overlap

I2(x,y)→I2(x−tx,y−ty)I_2(x, y) \rightarrow I_2(x -t_x, y -t_y)

where:

  • (tx,ty)(t_x, t_y) is the translation vector we want to estimate.

Image Pyramid

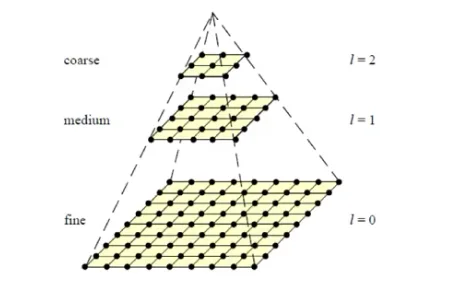
clipboard.png

  • Build an image pyramid
  • level 0: full-resolution image, size H×WH\times W
  • level 1: downsampled by factor 2→H2×W22 \rightarrow \frac{H}{2} \times \frac{W}{2}
  • level 2: downsampled by again →H4×W4\rightarrow \frac{H}{4} \times \frac{W}{4}
  • This gives progressively smaller, blurrier images that retain coarse structure but lose higyh-frequency detail

Sum of Squared Difference (SSD) Matching

Evaluate how well two images align under translation

SSD(tx,ty)=∑x,y(I1(x,y)−I2(x−tx,y−ty))2SSD(t_x, t_y) = \sum_{x, y}(I_1(x, y) - I_2(x - t_x, y - t_y))^2
  • Compute SSD for each candidate translation (tx,ty)(t_x, t_y) from coarse to fine
(tx∗,ty∗)=arg min⁡tx,tySSD(tx,ty)(t^*_x, t^*_y) = \argmin_{t_x, t_y}SSD(t_x, t_y)
  • Choose the translation that minimizes SSDSSD

Tip

Corase-to-fine image registration is faster to compute as at each coarse level, images are much smaller and there are few pixels to compare.

Caution

  • Not Guaranteed Optimal
  • If the corase-level images lose too much detail, the algorithm may converge to the wrong translation.
  • Works in practice
  • Meaningful structure is in low frequencies
  • Noice is reduced at coarse scales
  • Danger
  • Overly downsampling may lead to the inability to align images correctly