2.3 Denoising, Compression

Image Alignment with FFT

  • FFTFFT can be used to efficiently implement SSDSSD

∙\bullet Recap of Convolution Theorem

f∗g=F−1{{f}⋅F{g}}f * g = \mathcal{F}^{-1}\{\mathcal\{f\} \cdot \mathcal{F}\{g\}\}
  • f∗gf * g: convolution in the spatial domain
  • F−1{{f}⋅F{g}}\mathcal{F}^{-1}\{\mathcal\{f\} \cdot \mathcal{F}\{g\}\}:Fourier transform in the frequency domain

∙\bullet SSD Implementatioon with FFT

Standard SSD Formula:

SSD(u,v)=∑x,y[I(x,y)−T(x−u,y−v)]2=∑x,yI2(x,y)+∑x,yT2(x−u,y−v)−2∑x,yI(x,y)T(x−u,y−v)=∑x,yI2(x,y)+∑x,yT2(x−u,y−v)−2(I∗T)=∑x,yI2(x,y)+∑x,yT2(x−u,y−v)−2(F−1{{f}⋅F{g}})\begin{align*} SSD(u, v) &= \sum_{x, y}[I(x, y) - T(x - u, y - v)]^2 \\ &= \sum_{x, y} I^2(x, y) + \sum_{x, y} T^2(x - u, y - v) - 2\sum_{x, y} I(x, y)T(x - u, y - v) \\ &= \sum_{x, y} I^2(x, y) + \sum_{x, y} T^2(x - u, y - v) - 2(I * T)\\ &= \sum_{x, y} I^2(x, y) + \sum_{x, y} T^2(x - u, y - v) - 2(\mathcal{F}^{-1}\{\mathcal\{f\} \cdot \mathcal{F}\{g\}\})\\ \end{align*}
  • I(x,y)I(x, y): The larget image or scene in which you’re searching
  • T(x,y)T(x, y): The smaller image patch or pattern that you’re finding
  • (u,v)(u,v): The offset from the original position

[!IMPORTANT] > Computational Complexity

  • Spatial Domain SSD: O(MN⋅WH)O(MN \cdot WH)
  • (M,N)(M, N) is image size
  • (W,H)(W, H) is template size
  • FFT-based SSD
  • O(MN⋅log(MN))O(MN \cdot log(MN))

Image Compression Principle

  • Most intensity information is concentrated in lower frequencies

JPEG Compression (lossy)

  • JPEG is a lossy compression method that exploits the human visual system’s reduced sensitivityto high-frequency changes and chrominance variations

1. Color Space Conversion

  • Convert RGBRGB to YCbCrYC_b C_r
Y=0.299R+0.587G+0.114BCb=−0.168R−0.331G+0.500B+128Cr=0.500R−0.419G−0.081B+128\begin{align*} Y &= 0.299R+0.587G+0.114B \\ C_b &= −0.168R−0.331G+0.500B+128 \\ C_r&=0.500R−0.419G−0.081B+128 \end{align*}

2. Sub sample Chroma by factor of 2

  • Subsample CbC_b and CrC_r channels by factor of 2
  • People are not sensitive to color

3. Block Decomposition

  • Divide each channel into 8×88 \times 8 pixel blocks
  • Subtract 128 from each pixel (center around 0 for better compression)

4. Discrete Cosine Transform (DCT)

F(u,v)=14C(u)C(v)∑x=07∑y=07cos[(2x+1)uπ16]cos[(2y+1)vπ16]F(u, v) = \frac{1}{4} C(u)C(v)\sum_{x=0}^7 \sum_{y=0}^7 cos[\frac{(2x + 1)u\pi}{16}] cos[\frac{(2y + 1)v\pi}{16}]
  • (0,0)(0, 0): DC component (average intensity)
  • (0,7)(0, 7): Highest horizontal frequency
  • (7,0)(7, 0): Highest vertical frequency
  • (7,7)(7, 7): Highest diagonal frequency

where:

C(u)={12if u=01otherwiseC(u) = \begin{cases} \frac{1}{\sqrt{2}} & \text{if } u = 0 \\ 1 & \text{otherwise} \end{cases}

5. Quantization

Q(u,v)=round(F(u,v)q(u,v))Q(u, v) = round(\frac{F(u, v)}{q(u, v)})
  • q(u,v)q(u, v) is the quantization table value at position (u,v)(u, v)
  • A typical quantization table:
16 11 10 16 24 40 51 61
12 12 14 19 26 58 60 55
14 13 16 24 40 57 69 56
14 17 22 29 51 87 80 62
18 22 37 56 68 109 103 77
24 35 55 64 81 104 113 92
49 64 78 87 103 121 120 101
72 92 95 98 112 100 103 99

6. Entropy Encoding

  • Use Huffman coding to encode quantized coefficients
  • Zigzag scanning to group zeros together
  • Run-length encoding for sequences of zeros

JPEG Reconstruction

1. Dequantization

F^(u,v)=Q(u,v)×q(u,v)\hat{F}(u, v) = Q(u, v) \times q(u, v)

2. Inverse DCT

f^(x,y)=14∑u=07∑v=07C(u)C(v)F^(u,v)cos[(2x+1)uπ16]cos[(2y+1)vπ16]\hat{f}(x, y) = \frac{1}{4}\sum^7_{u = 0}\sum^7_{v =0} C(u)C(v)\hat{F}(u, v)cos[\frac{(2x+ 1)u\pi}{16}] cos[\frac{(2y + 1)v\pi}{16}]

Caution

JPEG Artifacts

  • Blcoking: 8x8 block boundaries become visible at high compression
  • Ringing: Oscillations near sharp edges due to quantization of high frequencies
  • Color bleeding: Chroma subsampling causes color information to spread

PNG (Lossless)

  1. Predict that a pixel’s value based on its upper-left neighborhood
  2. Store difference of predicted and actual value
  3. Pkzip it (DEFLATE Algorithm)

Important

  • PNG exploits image smoothness by predicting each pixel from its neighbors and storing ONLY the prediction errors.
  • It’s the best for images with few colors, sharp edges, text, graphics

Denoising

Reducing Gaussian Noises

  • Smooth out the noises by applying Gaussian filter

clipboard.png

Caution

Gaussian filtering may induce salt-and-pepper Noises

Screenshot 2025-09-10 at 19.46.14

Median Filtering

  • Median filtering is robust to outliers

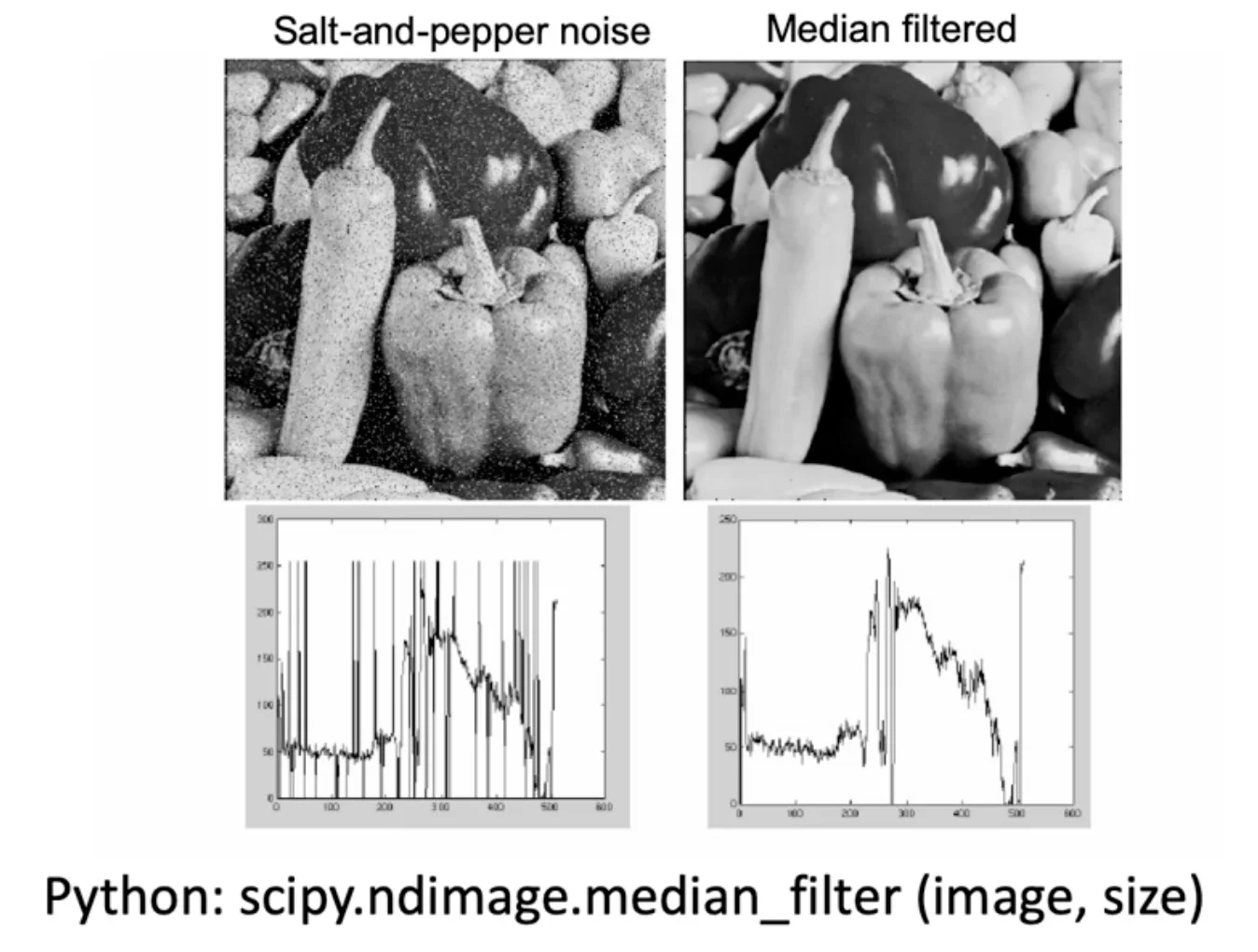
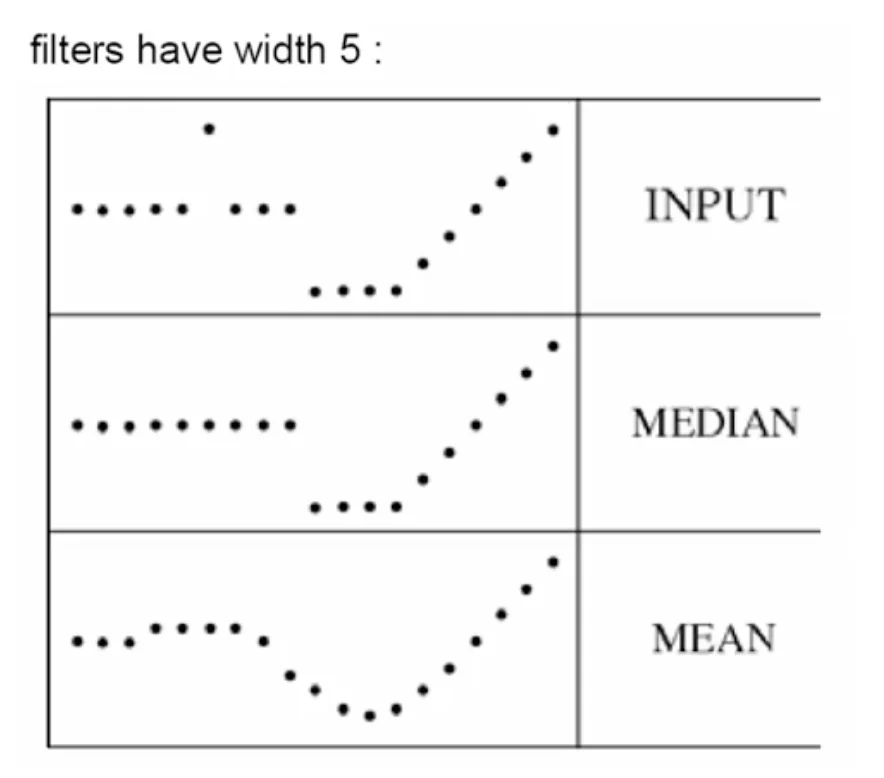
clipboard.png Screenshot 2025-09-10 at 19.47.48

Median vs Gaussian

clipboard.png

Bilateral Filtering (weight by spatial distance and intensity difference)

clipboard.png