3.2.3 Histogram Equalization

Histogram Equalization

  • Reassign values so that the number of pixels with each values is more evenly distributed

Histogram

  • a count of how many pixels with the same value
hi=∑j∈pixels1(pj=i)h_i = \sum_{j \in pixels} 1 (p_j = i)

Cumulative histogram

  • a count of number of pixels less than or equal to each value
ci=ci−1+hic_i = c_{i - 1} + h_i

Example

Screenshot 2025-10-10 at 10.40.56

Histogram Equalization

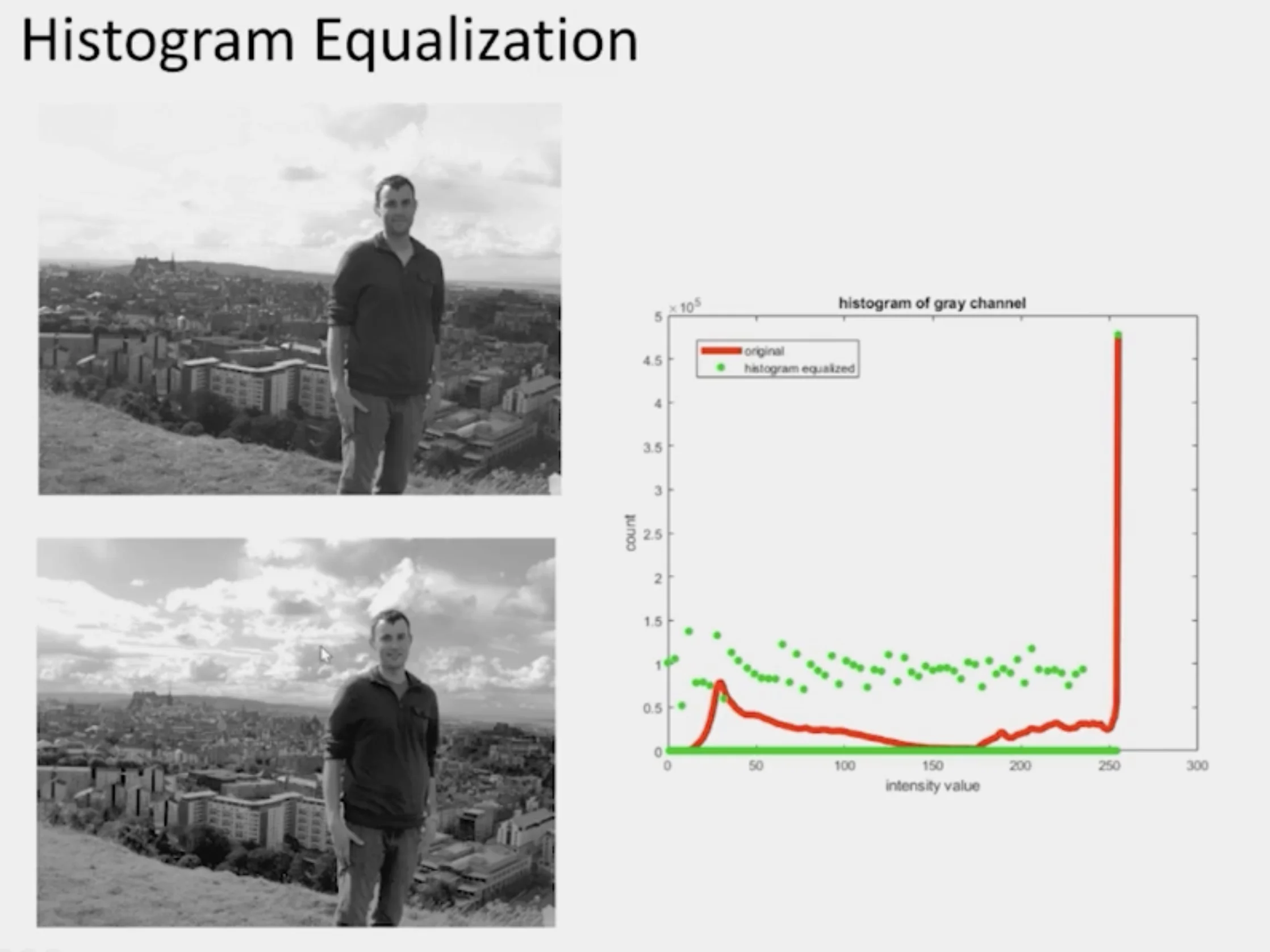
clipboard.png

  • The original intensity is culstered on the left and right sides.
  • After the equalization, the values are more evenly distributed.

Algorithm

  • Given image with pixel values 0≤pi≤255,j=0…N0 \le p_i \le 255, j = 0\dots N
  1. Compute cumulative histogram
h(i)=∑j∈pixels1(pj=i)c(i)=c(i−1)+h(i)h(i) = \sum_{j \in pixels} 1(p_j = i) \\ c(i) = c(i - 1) + h(i)
  1. Blends between original image and image with equalized histogram
f(i)=αc(i)N⋅255+(1−α)⋅if(i) = \alpha \frac{c(i)}{N} \cdot 255 + (1 - \alpha) \cdot i
  • α:\alpha: balancing factor
  • c(i)N:\frac{c(i)}{N}: the percentile of the pixel

Locally weighted histograms

  • Compute cumulative histograms in non-overlapping M x M grid
  • For each pixel, interpolate between the histograms from the four nearest grid cells

Screenshot 2025-10-10 at 10.57.14

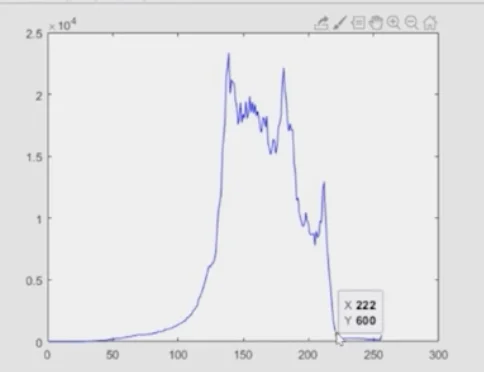
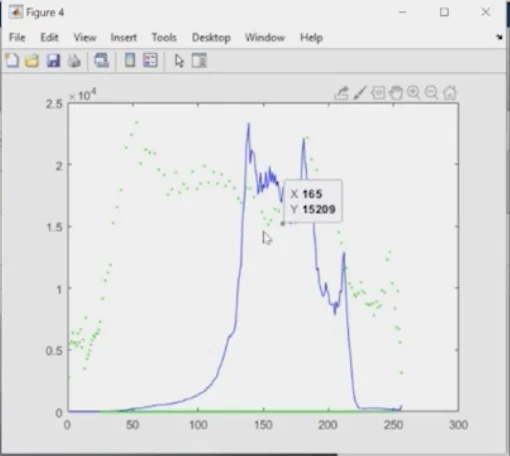
Screenshot 2025-10-10 at 10.58.55 Screenshot 2025-10-10 at 11.04.49

  • The green dots show the result of the equalization without using the original value

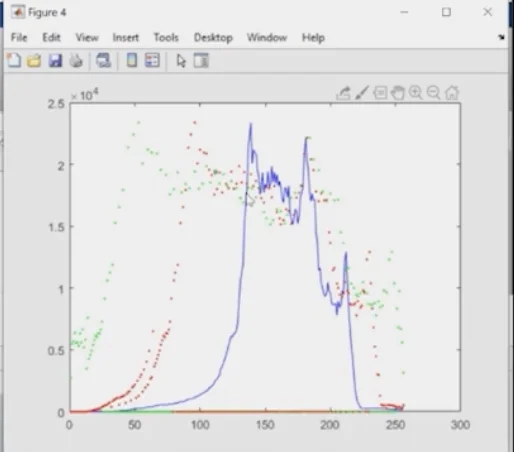
Screenshot 2025-10-10 at 11.06.39

  • The red dots show the result of the equalization using the original value

Caution

Gamma adjustment would not be great in this case, cuz we need to stretch the image out