4.2.3: Graph Cut-Based Segmentation

GrabCut

clipboard.png

  • Good region is similar to foreground color model and dissimilar from background color

Algorithm

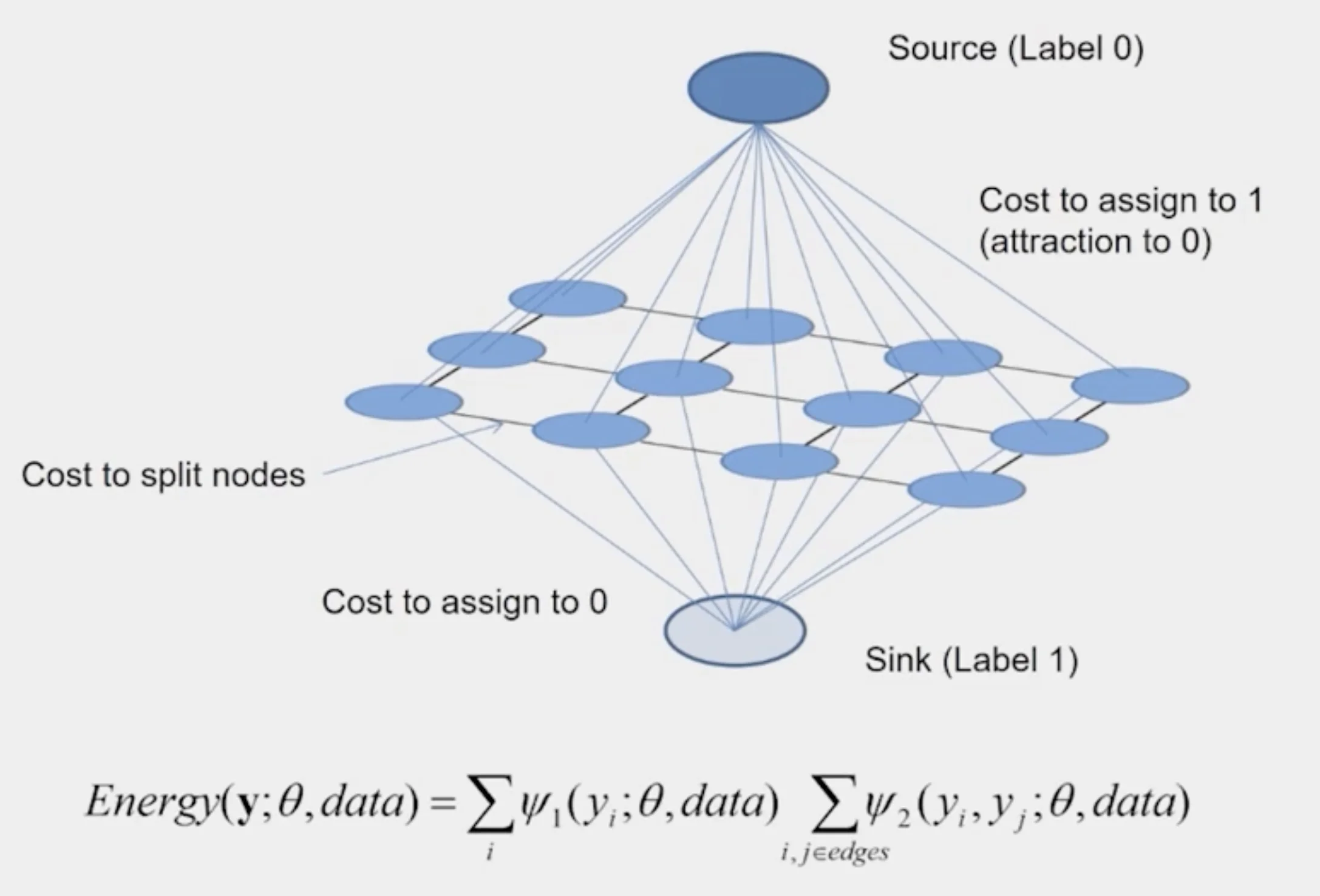
1. Define the graph

  • each pixel in the image is a node in the graph.
  • Local pixel relationship
  • nodes are connected to their neighbors
  • usually 4-connected or 8-connected
  • Two additional nodes
  • source (foreground)
  • sink (background)

2. Set weights to foreground/background (unary potentials)

  • Assign weights to pixels to measure how likely it belongs to foreground or background
  • can be modeled color histograms or mixtures of Gaussians for both regions
  • The unary potential is defined as:
unary_potentials(x)=−log⁡P(c(x);θforeground)P(c(x);θbackground)unary\_potentials(x) = -\log \frac{P(c(x); \theta_{foreground})}{P(c(x); \theta_{background})}

3. Set weights for edges between pixels (pairwise potentials)

  • Edges connect neighboring pixels. The weight reflects how similar two neighboring pixels are:
edge_potential(x,y)=k1+k2exp⁡(−∣∣c(x)−c(y)∣∣22σ2)edge\_potential(x, y) = k_1 + k_2 \exp\left(-\frac{\mid\mid c(x) - c(y) \mid\mid^2}{2 \sigma^2}\right)

4. Apply the min-cut/max-flow algorithm

  • Find the minimum ct that separates the graph into source and sink with minimal total cost

5. Iteratve till convergence

Limitations of Graph Cuts

  • Requires associative graphs
  • Connected nodes should be assigned to the same label
  • Only optimal for binary problems

Summary of Ideas

  • Pixels are nodes
  • Between-pixel edge weights based on gradients
  • Sometimes per-pixel weights for affinity to foreground/background
  • Good boundaries are a short path through the graph
  • Good regions are produced by a low-cost cut

Take-home questions

1. What would be the result in “Intelligent Scissors” if all of the edge costs were set to 1

  • The shortest path would be the shortest manhattan distance

2. How could you change boundary costs for graph cuts to work better for objects with many thin parts?

  • Think about how to modify that cost to set K1 and K2 if there are a lot of thin structures
  • Set the component penalizing the change of the labels to 0
  • This way, for the high contrast, you will not be paying the high cost
  • Apply a general cost to all the boundary so the boundary cost would not grow