5.1 Image Compositing

Feathering

Problems of simple cut and paste

  • small segmentation errors noticeable
  • pixels are too blocky
  • won’t work for semi-transparent materials

Solution

  • Near object boundary pixel values come partly from foreground, and partly from background

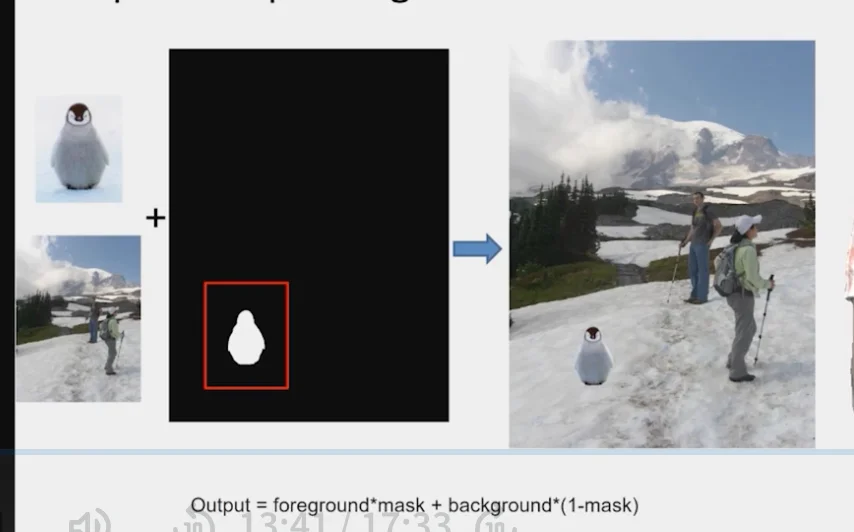
clipboard.png

Output=foreground×mask+background(1−mask)Output = foreground \times mask + background(1 - mask)

Alpha Blending/Feathering

Iblend=αIleft+(1−α)IrightI_{blend} = \alpha I_{left} + (1 - \alpha) I_{right}

Too much feathering

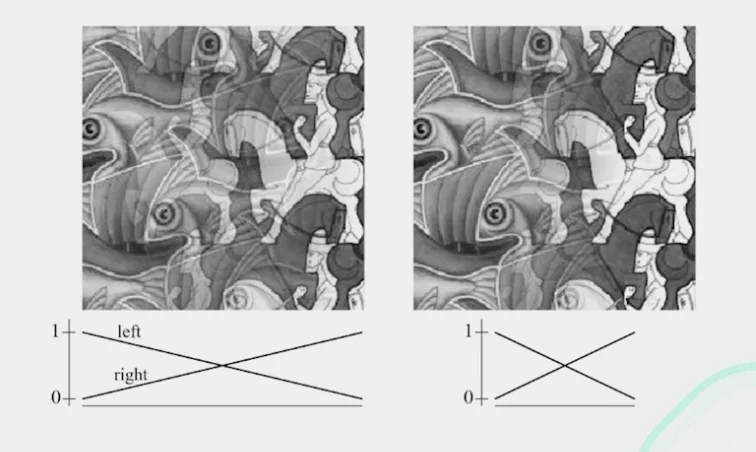
clipboard.png

  • ghosting

Too little feathering

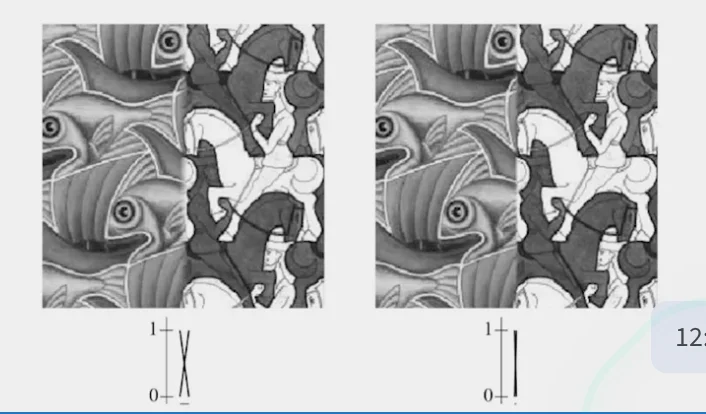
clipboard.png

  • visible boundary

Pyramid Blending

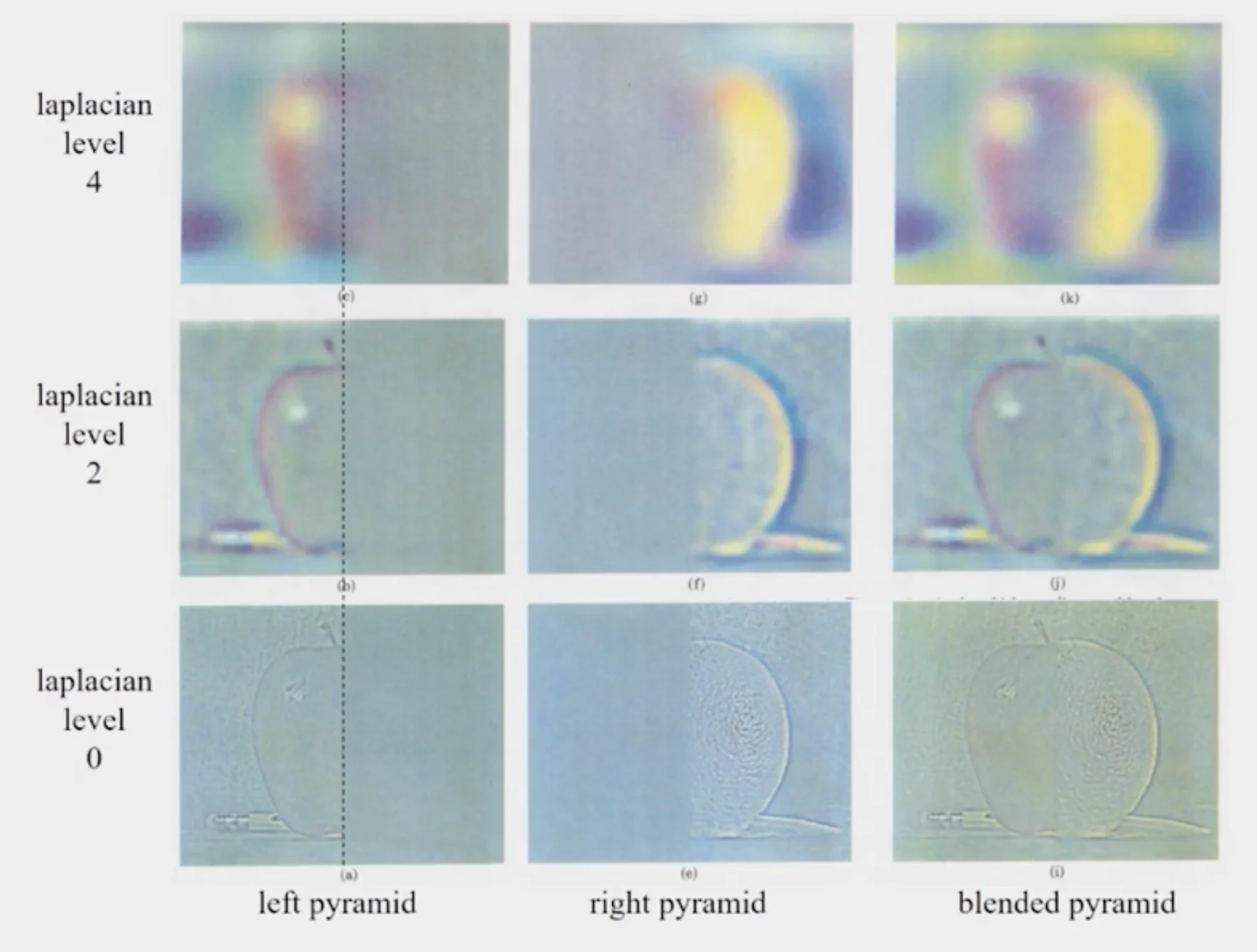
clipboard.png

Laplacian Pyramid Blending

  1. Build Laplacian pyramids for each image
  2. Build a Gaussian pyramid of region mask
  3. Blend each level of pyramid using region mask from the same level
Ll2i=L1i⋅Ri+L2i⋅(1−Ri)L_{l2}^i = L_1^i \cdot R^i + L_2^i \cdot (1 - R^i)
  1. Collapse the pyramid to get the final blended image

Poisson Blending

  • A good blend should preserve gradients of source region without changing the background
  • Treat pixxels as variables to be solved
  • Minimize squared difference between gradients of foreground and target regions
  • Keep background pixels constant
v=arg min⁡v∑i∈S,j∈Ni,∩S((vi−vj)−(si−sj))2+∑i∈,j∈,∩¬S((vi−tj)−(si−sj))2v = \argmin_v \sum_{i \in S, j \in N_i, \cap S} ((v_i - v_j) - (s_i - s_j))^2 + \sum_{i\in,j\in,\cap \neg S} ((v_i - t_j) - (s_i - s_j))^2

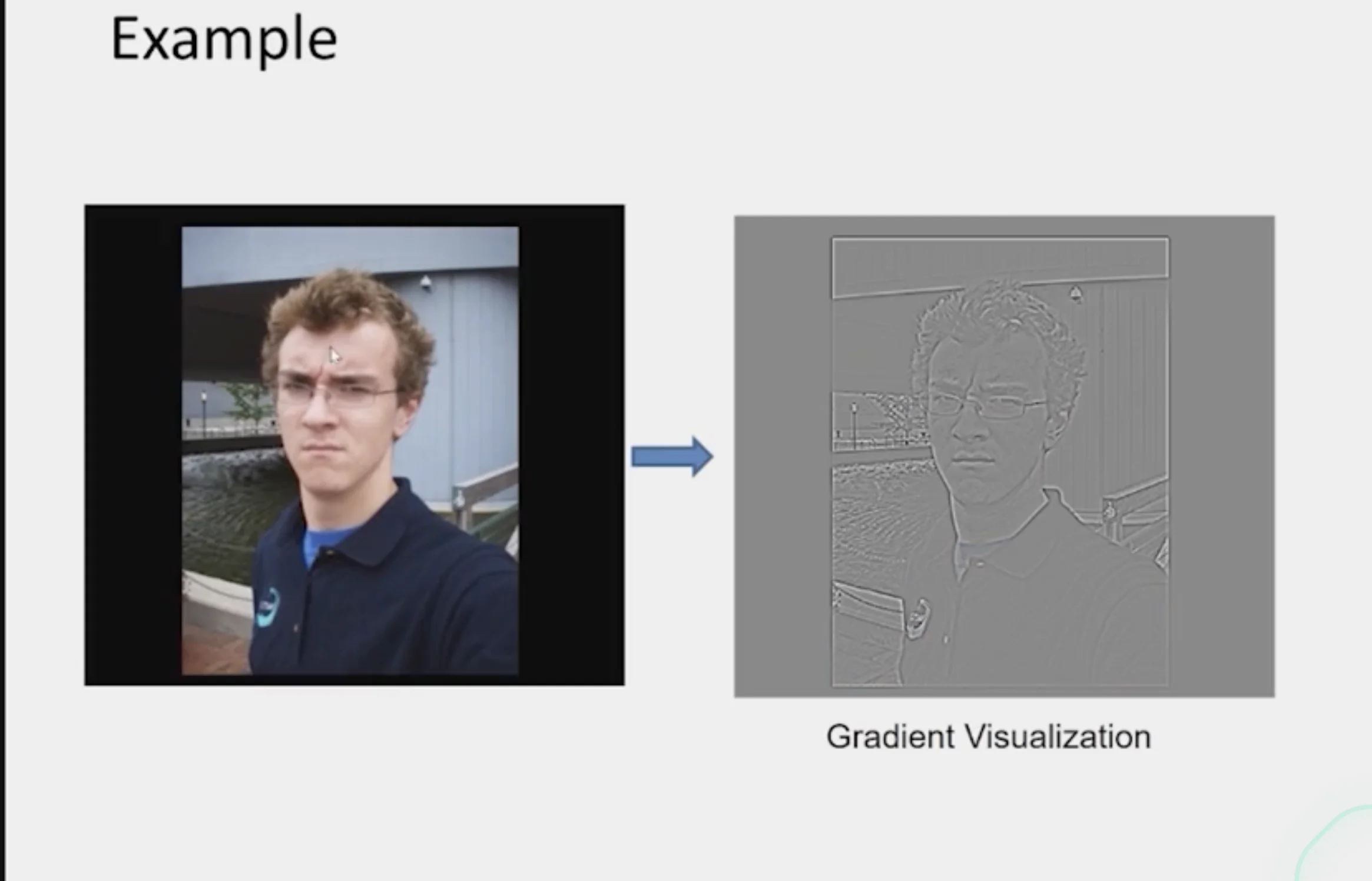
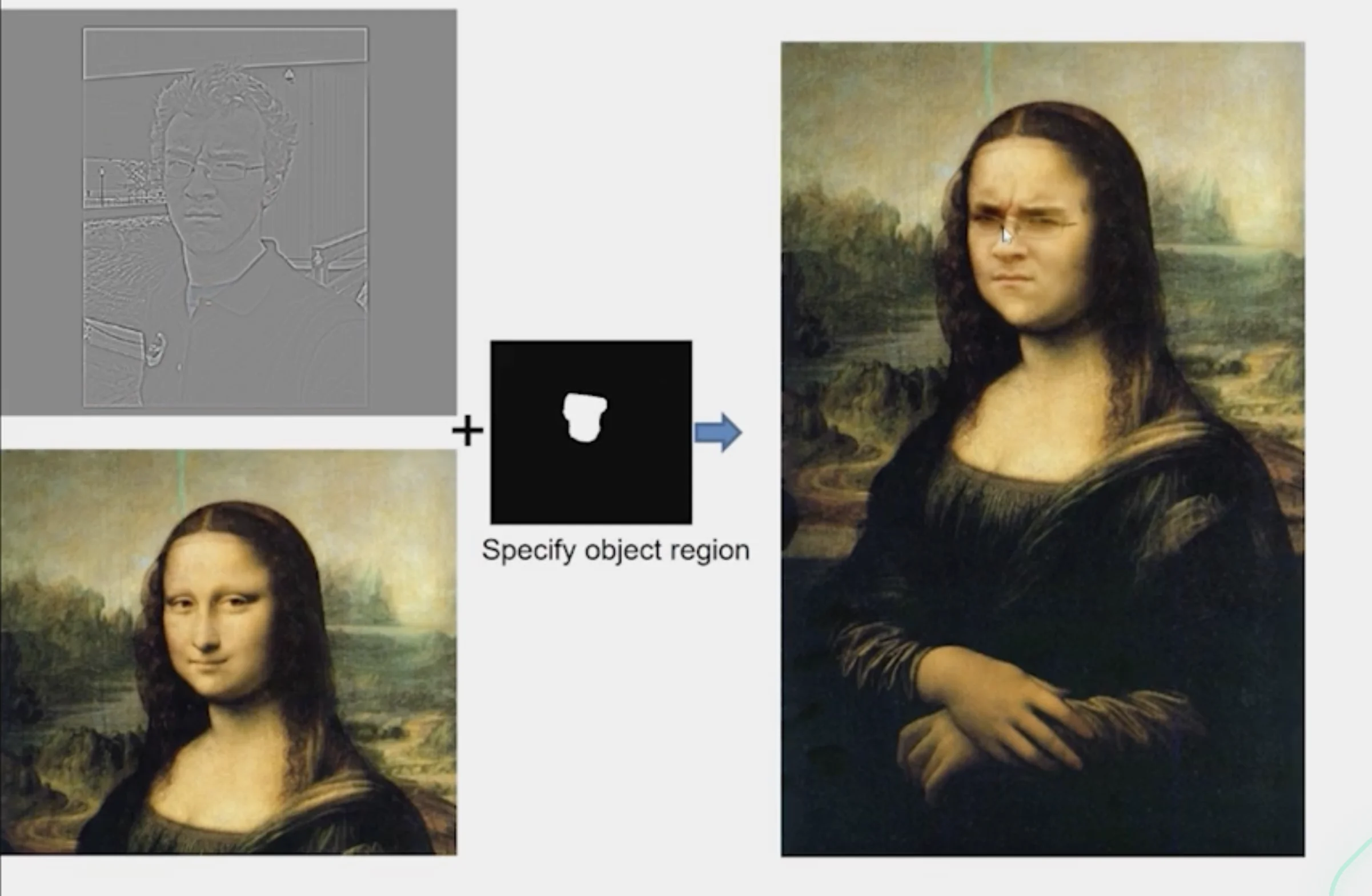
clipboard.png clipboard.png

Gradient-domain Editing

  • Instead of filtering the image, create a new image
  • measures the directional change in pixel intensity
  • Creation of Image
  • A least squares problem in terms of
  • Pixel intensities
  • Differences of pixel intensities

Line Equation and Parameters

yi=mxi+by_i = mx_i + b

Least Sqaures Objective

  • This is the least-squares fitting problem
m∗,b∗=arg min⁡m,b∑i(yi−(mxi+b))2m^*, b^* = \argmin_{m, b} \sum_i\left(y_i - (mx_i + b)\right)^2

Matrix Formulation

  • Given:
A=[x11x21⋮xn1],v=[mb],c=[y1y2⋮yn]A = \begin{bmatrix} x_1\quad 1 \\ x_2\quad 1 \\ \vdots \\ x_n\quad 1 \\ \end{bmatrix}, \quad v = \begin{bmatrix} m\\ b\\ \end{bmatrix}, \quad c = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}
  • We can write
{Av=cAv≈c(data is noisy)\begin{cases} Av = c \\ Av \approx c \quad \text{(data is noisy)} \end{cases}
  • With least squares form
v=arg min⁡v∣∣Av−c∣∣2v = \argmin_v \mid\mid Av - c \mid\mid^2
  • Try to derive v
∣∣Av−c∣∣2=(Av−c)⊺(Av−c)=v⊺A⊺Av−2c⊺Av+c⊺c\begin{align*} &\mid\mid Av - c \mid\mid^2 \\ &= (Av -c)^\intercal(Av -c) \\ &= v^\intercal A^\intercal Av - 2c^\intercal Av + c^\intercal c \\ \end{align*} ∇vE(v)=2A⊺(Av−c)=0  ⟹  A⊺Av=A⊺c  ⟹  v=(ATA)−1A⊺c\begin{align*} \nabla_v E(v) &= 2A^\intercal (Av - c) = 0 \\ &\implies A^\intercal Av = A^\intercal c \\ &\implies v = (A^TA)^{-1} A^\intercal c \end{align*}

Example

v=arg min⁡v∑i∈S,j∈Ni,∩S((vi−vj)−(si−sj))2+∑i∈,j∈,∩¬S((vi−tj)−(si−sj))2v = \argmin_v \sum_{i \in S, j \in N_i, \cap S} ((v_i - v_j) - (s_i - s_j))^2 + \sum_{i\in,j\in,\cap \neg S} ((v_i - t_j) - (s_i - s_j))^2

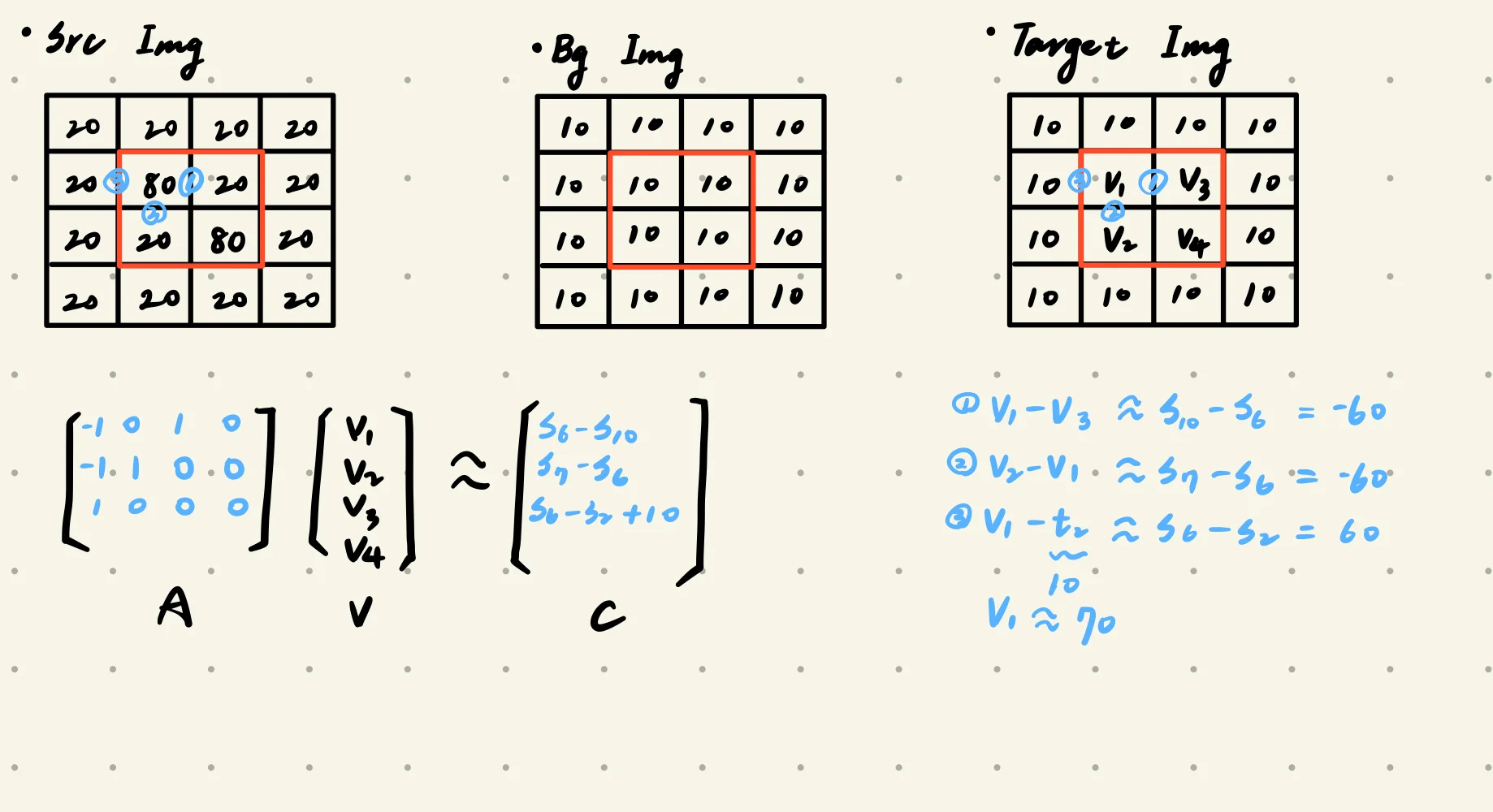
clipboard.png

  • source image:
  • the image containing the object to be pasted
  • background image:
  • the image to be pasted to
  • red:
  • regions to be used to insert patch from the source image

Constraints

∑i∈S,j∈Ni,∩S((vi−vj)−(si−sj))2\sum_{i \in S, j \in N_i, \cap S} ((v_i - v_j) - (s_i - s_j))^2
  • Inside the red region, the differences between neighboring pixels in the target should stay the same as in the source.
∑i∈,j∈,∩¬S((vi−tj)−(si−sj))2\sum_{i\in,j\in,\cap \neg S} ((v_i - t_j) - (s_i - s_j))^2
  • The difference between the pixels inside and outside the red regions should be the same in both the target image and the source image

Some Results

clipboard.png

Caution

What do we lose with Poisson Editing?

  • We lose the texture of the source image in the target image
  • Invariant to the overall color (only cares about the difference of color)

Blending with Mixed Gradients

  • Use foreground or background gradient with larger magnitude as the guiding gradient
v=arg min⁡v∑i∈S,j∈Ni∩S((vi−vj)−dij)2+∑i∈S,j∈Ni,∩¬S((vi−tj)−dij)2v = \argmin_v \sum_{i \in S, j \in N_i \cap S}((v_i - v_j) - d_{ij})^2 + \sum_{i \in S, j \in N_i, \cap \neg S} ((v_i - t_j) - d_{ij})^2

where

  • dijd_{ij} is the gradient from source or target with larger magnitude

clipboard.png

Things to Remember

1. Alpoha compositing

  • Need nice cut (intelligent scissor)
  • should feather

2. Laplacian pyramid blending

  • Smooth blending at low frequencies, sharp at high frequencies
  • usually used for stitching

3. Gradient domain editing

  • Also called Poisson Editing
  • Explicit control over what to preserve
  • Changes foreground color
  • Applicable for many things besides blending