5.2 Image Warping

clipboard.png

How would you make a sharpening filter using gradient domain processing? What are the constraints on the gradients and the intensities?

α(S(x,y)−S(x+1,y))≈t(x,y)−t(x+1,y)\alpha(S(x, y) - S(x + 1, y)) \approx t(x, y) - t(x + 1, y)

where

  • α>1\alpha > 1
  • We simply use α\alpha to increase the gradient to enlarge the difference between neighboring pixels

Image Warping

  • Changing the domain or corner of an image

clipboard.png

Parametric Warping

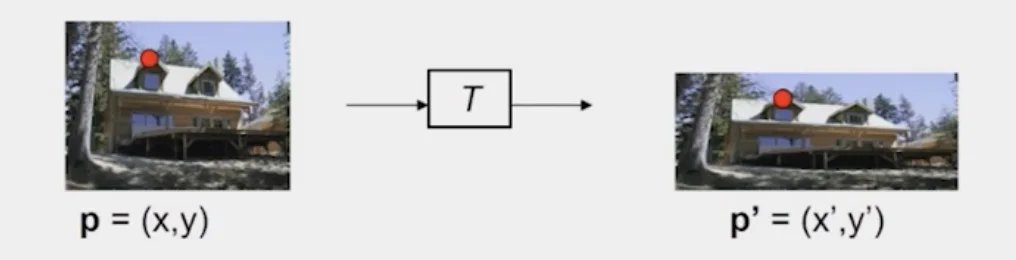
clipboard.png

  • Transformation TT is a coordinate-changing machine:
p′=T(p)p' = T(p)

What does it me3an that T is global?

  • Is the same for any point p
  • For lienar transformations, we can represent T as a matrix
p′=Mp[x′y′]=M[x′y′]\begin{align*} &p' = Mp \\ &\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \textbf{M} \begin{bmatrix} x' \\ y' \\ \end{bmatrix} \end{align*}

clipboard.png

Scaling

  • A coordinate means multiplying each of its components by a scalar

∙\bullet Uniform scaling

  • The scalar applied is the same for all components:

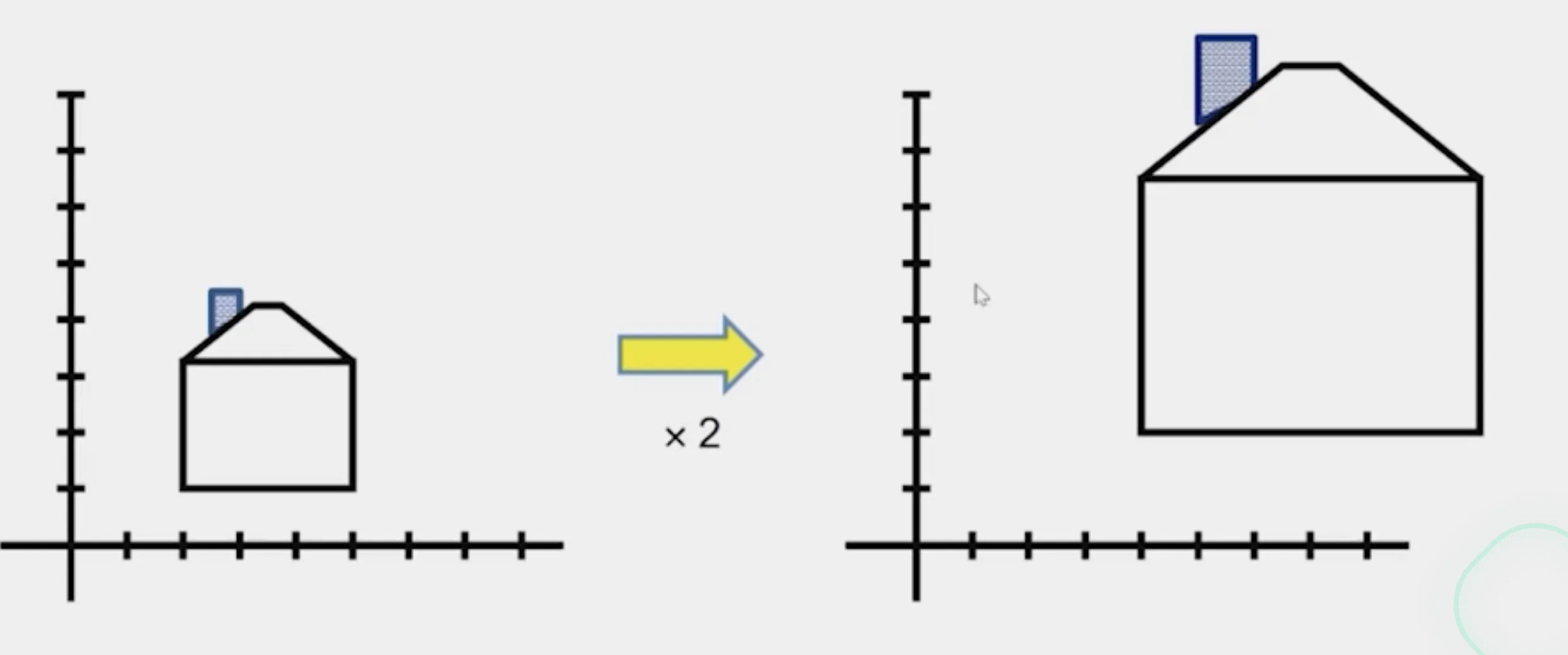
clipboard.png

∙\bullet Non-uniform scaling

  • different scalars per component:

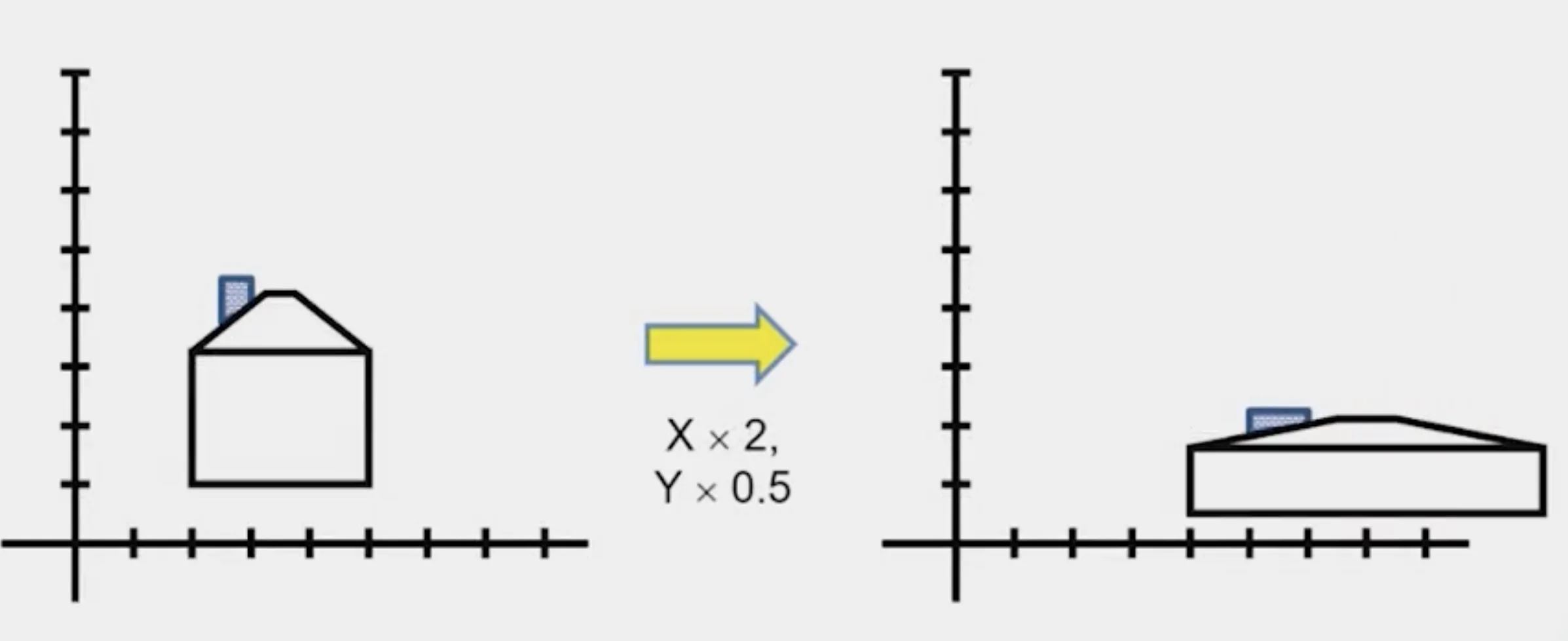
clipboard.png

Formula

x′=axy′=by[x′y′]=[a00b][xy]\begin{align*} &x' = ax \\ &y' = by \\ &\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = &\begin{bmatrix} a \quad 0 \\ 0 \quad b \\ \end{bmatrix} &\begin{bmatrix} x \\ y \\ \end{bmatrix} \end{align*}

Tip

To transform back from (x’, y’), you just change a and b to 1a\frac{1}{a} and 1b\frac{1}{b} (inverse of the matrix)

2-D Rotation

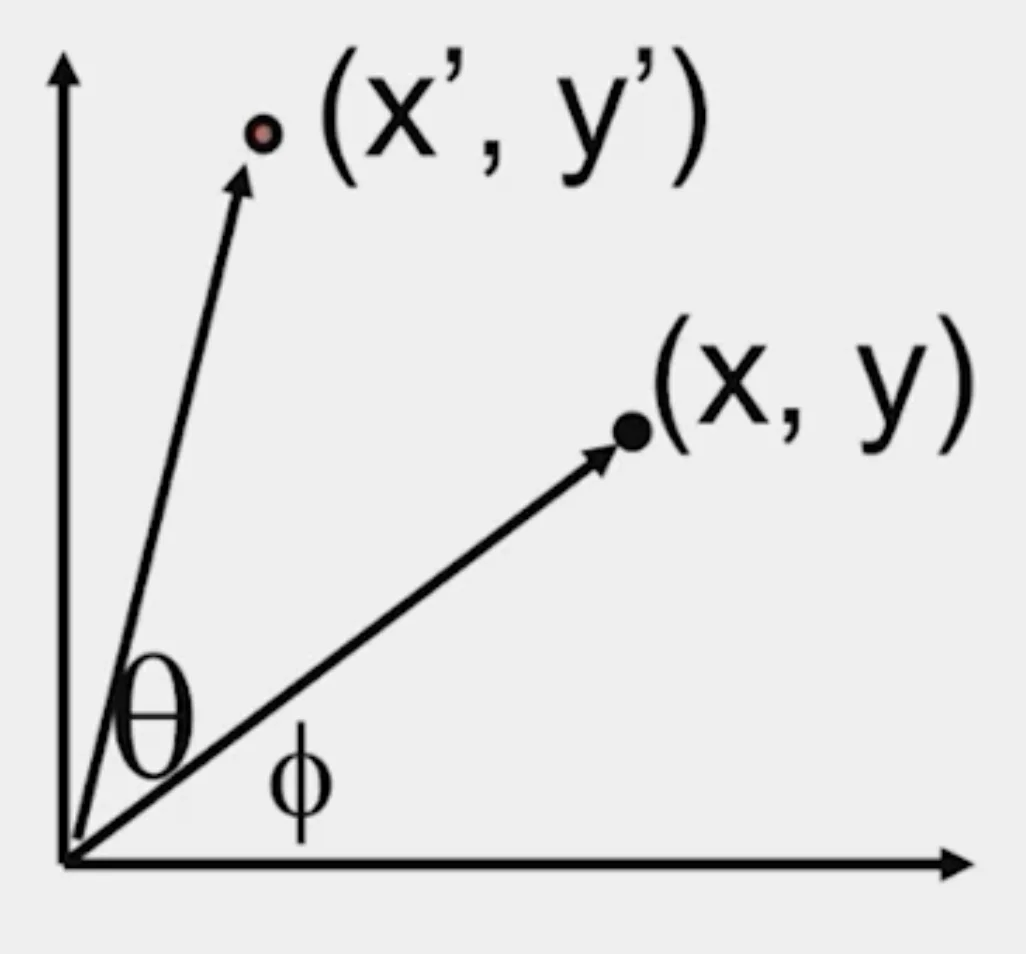
clipboard.png

x=rcos(ϕ)y=rsin(ϕ)x′=rcos(ϕ+θ)y′=rsin(ϕ+θ)\begin{align*} &x = rcos(\phi)\\ &y = rsin(\phi) \\ &x' = rcos(\phi + \theta) \\ &y' = rsin(\phi + \theta) \\ \end{align*} x′=r(cos(ϕ)cos(θ)−sin(ϕ)sin(θ))=xcos(θ)−y(sinθ)y′=r(sin(ϕ)cos(θ)+cos(ϕ)sin(θ))=xsin(θ)+ycos(θ)  ⟹  [x′y′]=[cos(θ)−sin(θ)sin(θ)cos(θ)][xy]\begin{align*} x' &= r(cos(\phi)cos(\theta) - sin(\phi)sin(\theta)) \\ &= xcos(\theta) - y(sin\theta)\\ y' &= r(sin(\phi)cos(\theta) + cos(\phi)sin(\theta)) \\ &= xsin(\theta) + ycos(\theta) \\ \implies &\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} &cos(\theta) \quad &-sin(\theta) \\ &sin(\theta) \quad &cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix} \end{align*}

Important

Even though coscos and sinsin are non-linear functions, x′x' and y′y' are linear combinations of xx and yy.

Tip

Inverse Transformation

  • Rotation by −θ-\theta
  • For rotation matrices R−1=RTR^{-1} = R^T

Operations for 2x2 Matrices

Identity

[x′y′]=[1001][xy]\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} 1 \quad 0 \\ 0 \quad 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix}

Scale around (0, 0)

[x′y′]=[sx00sy][xy]\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} s_x \quad 0 \\ 0 \quad s_y \\ \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix}

2D Rotate around (0, 0)

[x′y′]=[cos(θ)−sin(θ)sin(θ)cos(θ)][xy]\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} &cos(\theta) \quad &-sin(\theta) \\ &sin(\theta) \quad &cos(\theta) \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix}

2D Shear

  • Transform a rectangular shape to a parallegram
[x′y′]=[1kxky1][xy]\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} 1 \quad k_x \\ k_y \quad 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix}

Mirror about Y axis

[x′y′]=[−1001][xy]\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} -1 \quad 0 \\ 0 \quad 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix}

Mirror over (0, 0)

[x′y′]=[−100−1][xy]\begin{bmatrix} x' \\ y' \\ \end{bmatrix} = \begin{bmatrix} -1 \quad 0 \\ 0 \quad -1 \\ \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix}

Caution

2D translation is NOT FEASIBLE

Due to the consant terms for translating x and y

  • x′=x+txx' = x + t_x
  • y′=y+tyy' = y + t_y

Homogeneous Coordinates

  • Represent coordinates in 2 dimensions with a 3-vector
[xy]→⏞homogeneous coords[xy1]\begin{bmatrix} x \\ y \\ \end{bmatrix} \overbrace{\rightarrow}^{\text{homogeneous coords}} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix}
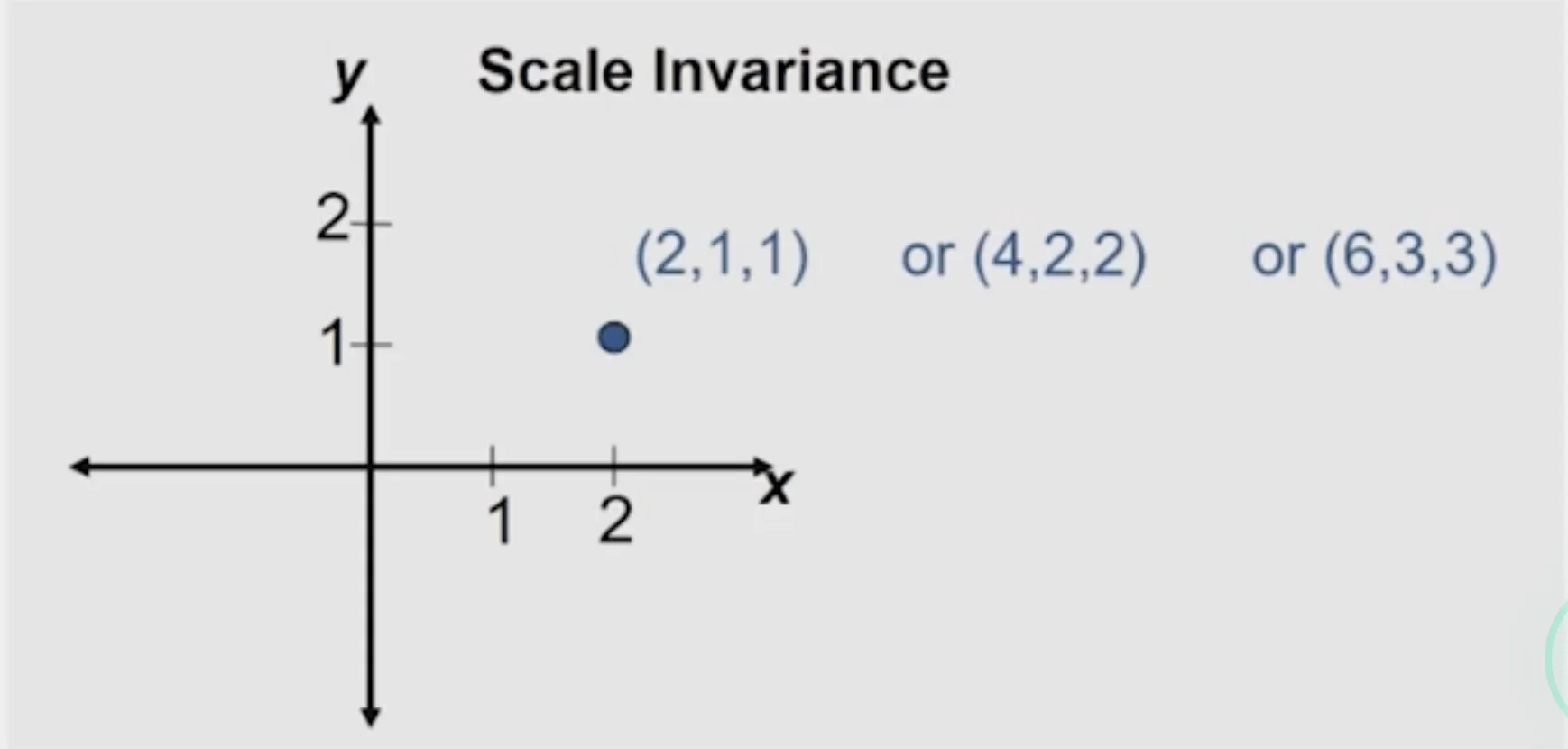
  • Homogeneous coordinates are scale-invariant
  • Any scale version of this vector represents the same point:
(X,Y,Z,1)∼(λX,λY,λZ,λ)(X, Y, Z, 1) \sim (\lambda X, \lambda Y, \lambda Z, \lambda)

clipboard.png

Warning

  • (x,y,0)(x, y, 0) represents a point at infinity
  • (0,0,0)(0, 0, 0) is not allowed

2D Image Transformations

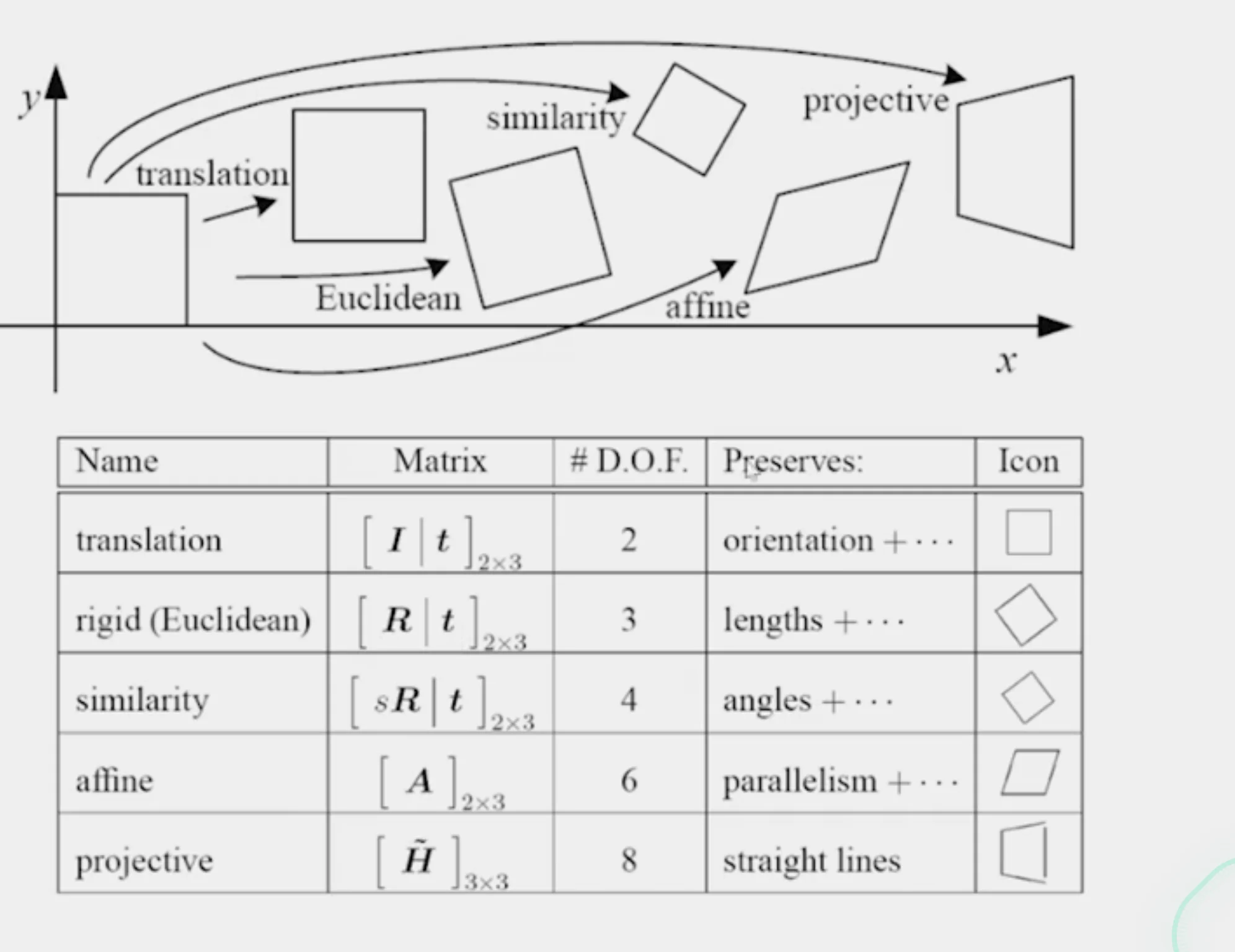
clipboard.png

∙\bullet Translation

Form

  • x′=x+tx,y′=y+tyx' = x + t_x, \quad y' = y + t_y

Matrix

[I∣t]\begin{bmatrix} I \mid t \end{bmatrix}

DoF

  • 2:(tx,ty)2: (t_x, t_y)

Preserves

  • Every relative geometry as it only shifts the pixels

∙\bullet Rigid (Euclidean)

  • Rotation + Translation

Form

  • x′=Rx+tx,y′=Ry+tyx' = Rx + t_x, \quad y' = Ry + t_y

Matrix

[R∣t],R=[cos(θ)−sin(θ)sin(θ)cos(θ)]\begin{bmatrix} R \mid t \end{bmatrix}, \quad R= \begin{bmatrix} &cos(\theta) \quad &-sin(\theta) \\ &sin(\theta) \quad &cos(\theta) \\ \end{bmatrix}

DoF

  • 3:θ,(tx,ty)3: \theta, (t_x, t_y)

Preserves

  • Lengths, angles, parallelism, straight lines, orientation.

∙\bullet Similarity

  • uniform scale + rotation + translation

Form

  • x′=sRx+tx,y′=sRy+ty(s>0)x' = sRx + t_x, \quad y' = sRy + t_y \quad(s > 0)

Matrix

[sR∣t],R=[cos(θ)−sin(θ)sin(θ)cos(θ)]\begin{bmatrix} sR \mid t \end{bmatrix}, \quad R= \begin{bmatrix} &cos(\theta) \quad &-sin(\theta) \\ &sin(\theta) \quad &cos(\theta) \\ \end{bmatrix}

DoF

  • 4:s,θ,(tx,ty)4: s, \theta, (t_x, t_y)

Preserves

  • Angles and shape

∙\bullet Affine

  • linear 2x2 translation

Form

  • x′=Ax+tx,y′=Ay+ty(A is any 2x2 matrix)x' = Ax + t_x, \quad y' = Ay + t_y \quad(\text{A is any 2x2 matrix})

Matrix

[A∣t]\begin{bmatrix} A \mid t \end{bmatrix}

DoF

  • 6:A=[abcd],(tx,ty)6: A = \begin{bmatrix}a\quad b \\ c\quad d\end{bmatrix}, (t_x, t_y)

Preserves

  • Parallelism and ratios of lengths along a line.

∙\bullet Projective (Homography)

  • Full 3×33 \times 3

Form

  • x~′∼Hx~(H∈R3×3,x~=(x,y,1)T)\tilde{x}' \sim H\tilde{x} \quad \quad(H \in \R^{3 \times 3}, \tilde{x} = (x, y, 1)^T)

Matrix

H=[abcdefghi]H = \begin{bmatrix} a \quad b \quad c \\ d \quad e \quad f \\ g \quad h \quad i \\ \end{bmatrix}

DoF

  • 8:A=98: A = 9 entries minus 1 overall scale constraint

Preserves

  • Straight lines. Parallel lines need not remain parallel.