6.1 Image Morphing

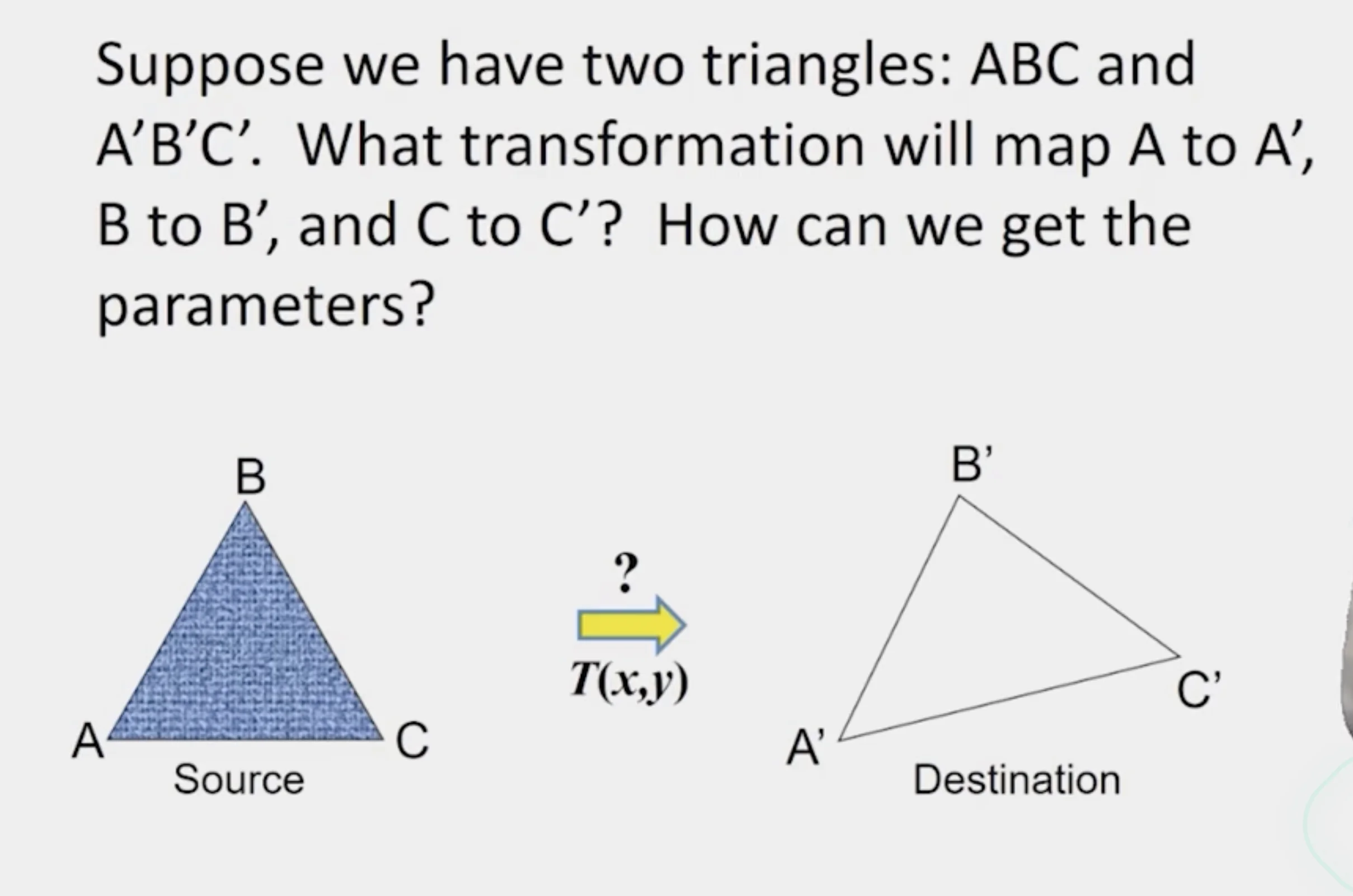
clipboard.png

  • Affine transformation

Image Morphing

  • How do we map intensities from one image to another image

Forward Mapping

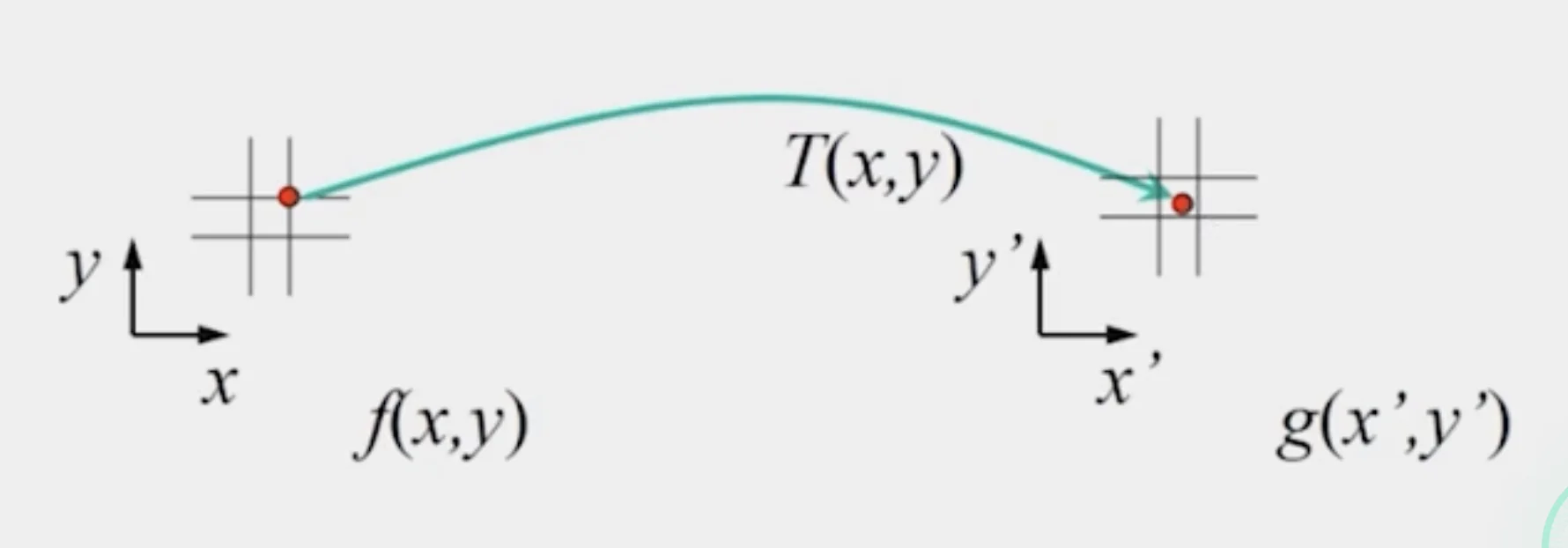
clipboard.png

  • Send each pixel f(x,y)f(x, y) to its corresponding location (x′,y′)=T(x,y)(x', y') = T(x, y) in the second image
  • Use splatting if the pixel to be transferred lies in between two pixels in the target image
  • Distribute color among neighboring pixels (x′,y′)(x', y')
  • The neighboring pixels are partly colored with the current pixel

Caution

  • You may create a lot of artifacts when the number of pixels is small
  • You may have a lot of blank pixels when the number of pixels is large

Inverse Mapping

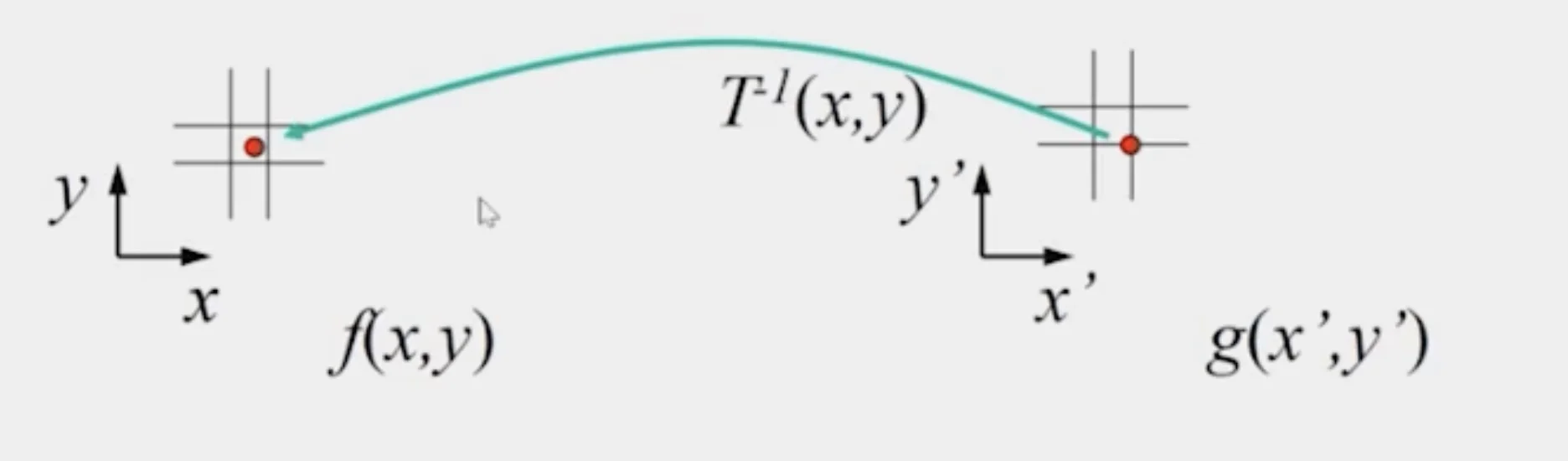
clipboard.png

  • Find the position in the source image from the target image
  • Get each pixel g(x′,y′)g(x', y') from its corresponding location (x,y)=T−1(x′,y′)(x, y) = T^{-1}(x', y') in the first image
  • Use interpolation if the pixel to be transferred lies in between two pixels in the source image
  • nearest neighbor
  • bilinear
  • Gaussian
  • bicubic

Bilinear Interpolation

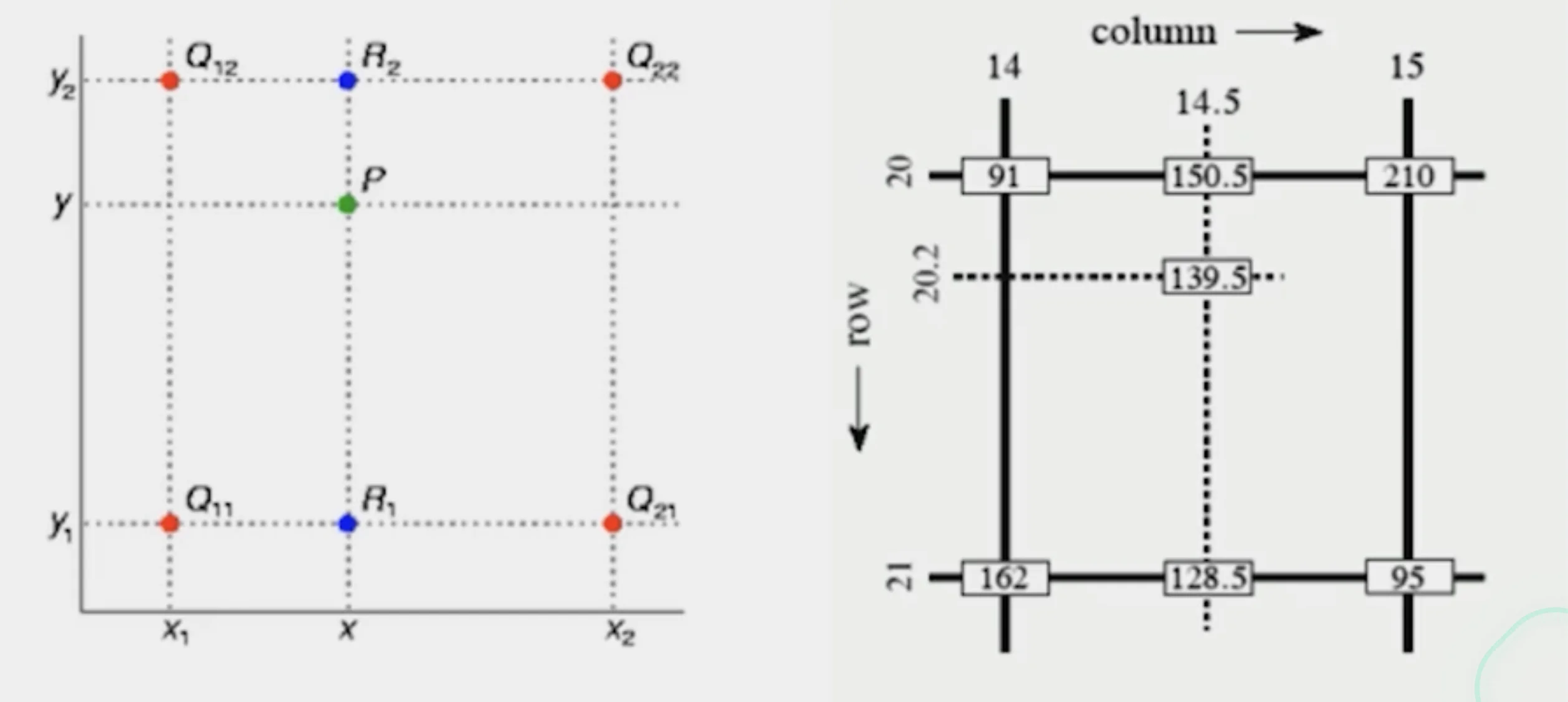
clipboard.png

  • estimates the pixel value at a non-integer position (x,y)(x, y) using the four nearest pixels surrounding it.
f(x,y)≈[1−xx][f(0,0)f(0,1)f(1,0)f(1,1)][1−yy]f(x, y) \approx \left[1 - x \quad x \right] \begin{bmatrix} f(0,0) \quad f(0, 1) \\ f(1, 0) \quad f(1, 1)\end{bmatrix} \begin{bmatrix}1 - y \\ y\end{bmatrix}
  1. Interpolate along x between each pair of horizontal
  2. Then interpolate those results along y.

Tip

Usually, inverse mapping eliminates holes; however, it requires invertible warp function

Morphing = Object Averaging

clipboard.png

  • The aim is to find “an average” between two objects
  • NOT an average of two images of objects
  • an image of average object
  • involves transforming both the coordinates (alignment) and the intensities (texture combination)
  • Smooth transition →\rightarrow weighted average over time

Averaging Points

  • What’s the average of P and Q?

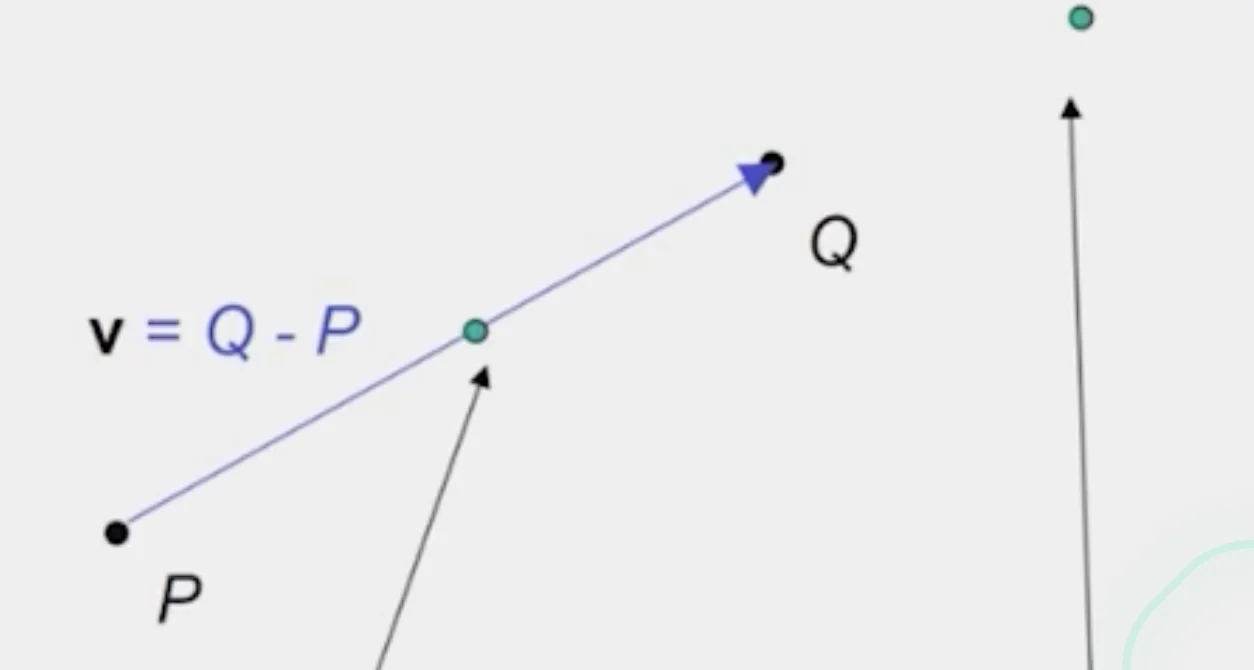
clipboard.png

Linear Interpolation

  • Given 0<t<10 < t < 1
  • New point: P+t(Q−P)P + t(Q - P)
  • Or: (1−t)P+tQ(1 - t)P + tQ
  • Meaning
  • Generate intermediate frames between the source and target
  • Effect
  • Smoothly blends position and color between two images

Extrapolation

  • Given t>1,t<0 t > 1, t < 0
  • New point: P+t(Q−P)P + t(Q - P)
  • Or: (1−t)P+tQ(1 - t)P + tQ
  • Meaning
  • Moving beyond the original range of blending
  • Effect
  • t<0t < 0: extrapolates before the source
  • t>1t > 1: extrapolate past the target
  • Produces exaggerated transformation

Cross-Dissolve

clipboard.png

  • Interpolate whole images:
Imagehalfway=(1−t)×Image1+t×Image2Image_{halfway} = (1 - t) \times Image_1 + t \times Image_2
  • This is called cross-dissolve in film industry
  • As long as the change of color values is monotonous, interpolation would work

Important

If the images are not aligned, you need to align them first and then cross-dissolve

Local warp, then cross-dissolve

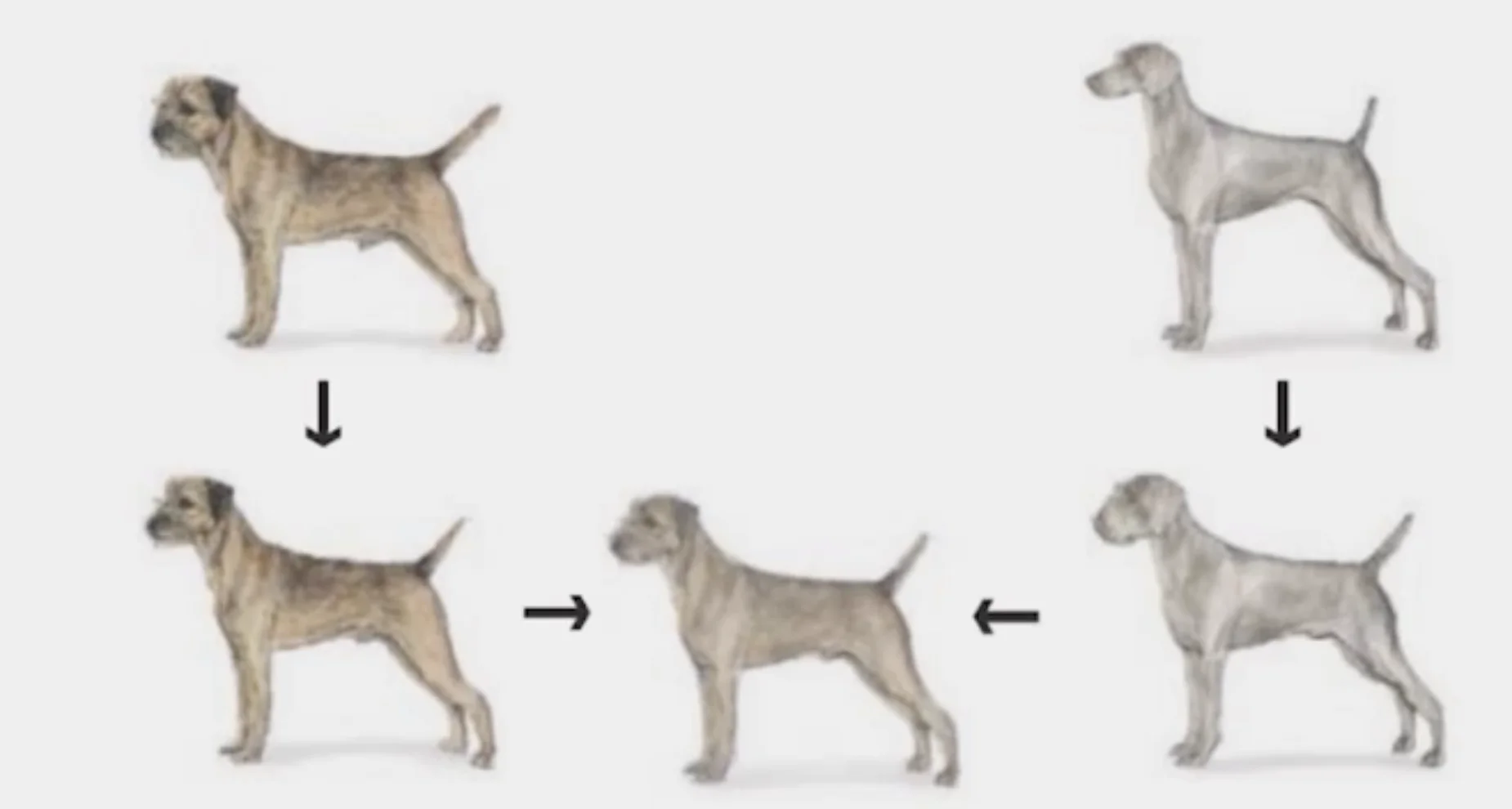
clipboard.png

Feature matching

  • Nose to nose, tail to tail, etc.
  • This is a local (non-parametric) warp

Morphing Procedure

  1. Find the average shape
  • local warping
  1. Find the average color
  • Cross-dissolve the warped images

Warp Specification - dense

clipboard.png

1. Specify corresponding points

clipboard.png

2. Triangular Mesh

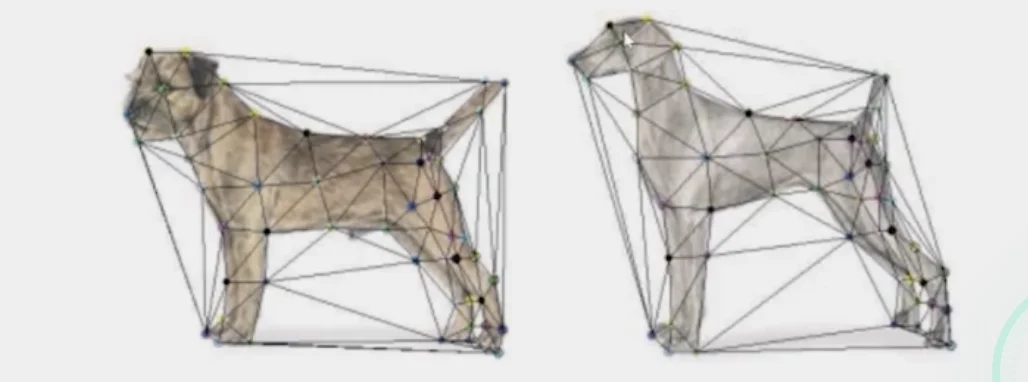
clipboard.png

  • Define a triangular mesh over the points
  • same mesh in both images
  • Now we have triangle to triangle correspondences
  • Warp each triangle separately from source to target
  • Affine warp with three corresponding points

Triangulations

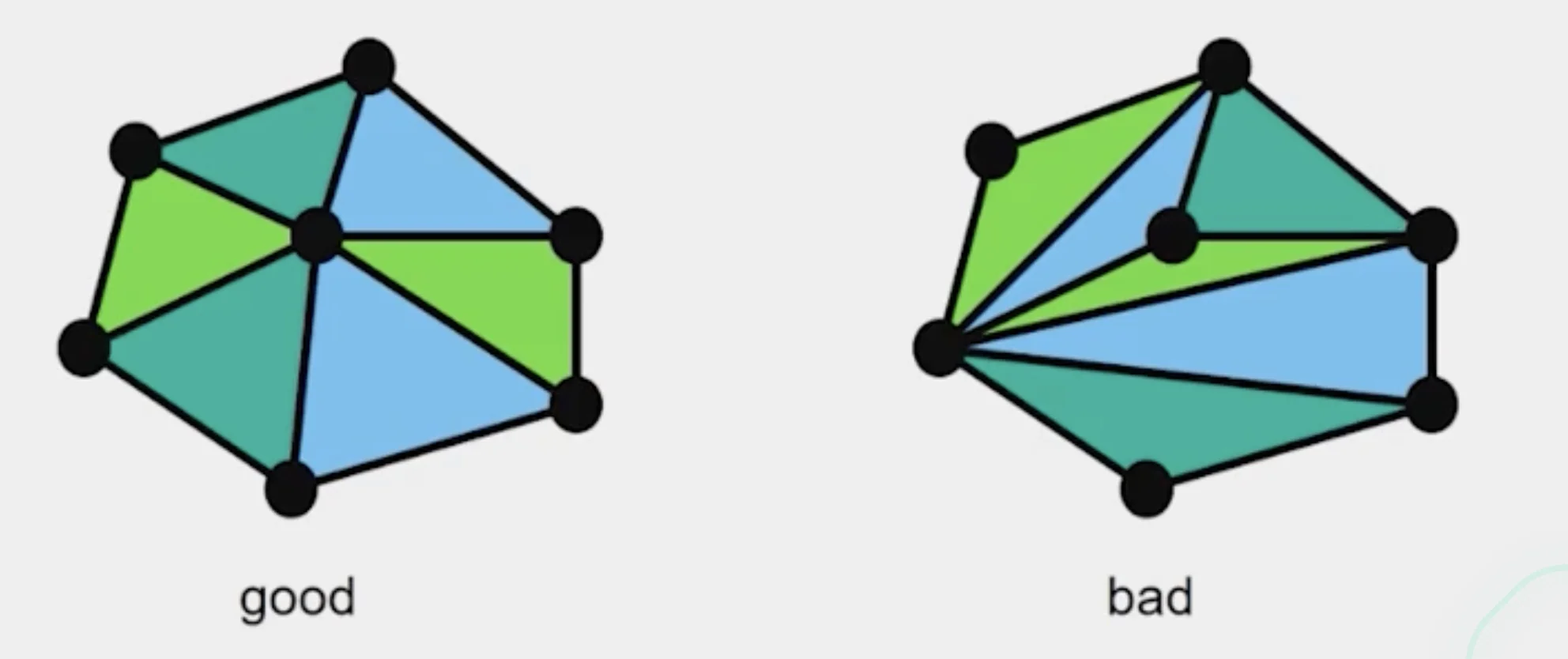
clipboard.png

  • A partition of the convex hull to triangles whose vertices are the points, and do not contain other points
  • O(n3)O(n^3) Algorithm
Repeat until impossible
1. Select two sites
2. If the dedge connecting them does not intersect previous edges, keep it.
  • Quality
  • A triangulation T1T_1 is better than T2T_2 if the smallest angle of T1T_1 is larger than the smallest angle of T2T_2

Delaunay Triangulation by Duality

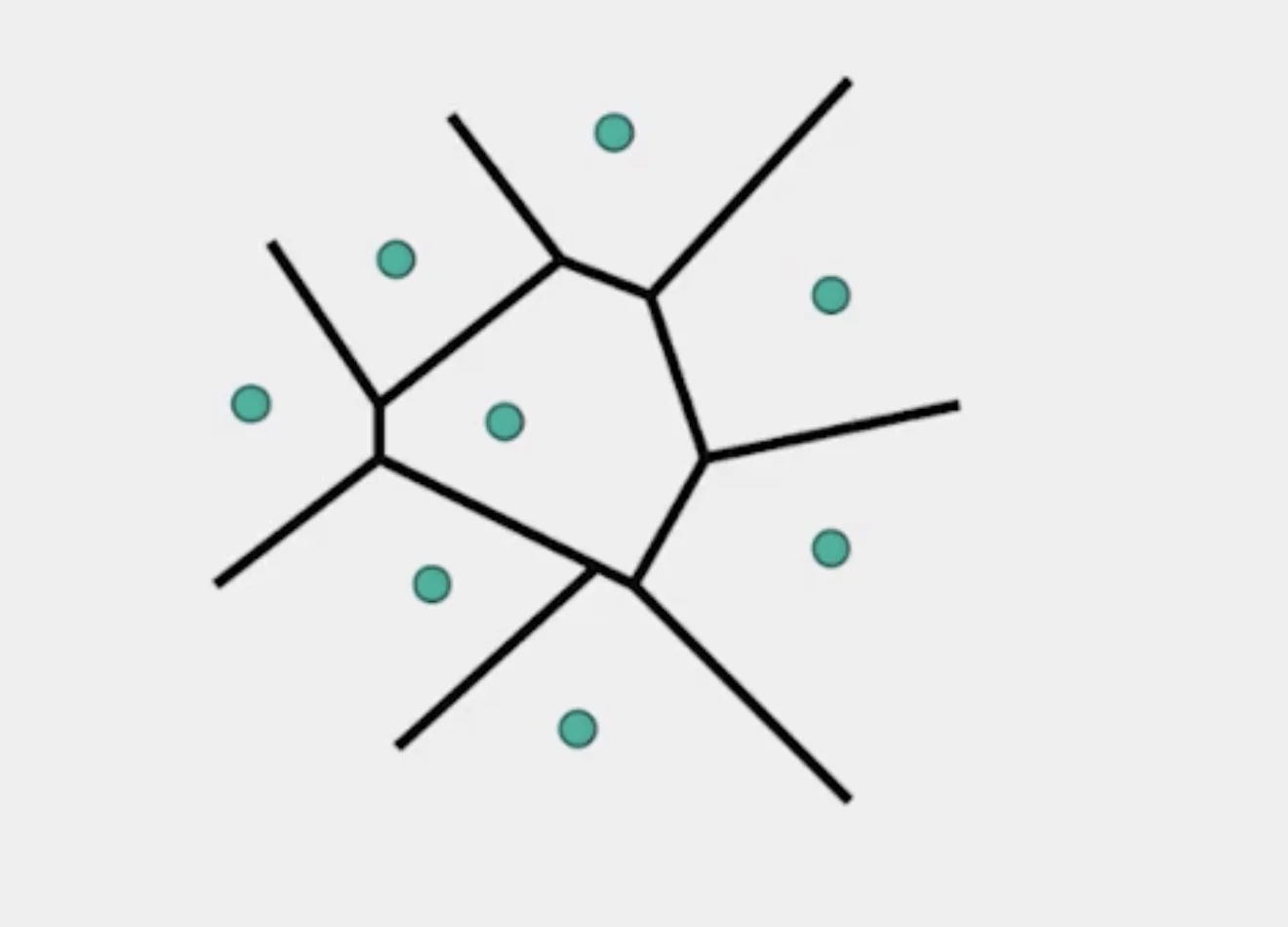
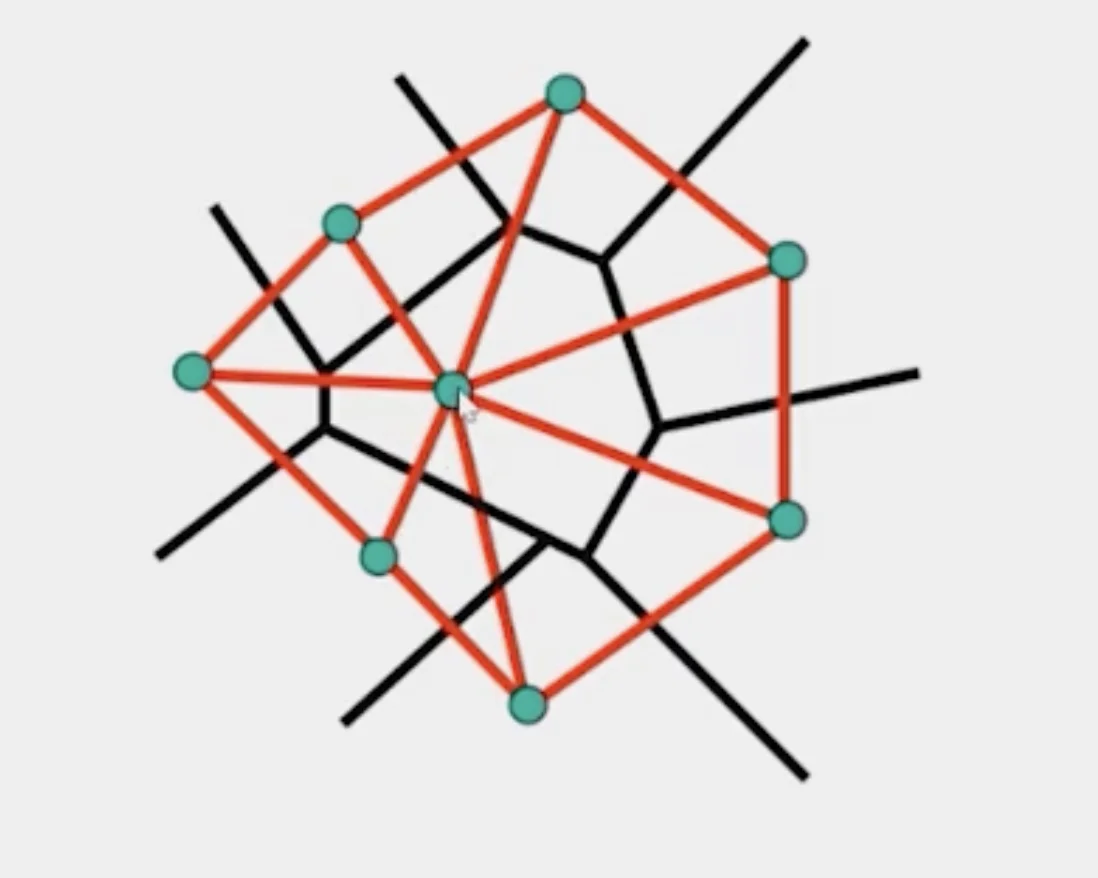
clipboard.png clipboard.png

  • Draw the dual to the Voronoi diagram by connecting each two neighboring sites in the Voronoi diagram.
  • The DT may be constructed in O(nlogn) time

3. Morphing Sequence

3-1. Create an intermediate shape (by interpolation)

  • How do we create an intermediate shape at time tt?
  • Assume t=[0,1]t = [0, 1]
  • (1−t)×p1+t×p0(1 - t) \times p_1 + t \times p_0

3-2. Warp both images towards it

3-3. Cross-dissolve the colors in the newly warped images

Summary of Morphing

  1. Define corresponding points
  2. Define triangulation on points
  • Use same triangulation for both images
  1. For each t = 0:step:1
  2. Compute the average shape (weighted average of points)
  3. For each pixel in the triangle, find the corresponding points in each image and set value to the weighted average (warp image toward the average shape)
  4. Save the image as the next frame of the sequence