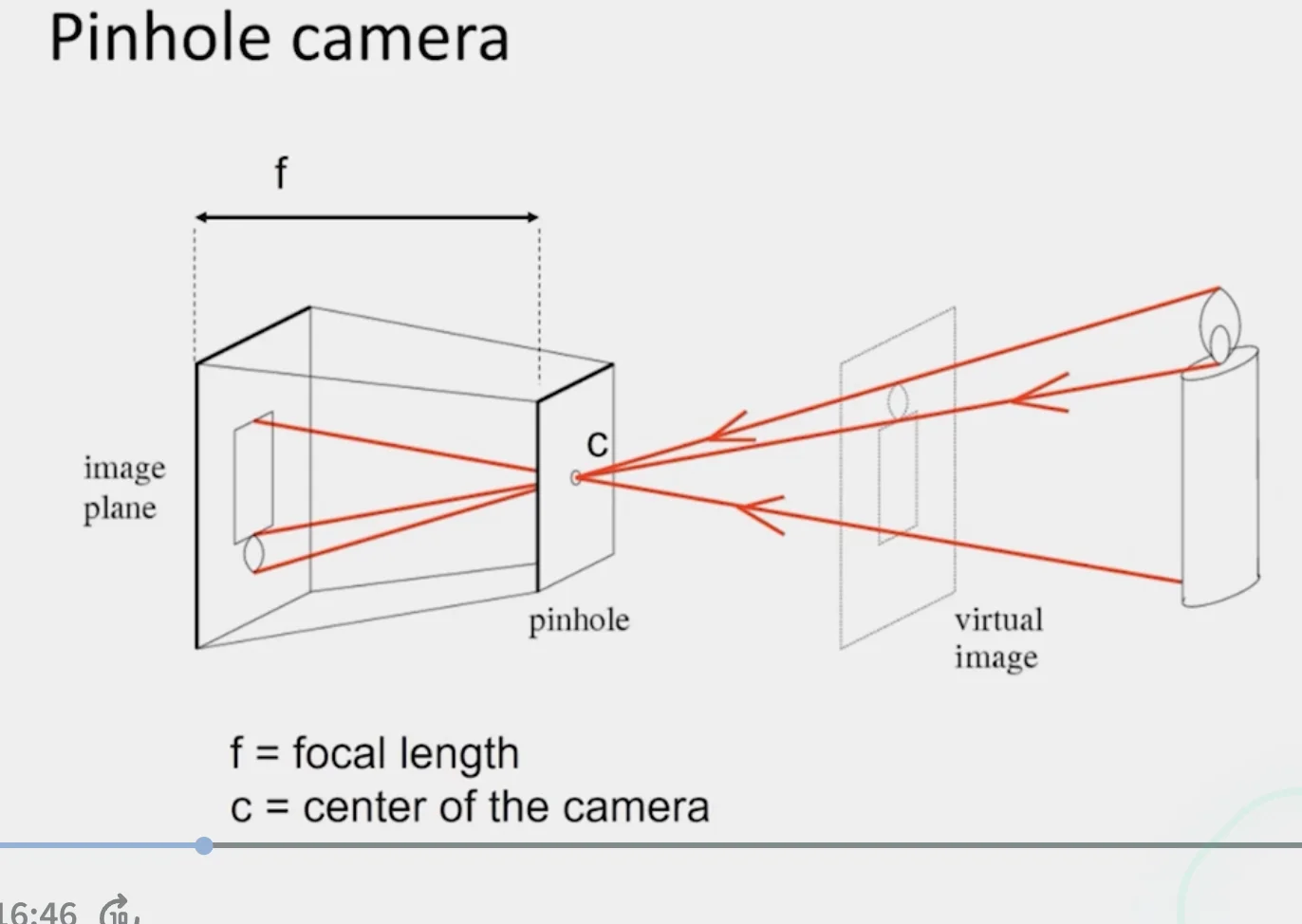
6.2 Pinhole Camera

Projective Geometry

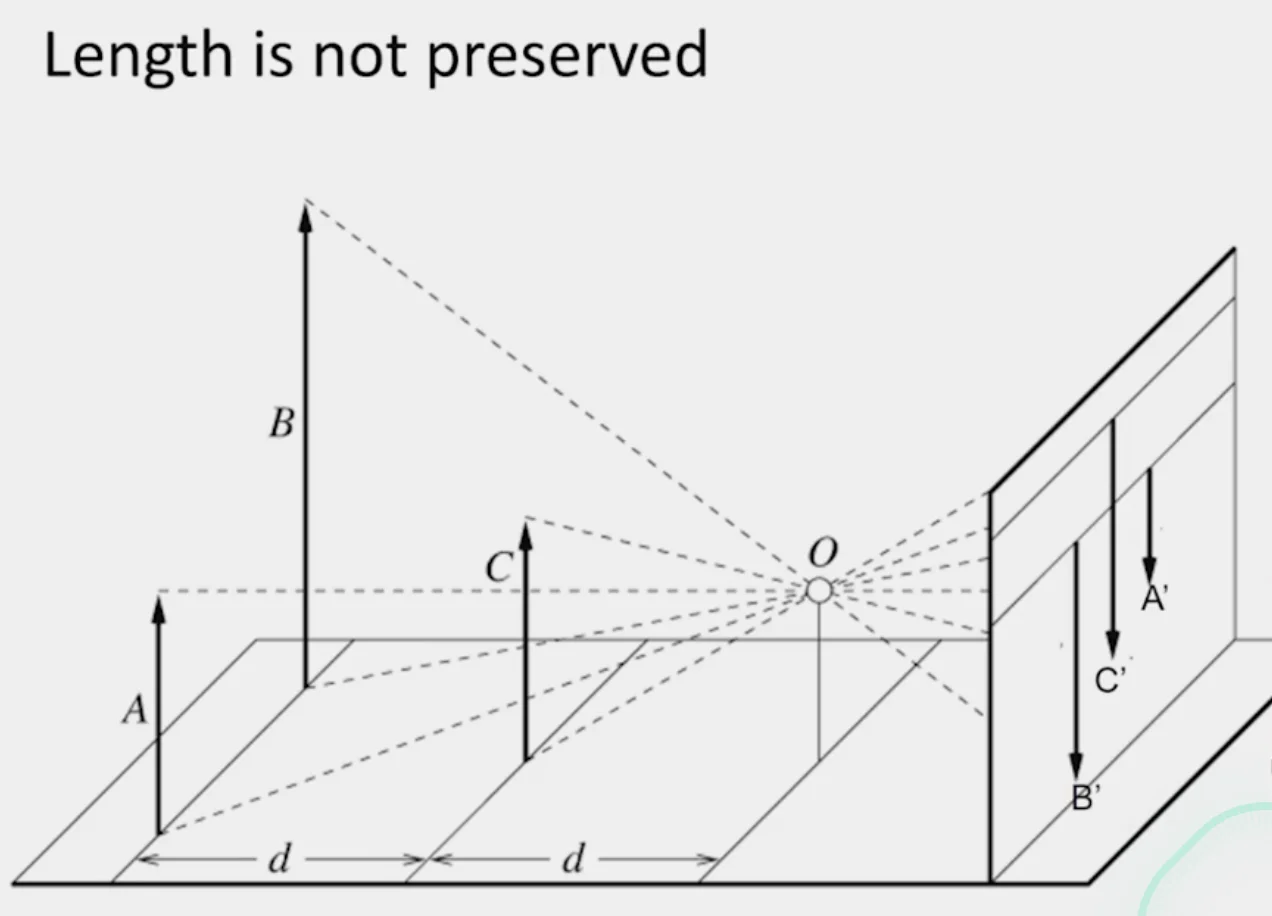
  • Angless and length are lost

clipboard.png clipboard.png

Vanishing Points and Lines

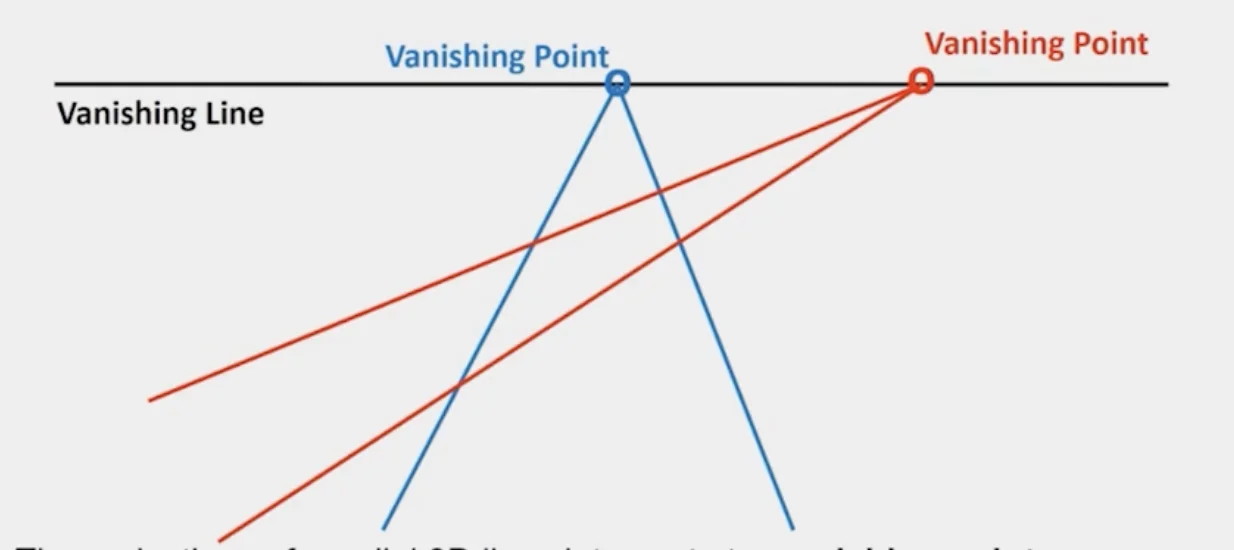
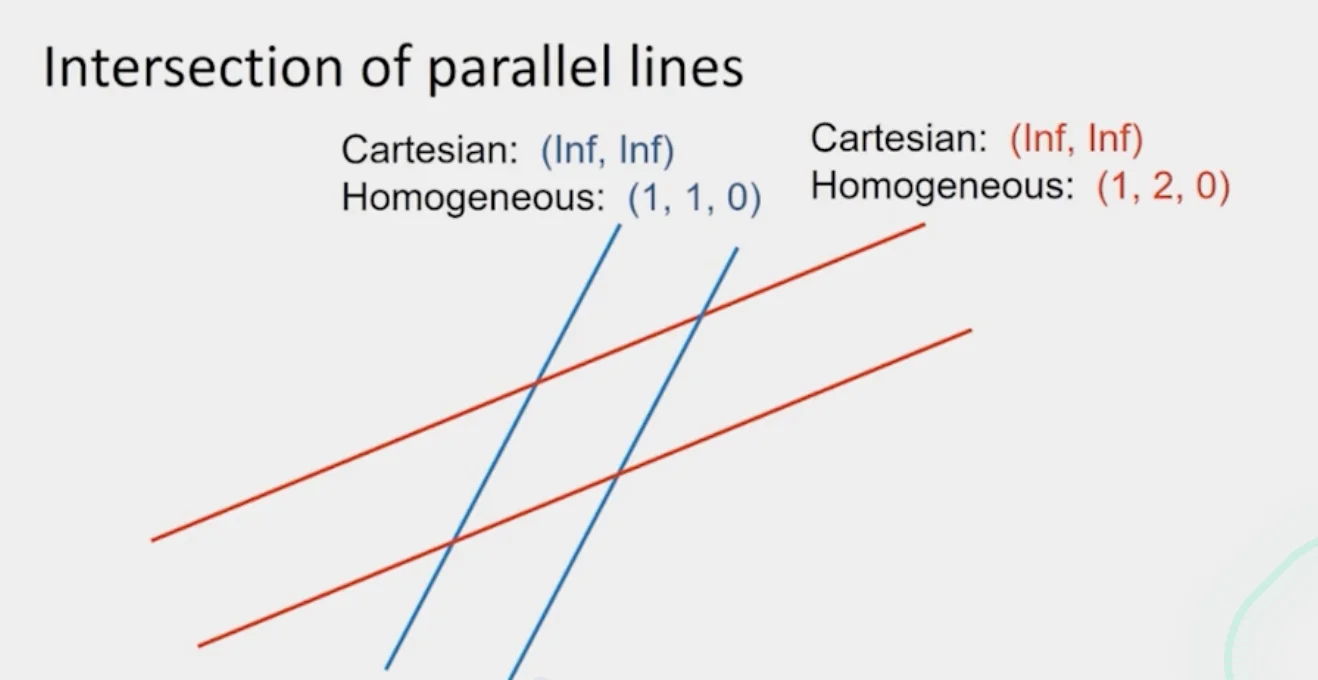
clipboard.png

  • The projections of parallel 3D lines intersect at a vanishing point
  • vanishing point →\rightarrow 3D direction of a line
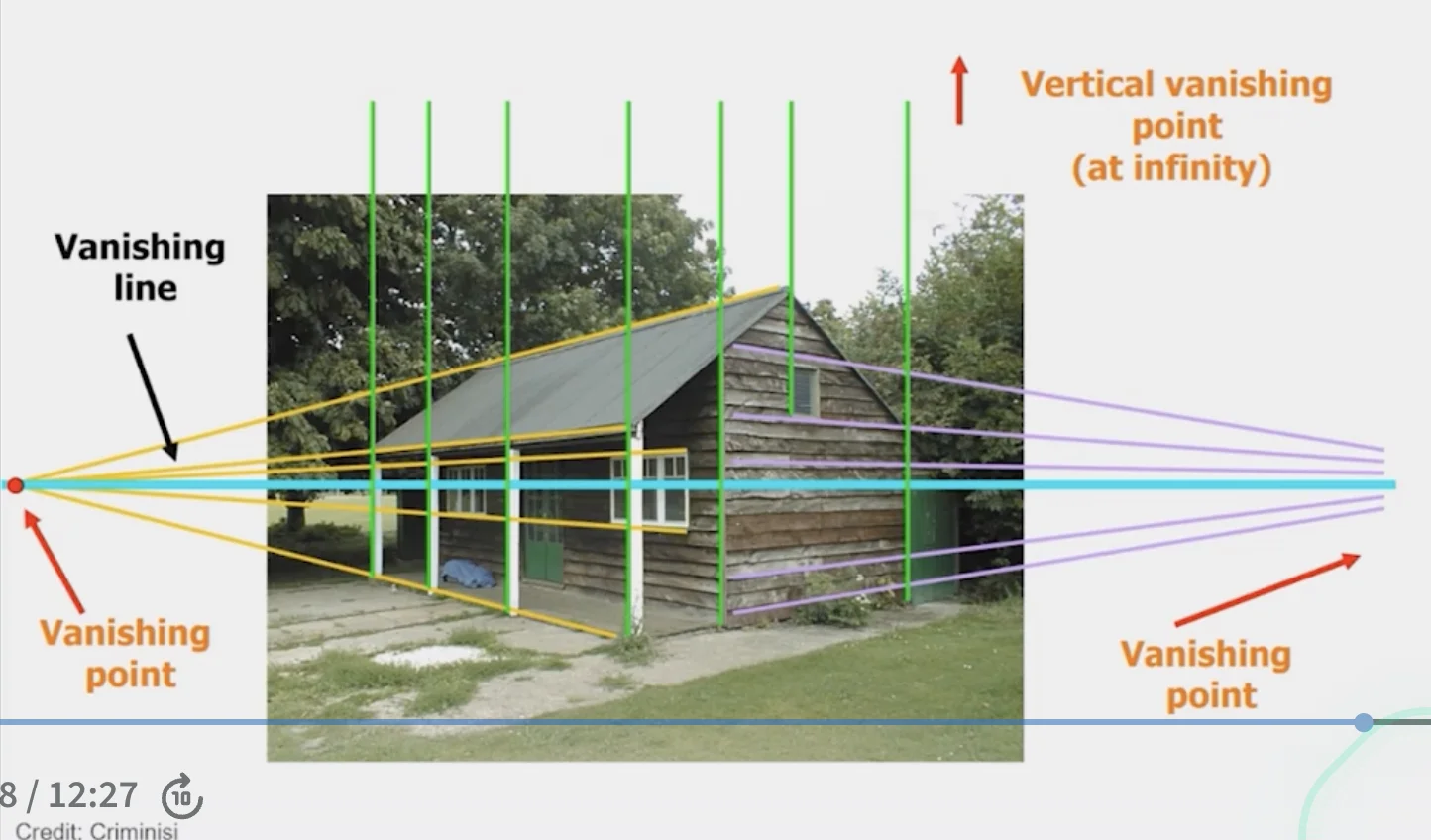
  • The projections of parallel 3D lines intersect at a vanishing line
  • vanishing line →\rightarrow 3D orientation of a surface
  • If a set of parallel 3D lines are also parallel to a particular plane, their vanishing point will lie on the vanishing line of the plane

clipboard.png

Projection: world coordinates →\rightarrow image coordinates

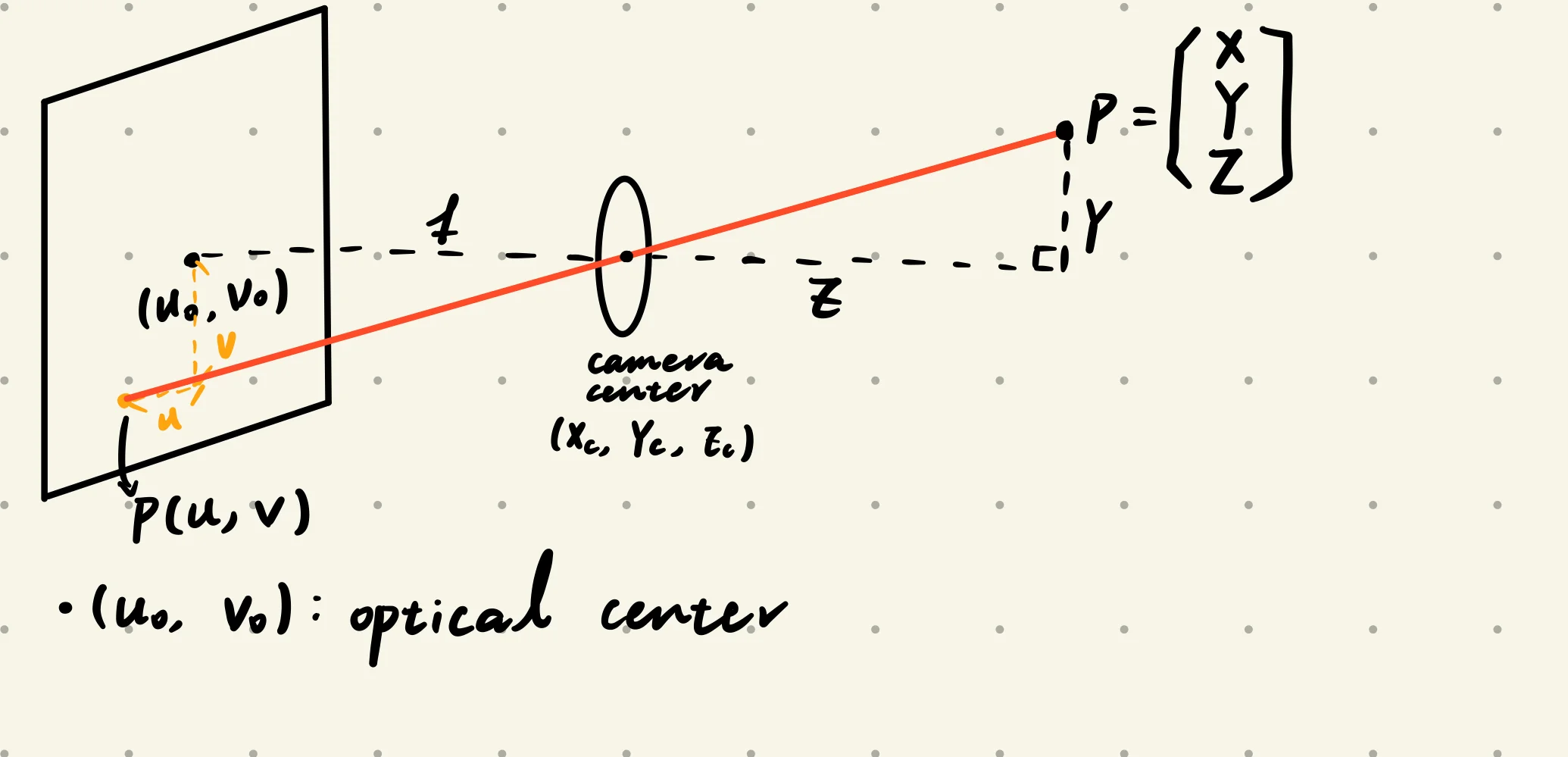
clipboard.png

Y−YcZ=v−v0fv=fY−YcZ+v0u=fX−XcZ+u0\frac{Y - Y_c}{Z} = \frac{v - v_0}{f} \\ v = f\frac{Y - Y_c}{Z} + v_0 \\ u = f\frac{X - X_c}{Z} + u_0

clipboard.png

Projection Matrix

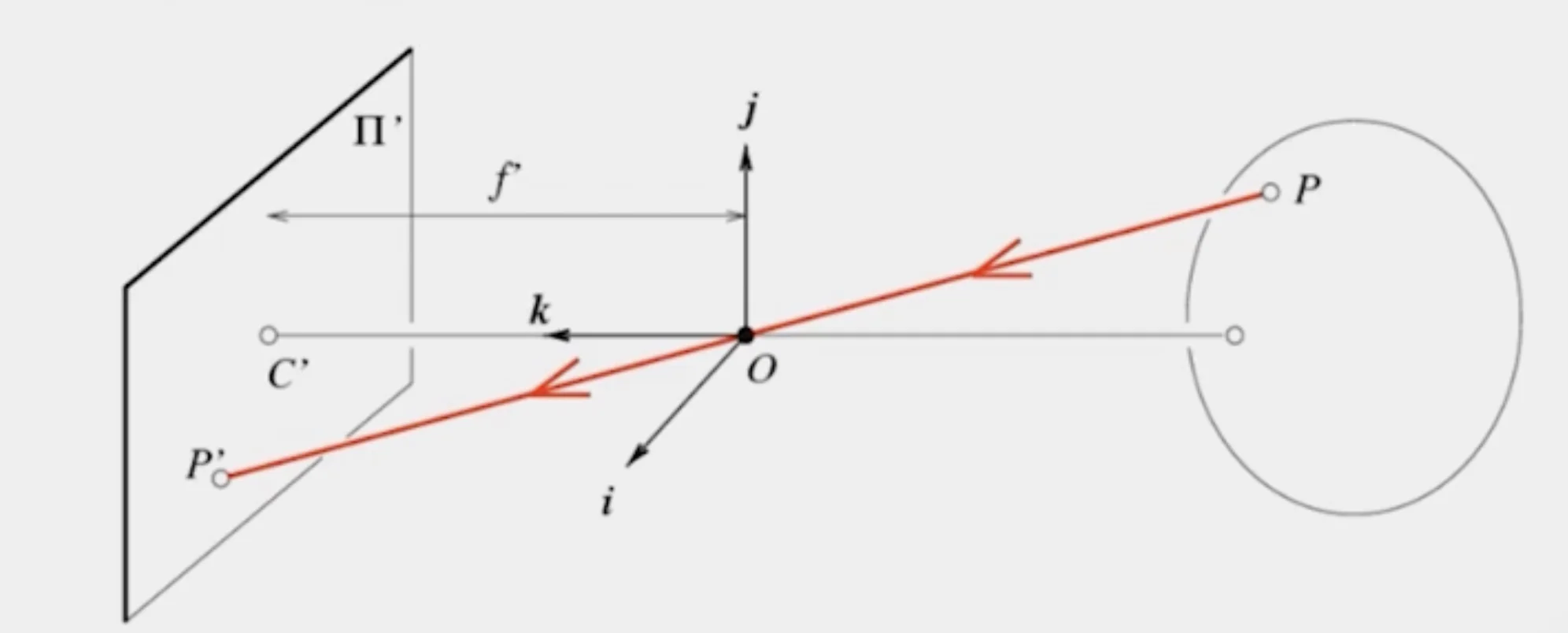
clipboard.png

{wu=fxwv=fy(w=z)  ⟹  {u=fxzv=fyz\begin{cases} wu = fx \\ wv = fy \\ \end{cases} \quad (w = z) \\ \implies \begin{cases} u = \frac{fx}{z} \\ v = \frac{fy}{z} \\ \end{cases}
  • Intrinsic Assumptions
  • Unit aspect ratio
  • Principal point at (0, 0)
  • No skew
  • Extrinsic Assumptions
  • No rotation
  • Camera at (0, 0, 0)
x=K[I0]X  ⟹  w[uv1]=[f0000f000010][xyz1]x = K[I \quad 0] X \implies w\begin{bmatrix}u \\ v \\ 1\end{bmatrix} = \begin{bmatrix} f &0 &0 &0 \\ 0 &f &0 &0 \\ 0 &0 &1 &0 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix}

where

K=[f000f0001]K = \begin{bmatrix} f &0 &0 \\ 0 &f &0 \\ 0 &0 &1 \\ \end{bmatrix}

If not at (0, 0)

K=[f0u00fv0001](u=fxz+u0)K = \begin{bmatrix} f &0 &u_0 \\ 0 &f &v_0 \\ 0 &0 &1 \\ \end{bmatrix} \quad (u = \frac{fx}{z} + u_0)

If pixels are not square

K=[α0u00βv0001]({α:scale of focal in x directionβ:scale of focal in y direction)K = \begin{bmatrix} \alpha &0 &u_0 \\ 0 &\beta &v_0 \\ 0 &0 &1 \\ \end{bmatrix} \quad \left( \begin{cases} \alpha: \text{scale of focal in x direction} \\ \beta: \text{scale of focal in y direction} \end{cases} \right)

If pixels are skewed

K=[αsu00βv0001]K = \begin{bmatrix} \alpha &s &u_0 \\ 0 &\beta &v_0 \\ 0 &0 &1 \\ \end{bmatrix}

Allow Camera Translation

x=K[I∣t]X  ⟹  w[uv1]=[α0u00βv0001][100tx010ty001tz][xyz1]\begin{align*} &x = K[I \mid t]X \\ &\implies w \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha &0 &u_0 \\ 0 &\beta &v_0 \\ 0 &0 &1 \\ \end{bmatrix} \begin{bmatrix} 1\quad 0\quad 0\quad t_x \\ 0\quad 1\quad 0\quad t_y \\ 0\quad 0\quad 1\quad t_z \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \end{align*}

Warning

[xyz1]\begin{bmatrix} x \\ y\\ z\\ 1 \end{bmatrix} is not the camera center. It is the amount of 3D points that have to have to move in order to enter the camera’s coordinates

Allow camera rotation

x=K[R∣t]X  ⟹  w[uv1]=[αsu00βv0001][r11r12r13txr21r22r23tyr31r32r33tz][xyz1]\begin{align*} &x = K[R \mid t]X \\ &\implies w \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} \alpha &s &u_0 \\ 0 &\beta &v_0 \\ 0 &0 &1 \\ \end{bmatrix} \begin{bmatrix} r_{11}\quad r_{12}\quad r_{13}\quad t_x \\ r_{21}\quad r_{22}\quad r_{23}\quad t_y \\ r_{31}\quad r_{32}\quad r_{33}\quad t_z \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} \end{align*}

Important

  • Matrix R is orthonormal
  • DoF
  • Intrinsic matrix: 5
  • Extrinsic matrix: 6

Vanishing Point = Projection from infinity

p=K[Rt][xyz0]=KR[xyz]=K[xRyRzR]\begin{align*} p &= K [R \quad \cancel{t}] \begin{bmatrix} x \\ y \\ z \\ \cancel{0} \\ \end{bmatrix} \\ &= KR \begin{bmatrix} x \\ y \\ z \end{bmatrix} \\ &= K \begin{bmatrix} x_R \\ y_R \\ z_R \\ \end{bmatrix} \end{align*} w[uv1]=[f0u00fv0001][xRyRzR]  ⟹  {u=fxRzR+u0v=fyRzR+v0w \begin{bmatrix} u \\ v \\ 1 \end{bmatrix} = \begin{bmatrix} f \quad 0 \quad u_0 \\ 0 \quad f \quad v_0 \\ 0 \quad 0 \quad 1 \end{bmatrix} \begin{bmatrix} x_R \\ y_R \\ z_R \\ \end{bmatrix} \implies \begin{cases} u = \frac{fx_R}{z_R} + u_0 \\ v = \frac{fy_R}{z_R} + v_0 \end{cases}

Orthographic Projection

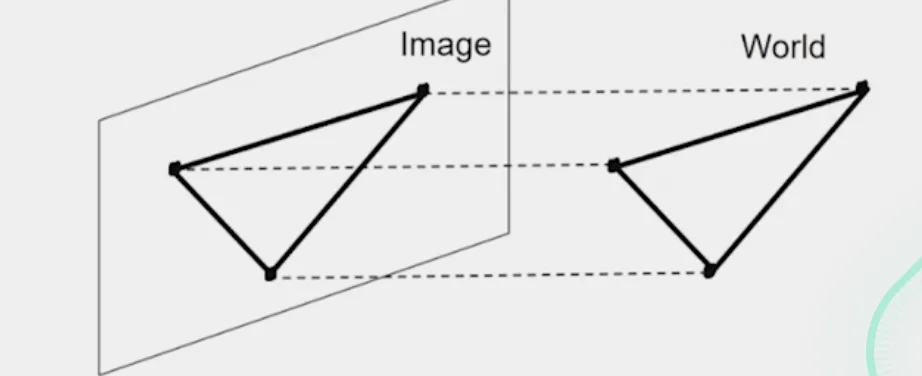
clipboard.png

  • Special case of perspective projection
  • used when the scene is far away or depth variation is small.
  • It assumes parallel projection rays
  • All lines of sight are parallel, not converging.
[uv1]=[100u0010v00001][xyz1]\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & u_0\\ 0 & 1 & 0 & v_0\\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}

Scaled Orthographic Projection

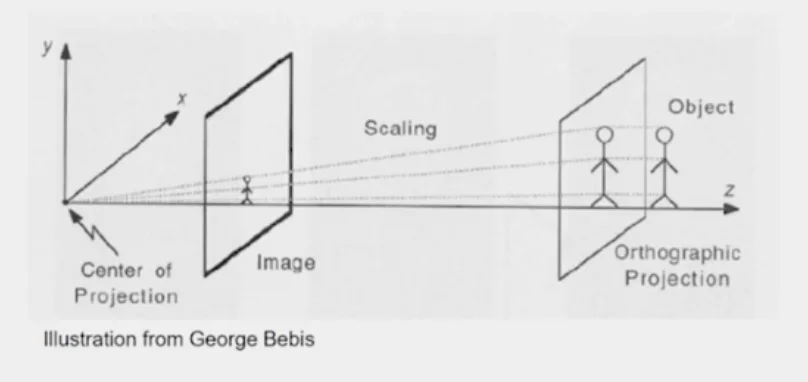
clipboard.png

  • weak perspective
  • Assume that all points in the object are roughly at the same average depth Z0Z_0
  • Perspective effects are approximated by a constant scale factor.
x=sX,y=sYx = sX, \quad y = sY

where

  • s=fZ0s = \frac{f}{Z_0}
[uv1]=[10000100000s][xyz1]\begin{bmatrix} u\\ v\\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & s \end{bmatrix} \begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}

Summary

ModelProjection EquationsNotes
Perspectivex=fXZy=fYZx = \frac{fX}{Z} \\ y = \frac{fY}{Z}Realistic camera model; nonlinear; introduces foreshortening and vanishing points.
Scaled Orthographic (Weak Perspective)x=sXy=sYs=fZ0 x = sX\\ y = sY\\ s = \frac{f}{Z_0}Linear approximation of perspective; assumes small depth variation; preserves shape ratios.
Orthographicx=Xy=Yx = X\\ y = Y \\Simplest linear model; no scaling or depth effect; preserves parallelism and true dimensions.

Tip

Homogeneous coordinates allows 3D world points mapped to 2D image points in a linear way