7.1 Single-view Metrology and Cameras

Review: Projection Matrix

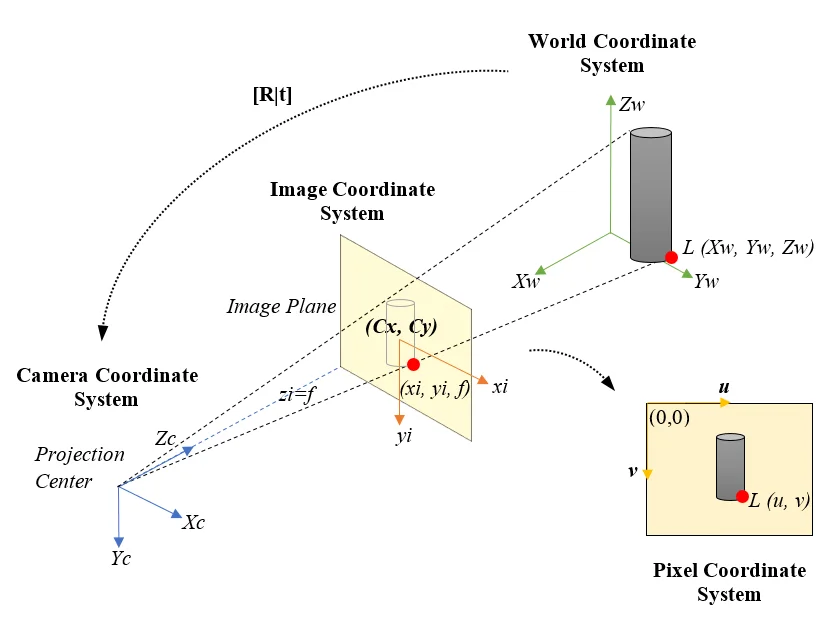
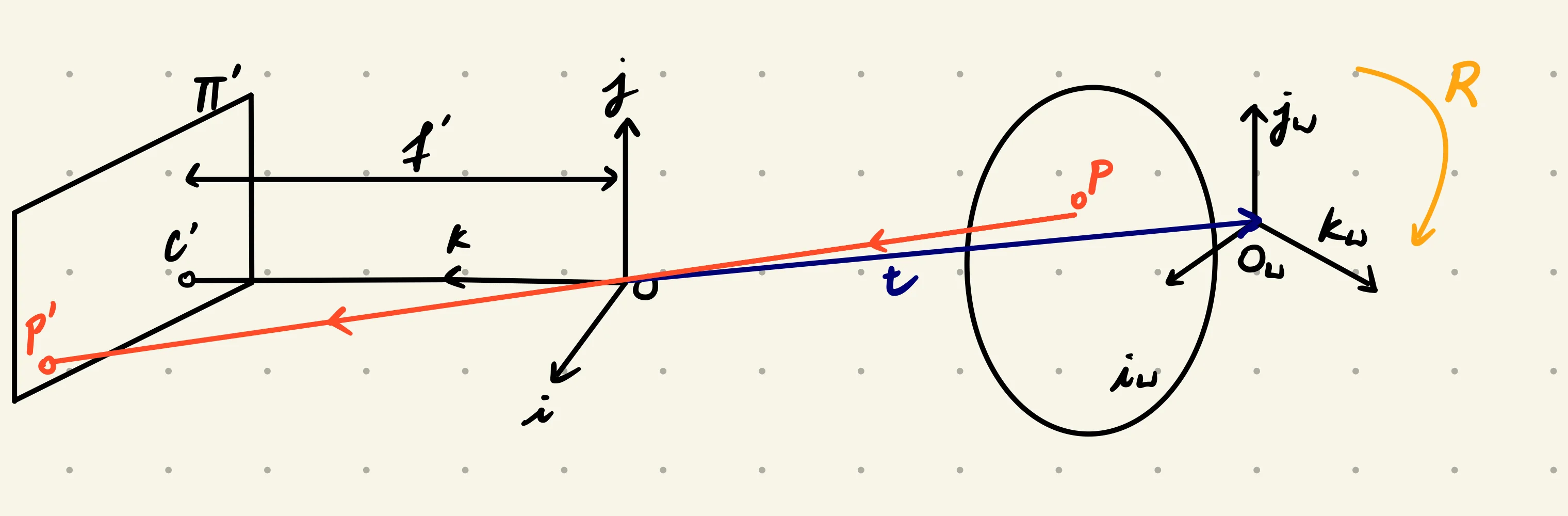
Formula Recap

x = K \left[R \mid t\right]X

where

$X = \begin{bmatrix}X \\ Y \\ Z \\ 1\end{bmatrix}$ $\rightarrow$ 3-D world coordinates
$x = \begin{bmatrix}u \\ v \\ 1\end{bmatrix}$ $\rightarrow$ Image pixel coordinates
$K$ $\rightarrow$ Intrinsic parameters
$R, t$ $\rightarrow$ extrinsic parameters

Matrix Components

$\bullet$ Intrinsic Matrix K:

K = \begin{bmatrix} &f \quad &s \quad &u_0 \\ &0 \quad &\alpha f \quad &v_0 \\ &0 \quad &0 \quad &1 \\ \end{bmatrix}

Parameter	Meaning	Visual Effect
$f$	focal length	controls field of view (zoom in/out)
$s$	skew	shears the image horizontally
$\alpha$	aspect ratio (y-scaling)	stretches/compresses vertically
$(u_0, v_0)$	principal point	shifts the image center

$\bullet$ Extrinsic Matrix [R | t]

[R \mid t] = \begin{bmatrix} &r_{11} \quad &r_{12} \quad &r_{13} \quad &t_x\\ &r_{21} \quad &r_{22} \quad &r_{23}\quad &t_y \\ &r_{31} \quad &r_{32} \quad &r_{33}\quad &t_z\\ \end{bmatrix}

Parameter	Meaning	Visual Effect
$R$	rotation matrix	rotates the camera view around x, y, z
$t$	translation vector	moves the camera in world space

Take-home Questions

1. Suppose the camera axis is in the direction of (x = 0, y = 0, z = 1) in its own coordinate system. What is the camera axis in world coordinates given the extrinsic parameters R, t

What is the z-direction (the direction the camera is facing) given the rotation and translation matrix?

X^h_c = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} &R_{3\times3} \quad &t_{3\times1} \\ &0 \quad &1 \\ \end{bmatrix} X^h_w \\ where\; X^h_w = \begin{bmatrix}x_w \\ y_w \\ z_w \\ 0\end{bmatrix}

$X_w^h$ is what we want

\begin{align*} &X_c = [R \mid t]\begin{bmatrix}X_w \\ 1\end{bmatrix} \\ &X_c = RX_w + t \\ &X_w = R^{-1}X_c - R^{-1}t \\ &X_w = R^TX_c - R^Tt \\ \end{align*}

The position of the camera is $-R^Tt$
Since $X_c$ is 0, the position of the camera is the world coordinate is $-R^Tt$
At infinity, translation is going to have no effect

\begin{align*} &X_w = R^TX_c \cancel{- R^Tt} \\ &X_w = R^TX_c \\ &X_w = \left[R \quad 0\right] \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix} \\ \end{align*}

$X_w$ is just the $3^{rd}$ column of the transposed rotation matrix

2. Suppose a camera at height $y = h \quad (x = 0, z = 0)$ observes a point at $(u, v)$ known to be on the ground $(y = 0)$ . Assume $R$ is an identity matrix. What is the 3D position of the point in terms of f, $u_0, v_0$

Recall that the position of the camera is $-R^Tt$

\begin{align*} &-R^Tt = \begin{bmatrix}0 \\ h \\ 0\end{bmatrix} \quad \text{(Given in the question)} \\ &-t = \begin{bmatrix}0 \\ h \\ 0\end{bmatrix} \quad \text{(R is an Identity matrix)} \\ &t = \begin{bmatrix}0 \\ -h \\ 0\end{bmatrix} \\ \end{align*}

Now calculate the point in the camera’s coordinate, assuming that we know the intrinsic parameters

\begin{align*} X_c &= [R \mid t] \begin{bmatrix}X_w \\ 1\end{bmatrix} \quad \text{(points at the camera's coordinate)} \\ &= X_w + \begin{bmatrix}0 \\ -h \\ 0\end{bmatrix} \\ w \begin{bmatrix}u \\ v \\ 1\end{bmatrix}&= K \left[X_w + \begin{bmatrix}0 \\ -h \\ 0\end{bmatrix}\right] \quad (\text{Image coordinate})\\ \end{align*}

Given that $K = \begin{bmatrix} &f \quad &0 \quad &u_0 \\ &0 \quad & f \quad &v_0 \\ &0 \quad &0 \quad &1 \\ \end{bmatrix}$ and $X_w = \begin{bmatrix}x_w \\ 0 \\ z_w\end{bmatrix} \quad (\text{on the ground})$

\begin{align*} w \begin{bmatrix}u \\ v \\ 1\end{bmatrix}&= K \left[X_w + \begin{bmatrix}0 \\ -h \\ 0\end{bmatrix}\right] \quad (\text{Image coordinate})\\ K^{-1}w \begin{bmatrix}u \\ v \\ 1\end{bmatrix}&= X_w + \begin{bmatrix}0 \\ -h \\ 0\end{bmatrix} \\ K^{-1}w \begin{bmatrix}u \\ v \\ 1\end{bmatrix}&= \begin{bmatrix}x_w \\ -h \\ z_w\end{bmatrix} \\ \end{align*}

Given that $K^{-1} = \begin{bmatrix} \frac{1}{f_x} & 0 & -\frac{c_x}{f_x}\\ 0 & \frac{1}{f_y} & -\frac{c_y}{f_y}\\ 0 & 0 & 1 \end{bmatrix}$

\begin{align*} &w \left(\frac{u}{f} - \frac{u_0}{f}\right) = x_w \\ &w \left(\frac{v}{f} - \frac{v_0}{f}\right) = -h \\ &w = z_w \end{align*}

Takeaway

You have the following two equations to solve various kinds of problems

\begin{align*} &X_c = [R \mid t]\begin{bmatrix}X_w \\ 1\end{bmatrix} \\ &\text{The position of the camera is }-R^Tt \\ &w \begin{bmatrix}u \\ v \\ 1\end{bmatrix}= K \left[X_w + \begin{bmatrix}0 \\ -h \\ 0\end{bmatrix}\right] \quad (\text{Image coordinate})\\ \end{align*}

How to calibrate the camera?

Height Measurement

Objects along the same parallel lines are of the same height

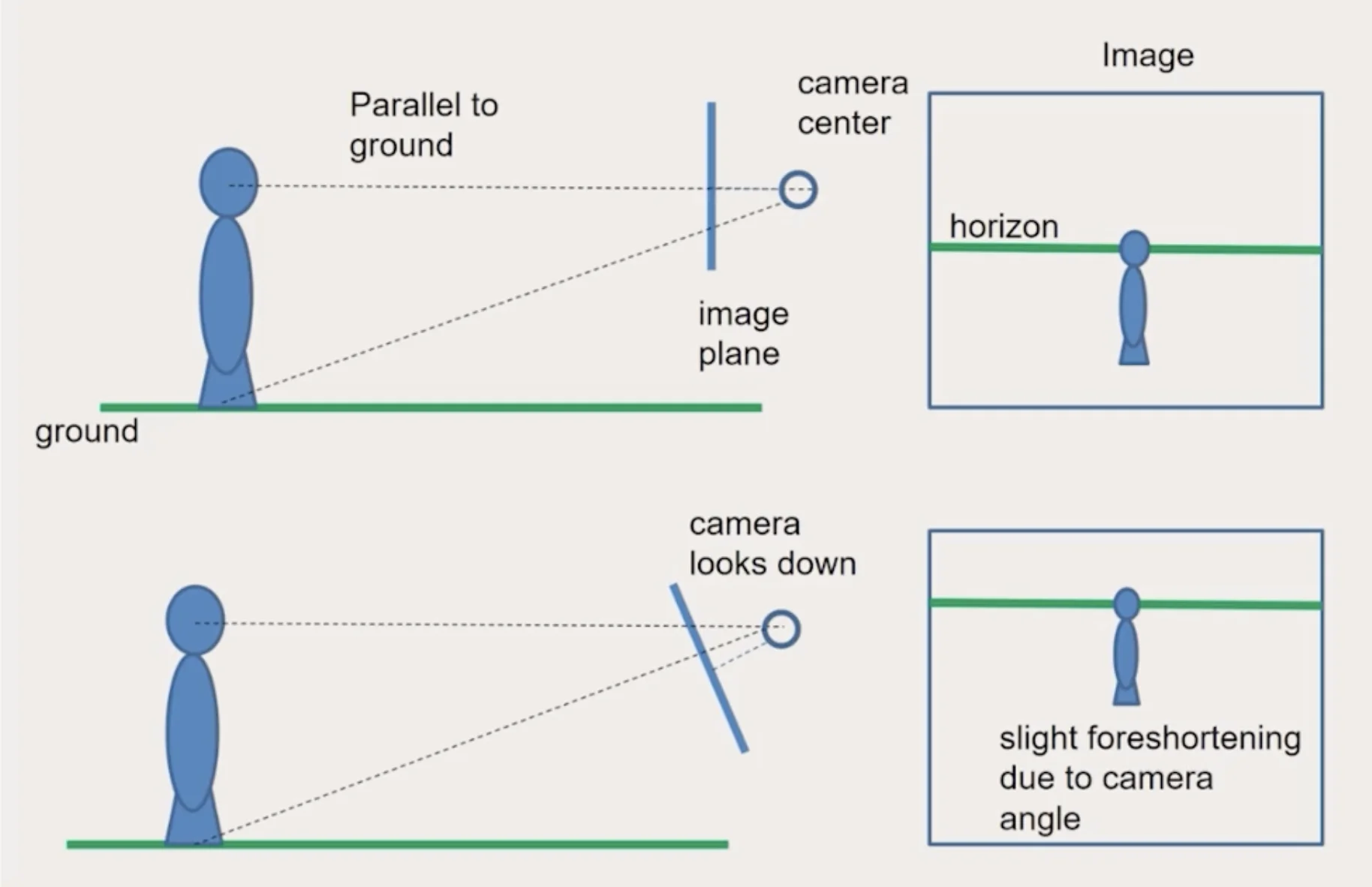
Camera height is the height of horizon
Parachute is higher than the camera while the person is than the camera

Cross Ratio

\frac{||P_3 - P_1|| \times ||P_4 - P_2||}{||P_3 - P_2|| \times ||P_4 - P_1||}

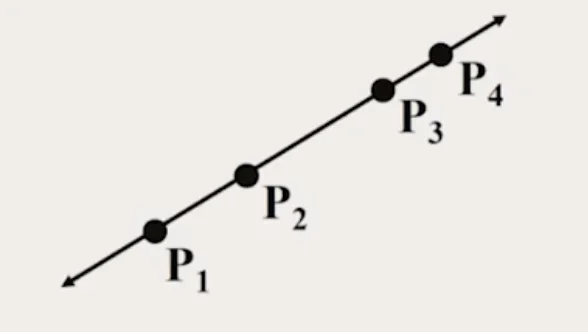
Projective invariant

\underbrace{\frac{||B - T|| \times ||\infty - R||}{||B - R|| \times || \infty -T||}}_{\text{Scene-cross Ratio}} = \underbrace{\frac{||b - t|| \times ||v_z - r||}{||b - r|| \times || v_z - t||}}_{Image-cross Ratio} = \frac{H}{R}

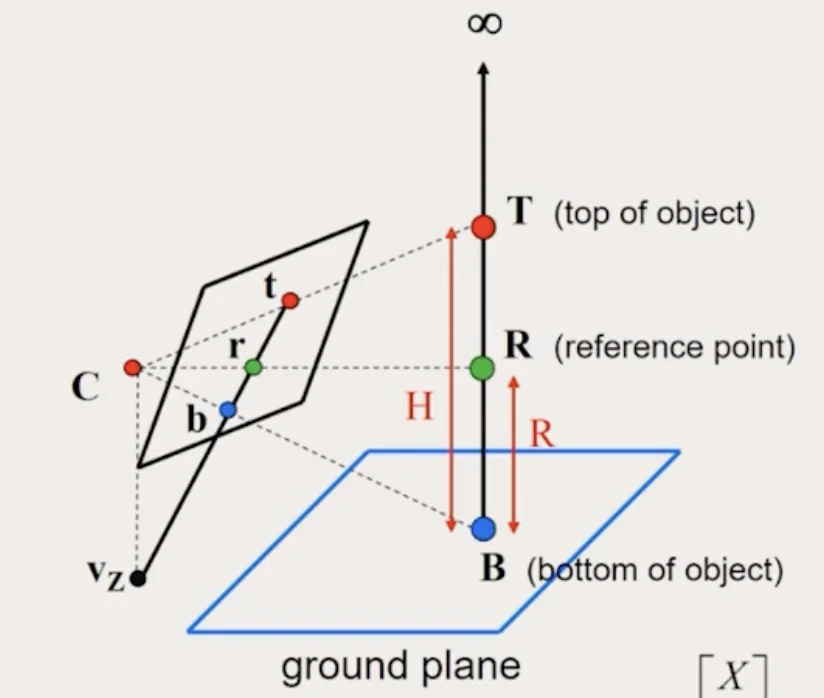
Example: The height of the man

\underbrace{\frac{||t - b|| \times ||v_z - r||}{||r - b|| \times || v_z - t||}}_{Image-cross Ratio} = \frac{H}{R}

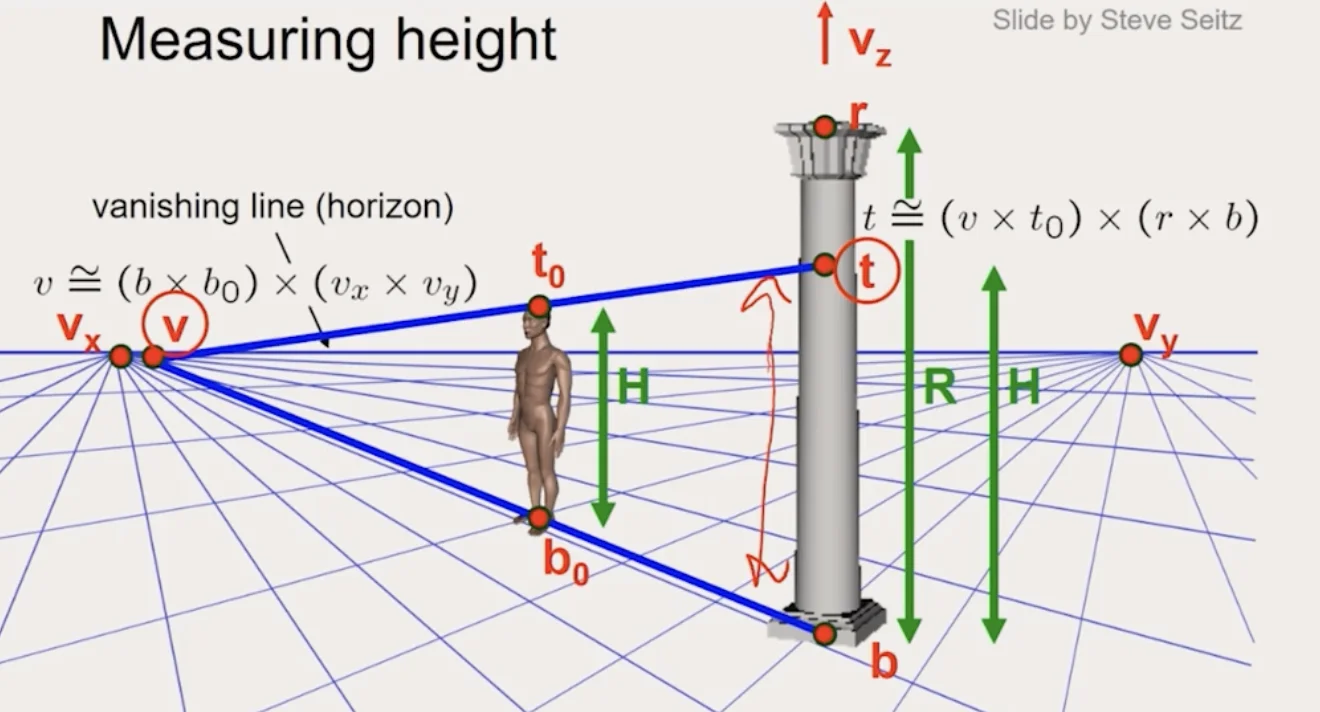
Lens, Aperture, and DOF

Goal (What We Want)	How We Get It	Effect / Explanation	Cost / Trade-off
More spatial resolution	Increase focal length (zoom in)	Magnifies the subject; effectively increases detail on the sensor	Reduces light reaching the sensor, narrows field of view (FOV)
	Decrease focal length (wider lens)	Captures more area; lower magnification	Reduces depth of field (DOF); less background separation
Broader field of view	Decrease focal length (wide-angle lens)	Captures a wider scene	Decreases DOF; may introduce distortion
More depth of field (DOF)	Decrease aperture (smaller opening → larger f-number)	Increases range of sharp focus from near to far	Reduces light; requires longer exposure or higher ISO
	Increase aperture (larger opening → smaller f-number)	Decreases DOF, isolates subject with background blur	Gains light but loses focus range (shallow DOF)
More temporal resolution	Shorten exposure time	Freezes fast motion; captures more frames per second	Reduces light; image may be underexposed
	Lengthen exposure time	Increases light collection; motion blur can appear	Reduces temporal resolution (motion blur)

Quick Reference — Aperture Effects

Aperture Type	Description	Depth of Field	Light Intake	Typical Use
Large aperture (small f-number, e.g., f/1.8)	Wide lens opening	Shallow DOF (background blur)	More light	Portraits, low-light photography
Small aperture (large f-number, e.g., f/16)	Narrow lens opening	Deep DOF (sharp foreground + background)	Less light	Landscapes, daylight scenes

Warning

The effect will not be great if the aperture is too small as you may encounter issues related to diffraction

Comprehensive List for Adjusting All the Camera Parameters

Parameter	What It Controls	If You Increase It	If You Decrease It	Affects Field of View (FOV)?	Affects Depth of Field (DOF)?	Other Key Effects
Aperture (f-stop ↓)	Lens opening size	Larger opening → more light (brighter image) Shallower DOF (blurred background)	Smaller opening → less light (darker image) Deeper DOF (more in focus)	❌ No	✅ Strongly	Controls exposure and background blur
Shutter Time	Duration sensor is exposed to light	Longer → more light Motion blur increases	Shorter → less light Motion frozen	❌ No	❌ No	Controls motion blur and brightness
Focal Length	Lens zoom / magnification	Narrows FOV (zoom in) Shallower DOF	Widens FOV (zoom out) Deeper DOF	✅ Yes	✅ Yes	Affects perspective compression
ISO Sensitivity	Sensor’s light sensitivity	Brighter image More noise/grain	Darker image Cleaner image	❌ No	❌ No	Trade-off between brightness and noise
Sensor Size	Physical size of the imaging sensor	Wider FOV (for same focal length) Shallower DOF	Narrower FOV Deeper DOF	✅ Yes	✅ Yes	Larger sensors perform better in low light
Focus Distance	Distance to subject	Focusing closer → shallower DOF	Focusing farther → deeper DOF	❌ No	✅ Yes	Macro shots have very thin DOF
Exposure (Overall)	Total light hitting the sensor	Increased by aperture ↑, shutter ↑, or ISO ↑	Decreased by aperture ↓, shutter ↓, or ISO ↓	❌ No	Indirectly	Determines image brightness

Key Takeaways

Concept	Definition	Main Controls	Typical Use
Field of View (FOV)	How much of the scene is captured in the frame	Focal length, sensor size	Wide landscape vs. zoomed portrait
Depth of Field (DOF)	How much of the depth range appears in focus	Aperture, focal length, focus distance, sensor size	Portraits (shallow) vs. landscapes (deep)
Exposure	Brightness of the image	Aperture, shutter time, ISO	Properly balanced image

13. Single-view Metrology and Cameras

7.1 Single-view Metrology and Cameras

Review: Projection Matrix

Formula Recap

Matrix Components

∙\bullet∙ Intrinsic Matrix K:

∙\bullet∙ Extrinsic Matrix [R | t]

Take-home Questions

1. Suppose the camera axis is in the direction of (x = 0, y = 0, z = 1) in its own coordinate system. What is the camera axis in world coordinates given the extrinsic parameters R, t

2. Suppose a camera at height y=h(x=0,z=0)y = h \quad (x = 0, z = 0)y=h(x=0,z=0) observes a point at (u,v)(u, v)(u,v) known to be on the ground (y=0)(y = 0)(y=0). Assume RRR is an identity matrix. What is the 3D position of the point in terms of f, u0,v0u_0, v_0u0​,v0​

Takeaway

How to calibrate the camera?

Height Measurement

Cross Ratio

Example: The height of the man

Lens, Aperture, and DOF

Quick Reference — Aperture Effects

Comprehensive List for Adjusting All the Camera Parameters

Key Takeaways

$\bullet$ Intrinsic Matrix K:

$\bullet$ Extrinsic Matrix [R | t]

2. Suppose a camera at height $y = h \quad (x = 0, z = 0)$ observes a point at $(u, v)$ known to be on the ground $(y = 0)$ . Assume $R$ is an identity matrix. What is the 3D position of the point in terms of f, $u_0, v_0$