Contrast Enhancement

Luminance

a photometric measure of the phtometric measure of the luminous intensity per unit area of light traveling a given direction
Luminance leves indicate the amount of luminous power that is detectable to human eyes froma a particular surface and angle of view.

Formulation

The luminance of a specified point of a light source, in a specified direction, is defined by:

L_v = \frac{d^2 \Phi_v}{d \sum d\Omega_{\sum} cos\theta_{\sum}}

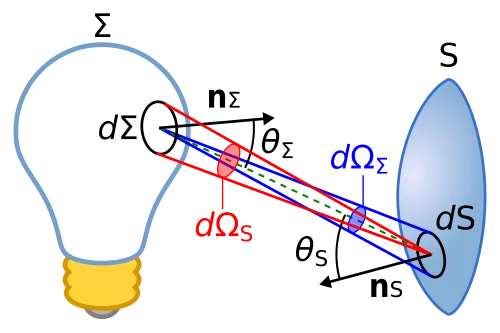
Step 1: What are the symbols?

$\Phi_v$ : Radiant flux (power of visible light in photometry, measured in lumens). More generally, in radiometry, $\Phi$ is the radiant flux (watts).
$d^2 \Phi_v$ : An infinitesimal amount of flux, considered with respect to both area and solid angle.
$\Sigma$ (sometimes written $A$ ): The surface area element through which radiation is passing.
$d\Omega_{\Sigma}$ : The differential solid angle subtended by the ray bundle at the surface element. A solid angle is measured in steradians (sr).
$\theta_{\Sigma}$ : The angle between the surface normal of the patch $d\Sigma$ and the incoming (or outgoing) light direction.
$\cos\theta_{\Sigma}$ : A projection factor that accounts for foreshortening. A patch tilted away from the ray captures less flux than one directly facing it.
$L_v$ : The luminance (photometric equivalent of radiance). Units:

\text{cd/m}^2 = \frac{\text{lm}}{\text{m}^2 \cdot \text{sr}}

(candelas per square meter).

Step 2: Meaning of the denominator

$d\Sigma \cos\theta_{\Sigma}$ is the projected area of the surface as “seen” from the light’s direction. This projection ensures that grazing angles collect less light.
$d\Omega_{\Sigma}$ expresses in which direction the light is traveling (the angular spread of the beam).

So the denominator is:

d\Sigma \cos\theta_{\Sigma} \, d\Omega_{\Sigma}

“the projected area of the patch times the solid angle of the beam.”

Step 3: Putting it together

The formula says:

L_v = \frac{\text{flux in a given beam}}{\text{projected area} \times \text{solid angle of that beam}}

So luminance (radiance) is the flux density per projected area per unit solid angle.

Step 4: Intuition

Imagine a tiny surface element $d\Sigma$ .
Pick a direction at angle $\theta$ .
Through a tiny cone of solid angle $d\Omega$ around that direction, some small flux $d^2 \Phi$ passes.
The formula says: luminance is the “concentration of flux” in that specific direction per unit projected area.

That’s why luminance (or radiance, in radiometry) is considered directional brightness: it’s not just “how much flux,” but “how much flux in a given direction per surface orientation.”

✅ Summary: This is the definition of luminance (photometric radiance). It relates radiant flux to geometry and direction:

$d^2 \Phi_v$ : how much light leaves/arrives.
Divided by $d\Sigma \cos\theta$ : accounts for the orientation of the surface.
Divided by $d\Omega$ : distributes the flux over angular spread.

That’s why luminance is the fundamental measure of brightness that stays invariant along rays in a lossless medium.

Gamma Correction

Nonlinear mapping of pixel intensities that adjusts how brightness and contrast are perceived

I_{out} = I_{in}^\gamma

where:

$I_{in}:$ input pixel value (normalized to $[0, 1]$ )
$I_{out}:$ output pixel value
$\gamma \in \R^+$

$\bullet$ Effect of $\gamma$

\gamma \Rightarrow \begin{cases} \text{Brightens the image} &\quad\quad (\gamma < 1) \\ \text{Darkens the image} &\quad\quad (\gamma > 1) \\ \text{No change} &\quad\quad (\gamma = 1) \end{cases}

Note

This works because our eyes perceive brightness niina nonlinear way. Gamma correction compensates for that and helps adjust images for human viewing

$\bullet$ Why does it work?

1. Light vs. Human Perception

Light intensity is linear. Doubling the number of photons doubles the physical brightness
Human vision is non-linear as our eyes are more sensitive in dark regions than in bright regions
$10 \rightarrow 20:$ A big jump
$210 \rightarrow 220:$ Not much of a difference

2. Gamma Mapping

# Draw gamma correction curves for multiple gamma values
import numpy as np
import matplotlib.pyplot as plt

# Input intensity (normalized 0..1)
x = np.linspace(0, 1, 1001)

gammas = [0.3, 0.5, 0.8, 1.0, 1.5, 2.2, 3.0]

plt.figure(figsize=(7, 5))
for g in gammas:
 y = x ** g
 plt.plot(x, y, label=f"γ = {g}")

plt.plot([0, 1], [0, 1], linestyle="--", linewidth=1, label="Linear (γ = 1)")

plt.title("Gamma Correction Curves: Output = Input^γ")
plt.xlabel("Input Intensity (normalized)")
plt.ylabel("Output Intensity (normalized)")
plt.xlim(0, 1)
plt.ylim(0, 1)
plt.grid(True, alpha=0.3)
plt.legend(title="Gamma values", loc="best")
plt.show()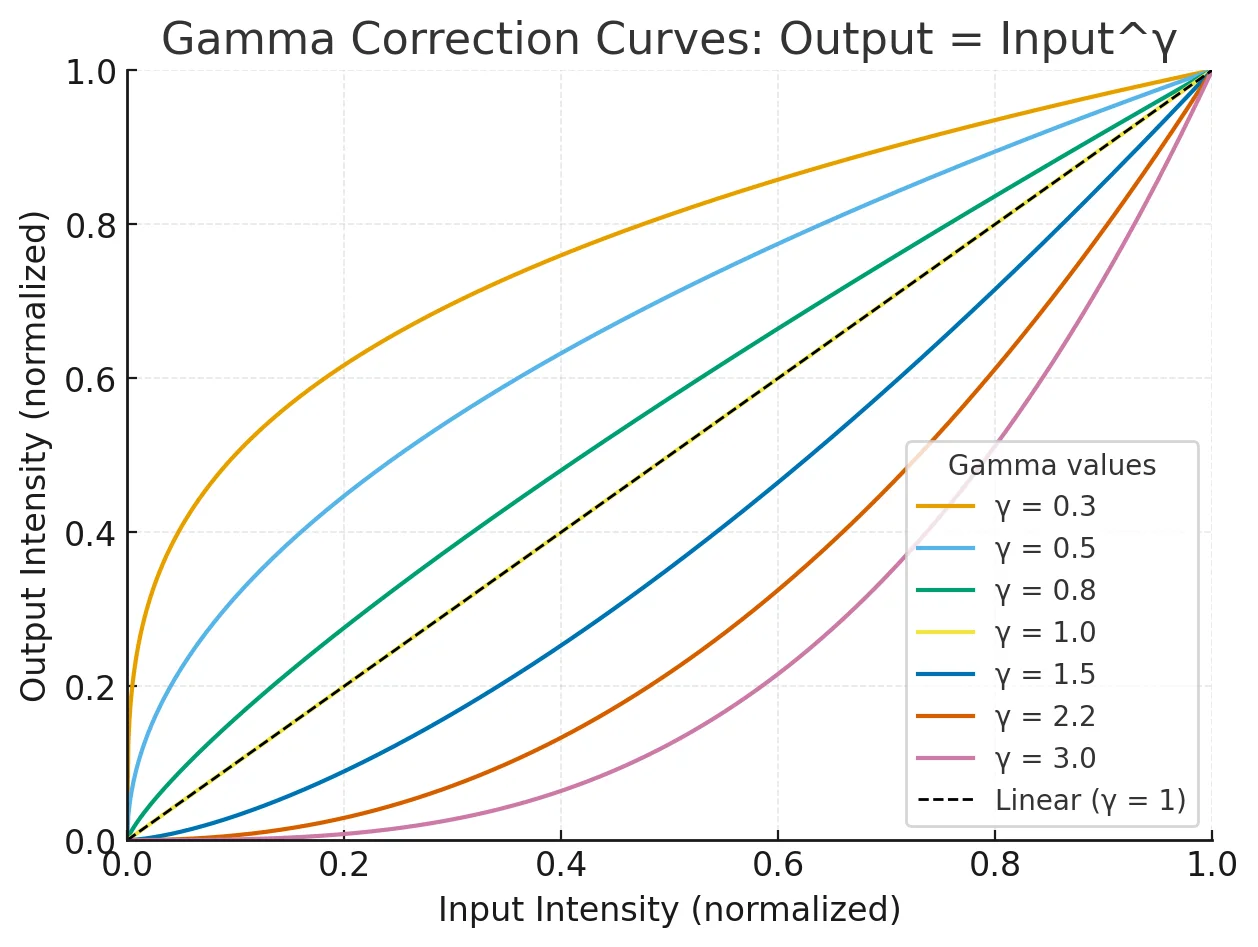

Curves above the diagonal $(\gamma < 1)$

the output is greater than the input
Dark pixels are mapped to brighter values $(0.2 \rightarrow 0.45 \quad (\gamma = 0.5))$

Curves below the diagonal $(\gamma > 1)$

the output is less than the input
Mid/Bright pixels are pushed down $(0.7 \rightarrow 0.4 \quad (\gamma = 2.2))$

Lab: Contrast Enhancement