CH 5.

5-1. Introduction

Caution

It is impossible to access all code and data while keeping memory access fast. Therefore, we need the principle of locality.

What is the principle of locality?

Programs access a small portion of address space at instant time.

Temporal Locality
locality in time
recent accessed addresses may be re-accessed very soon
Spatial Locality
locality in space
addresses near recent the accessed address may be accessed very soon

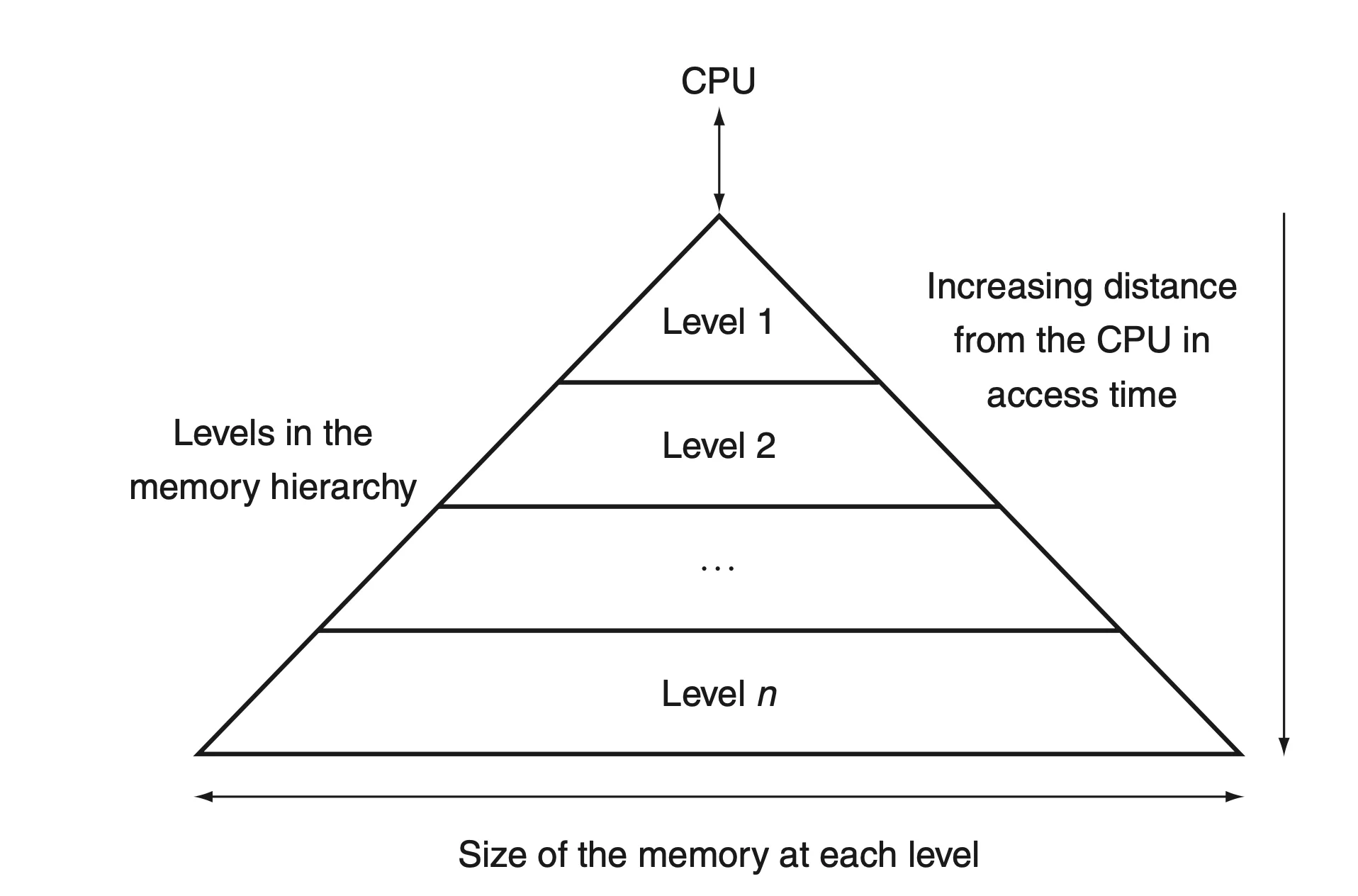
Memory Hierarchy

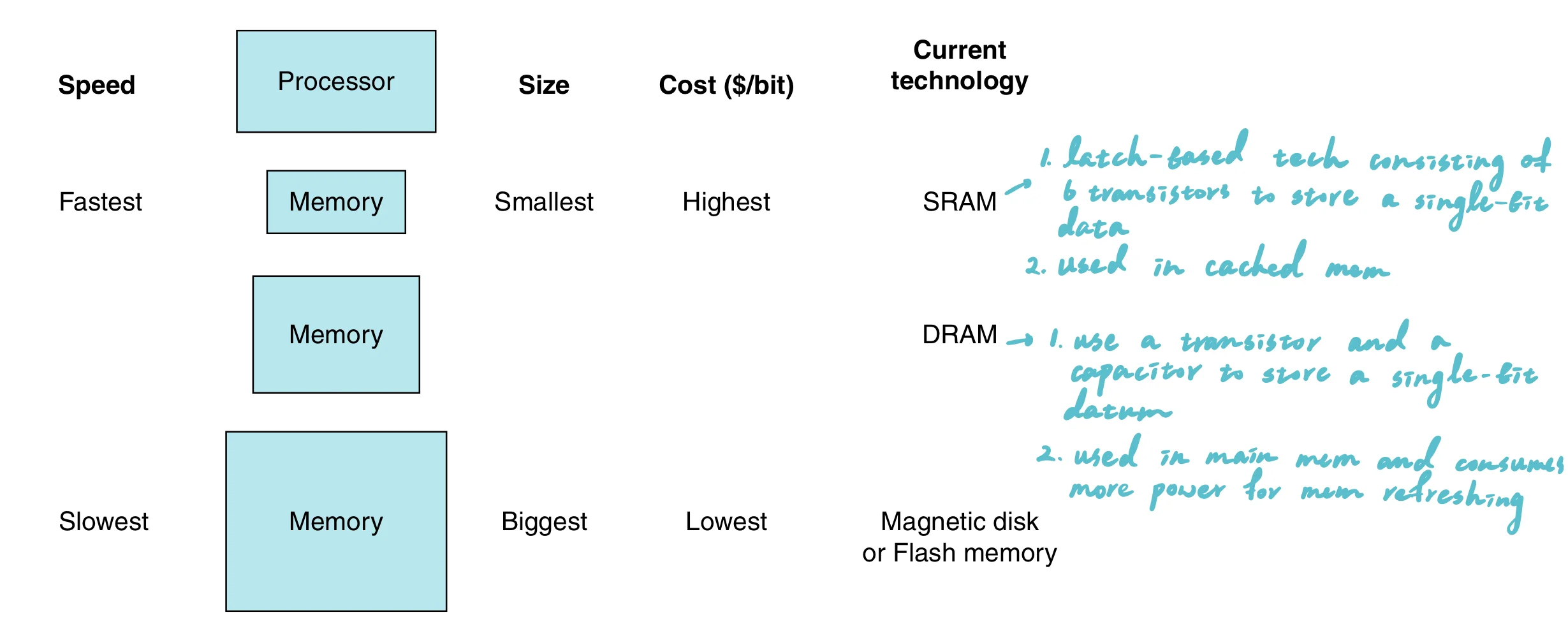
Faster memory is closer to the processor
Present as much memory as possible in the cheapest memory tech

Terminologies

hit: the required address is found in upper level memory
hit rate: the fraction of memory access found
hit time: the time required to access upper level memory
miss: the required address is not found in upper level memory
miss rate: the fraction of memory access not found
miss penalty: the time to replace upper level memory with required address found in the lower level memory

Note

Memory hierarchies take advantage of temporal locality.

Memory hierarchies, such as cache memories, are designed to keep recently accessed data closer to the processor to speed up subsequent accesses.

On a read, the value returned depends on which blocks are in the cache.

If the required data is found in the cache (a cache hit), the value is quickly returned from the cache. If it is not in the cache (a cache miss), the memory hierarchy must fetch the data from a lower, slower level (like main memory), and this value is then returned.

The lowest level of the memory hierarchy usually has the largest capacity.

This is because slower storage technologies tend to be cheaper per bit stored and are used to store the bulk of the data that does not require fast access speeds.

5.2 Memory Technology

SRAM and DRAM

SRAM (Static Random Access Memory) and DRAM (Dynamic Random Access Memory) are both types of RAM (Random Access Memory), used primarily in computers and other electronic devices for temporary data storage. Here are the key differences between the two:

Feature	DRAM	SRAM	SDRAM
Full Form	Dynamic Random Access Memory	Static Random Access Memory	Synchronous Dynamic Random Access Memory
Speed	Slower than SRAM	Faster than DRAM	Faster than DRAM, synchronized with system bus
Cost per Bit	Lower	Higher	Moderate, higher than DRAM but less than SRAM
Power Consumption	Higher due to refresh cycles	Lower (no refresh needed)	Moderate, efficient due to synchronization
Complexity	Simpler (1 transistor, 1 capacitor per bit)	Complex (6 transistors per bit)	Like DRAM, but includes additional logic for synchronization
Usage	Main system memory	Cache memory in CPUs and high-speed storage areas	Main system memory, often used in PCs and servers
Density	High	Low	High
Volatility	Volatile (needs power to maintain data)	Volatile (needs power to maintain data)	Volatile (needs power to maintain data)

Hamming Code (SEC/DED)

Overview

The Hamming Code (SEC/DED) is used for error detection and correction, specifically designed to correct single-bit errors and detect double-bit errors in data bits transmitted or stored in computer systems.

Functionality

Single Error Correction (SEC): Corrects any single-bit error within a block of data.
Double Error Detection (DED): Detects the presence of two errors within the same block of data.

Mechanism

Data is encoded with additional bits called parity bits, placed at positions that are powers of two (1, 2, 4, 8,…).
Each parity bit calculates the parity (even or odd sum) for groups of bits under its coverage. Coverage is determined by the binary representation of the bit positions (e.g., parity bit at position n covers all bit positions including n in their binary form).

Example

Consider a 4-bit data: 1011. To apply Hamming SEC/DED:

Position Parity Bits: Insert parity bits (P) at positions 1, 2, and 4.

P1 _ P2 1 P4 0 1 1 (P1, P2, P4 are parity bits; underscores show their positions)

Calculate Parities:

P1 covers positions 1, 3, 5, 7 (bits are P1, 1, 0, 1). Set P1 to make even parity.
P2 covers positions 2, 3, 6, 7 (bits are P2, 1, 1, 1). Set P2 to make even parity.
P4 covers positions 4 to 7 (bits are P4, 0, 1, 1). Set P4 to make even parity.

Encoded Data:

Assuming even parity calculation, encoded sequence might be 0 11 1 0 1 1 where 0, 1, 1 are the calculated parity bits at positions 1, 2, 4 respectively.

Usage

Memory Systems: Protects against bit flips in memory chips.
Data Transmission: Ensures data integrity in noisy communication channels.

1. Chapter 5