1-1. Nonparametric Methods

Introduction

Parametric methods

  • use of probability distributions that have specific functional forms governed by a small number of parameters whose values are to be determinied from a data set.

Caution

LIMITATION

  • The chosen density might be a poor model of the distribution that generates the data resulting in poor predictive performance
  • Gaussian distribution cannot capture multimodal data

Nonparametric Methods

  • Consider a case of a single continuous variable xx.
  • Using a standard historgrams to partition xx into distinct bins:
  • ii: index of bin
  • Δi\Delta_i: width of bins
  • nin_i: the number of xx falling in bin ii

∙\bullet Normalized Probability Density

  • The bins to obtain probability values:
pi=niNΔip_i = \frac{n_i}{N\Delta_i}
  • Where:
  • ∫p(x)dx=1\int p(x) dx = 1
  • Δi=Δ\Delta_i = \Delta

∙\bullet Example - Histogram

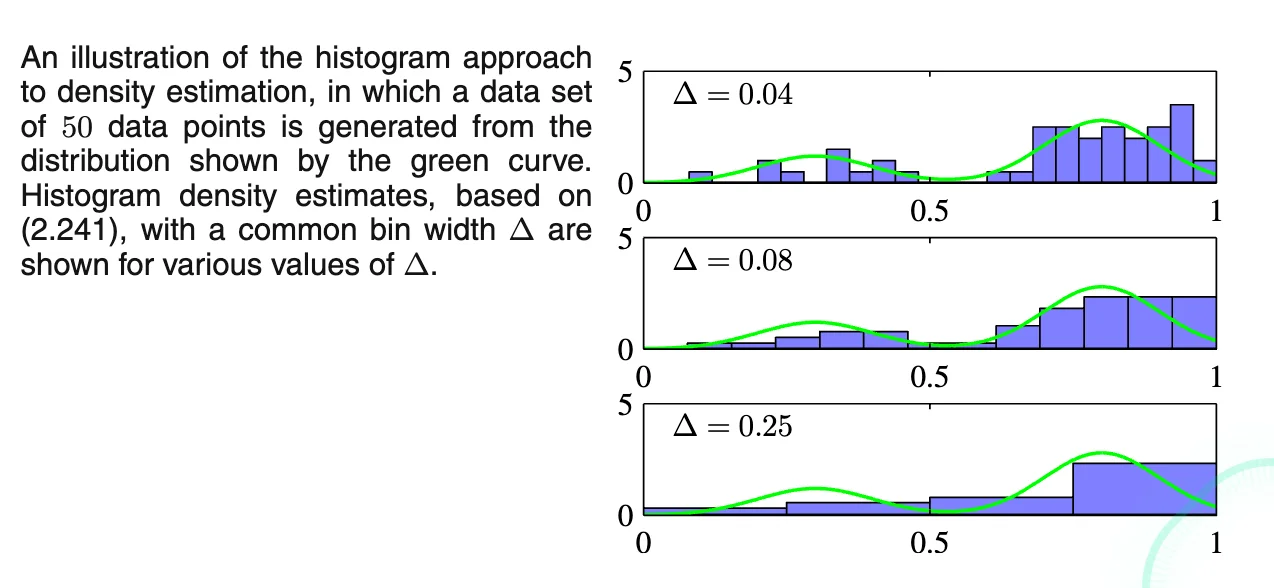
clipboard.png

  • Data is formed from a mixture of 2 Gaussians
  • small Δ\Delta
  • with a lot of structure that is not present in the underlying distribution
  • large Δ\Delta
  • fails to capture the bimodal property

Tip

ADVANTAGES

  • Data set can be discarded after histogram is generated
  • Easily applicable if data points arrive sequentially

Caution

LIMITATION

  • Discontinuities occur due to bin edges rather than the properties of underlying distributions
  • When data are in a high-dimensional space, we would experience

∙\bullet Takeaway from Histogram

  1. Consider the points lie in local neighborhoods (the bins in histogram)
  • Some distance measurements are required
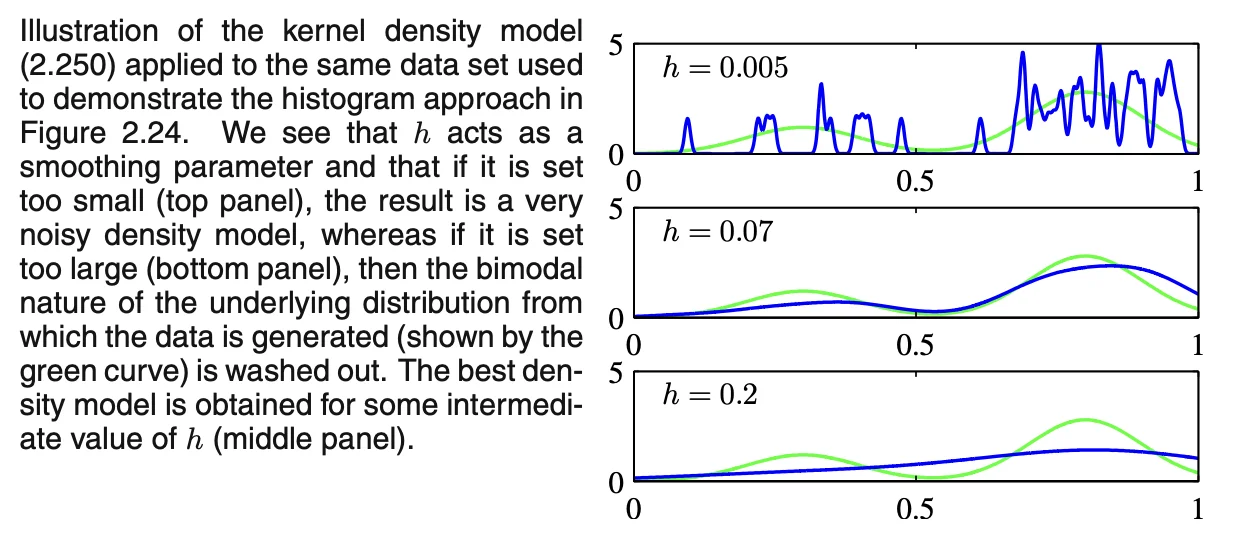
  1. Smoothing parameter should be neither too large nor too small.

Kernel Estimator

  • Assume observations are drawn from a probability density p(x)p(x) in D-dimensional space.
  • Consider a small region RR containing xx

∙\bullet The probability associated with the region RR

P=∫Rp(x)dxP = \int_R p(x) dx

∙\bullet The probability distribution of the total number of K points falling within the region RR

Bin(K∣N,P)=N!K!(N−K)!PK(1−P)N−KBin(K \mid N, P) = \frac{N!}{K!(N - K)!} P^K (1-P)^{N - K}

∙\bullet For large N, the peak is around the mean of K

∵Bin(N,P)⇒μ=NP,σ2=NP(1−P)\because Bin(N, P) \Rightarrow \mu = NP, \sigma^2 = NP(1-P) ∴Var[KN]=1N2Var[K]=1N2NP(1−P)=P(1−P)N\begin{align*} \therefore Var[\frac{K}{N}] &= \frac{1}{N^2}Var[K] \\ &= \frac{1}{N^2}NP(1-P) \\ &= \frac{P(1-P)}{N} \end{align*}

Important

Mean of KK (the count)

E[K]=NP\mathbb{E}[K] = NP

Mean of K/NK/N (the fraction)

E[KN]=P\mathbb{E}[\frac{K}{N}] = P
N→∞,Var→0K≈NP\begin{align*} & N \rightarrow \infty, Var \rightarrow 0 \\ & K \approx NP \end{align*}

∙\bullet If RR is sufficiently small

P≈p(x)VP \approx p(x)V
  • where VV is the volume of RR

∙\bullet Combine KK and PP

K≈NP⇒P≈KN\begin{align*} &K \approx NP \\ &\Rightarrow P \approx \frac{K}{N} \\ \end{align*} P≈p(x)V⇒KN≈p(x)V⇒p(x)≈KNV\begin{align*} &P \approx p(x)V \\ &\Rightarrow \frac{K}{N} \approx p(x)V \\ &\Rightarrow p(x) \approx \frac{K}{NV} \end{align*}

∙\bullet Different Exploitations of p(x)≈KNVp(x) \approx \frac{K}{NV}

Fix K, determine V

  • KNN density estimator

Fix V, determine K

  • Kernel Approach

Note

Both converge to the true probability density in the limit N→∞N \rightarrow \infty with VV shrinking with NN, and KK growing with NN

Kernel Method

  • Take the region RR to be a small hypercube centered on the point xx

  • xx is the point where we wanna determine the probability density.

k(u)={1,∣ui∣≤12,i=1,…,D,0,otherwisek(\mathbf{u}) = \begin{cases} 1, & |u_i| \leq \tfrac{1}{2}, \quad i = 1, \ldots, D, \\[6pt] 0, & \text{otherwise} \end{cases}
  • helps to count the # of KK points falling within RR
  • represents a unit cube centered on the origin
  • k(u)k(\mathbf{u}) is a kernel function called Parzen Window
k(x−xnh)=1k(\frac{x - x_n}{h}) = 1

  • if xnx_n in a cube of side hh centered on x, and 0 otherwise

  • Total # of the datapoints in cube

K=∑n=1Nk(x−xnh)K = \sum_{n = 1}^{N} k (\frac{x - x_n}{h})
  • Swap the total into probability density with V=hDV = h^D
p(x)=1N∑n=1N1hDk(x−xnh)p(x)= \frac{1}{N}\sum_{n = 1}^{N} \frac{1}{h^D} k (\frac{x - x_n}{h})
  • To prevent artificial discontinuities, we can user smoother kernel functions (i.e. Gaussian)
p(x)=1N∑n=1N12πh2e(∣∣x−xn∣∣22h2)p(x)= \frac{1}{N}\sum_{n = 1}^{N} \frac{1}{\sqrt{2\pi h^2}} e^ {(\frac{||x - x_n||^2}{2h^2}})
  • hh is the standard deviation

Screenshot 2025-09-04 at 12.48.39

Tip

  • Any kernel methods satisfying the following conditions can be chosen.
k(u)≥0,∫k(u)du=1\begin{align*} &k(\mathbf{u}) \ge 0, \\ &\int k(\mathbf{u}) du = 1 \end{align*}
  • No computational cost during the training time

Caution

Kernel approach may lead to over-smoothing due to that the hh parameter governing the kernel width is fixed for all kernels

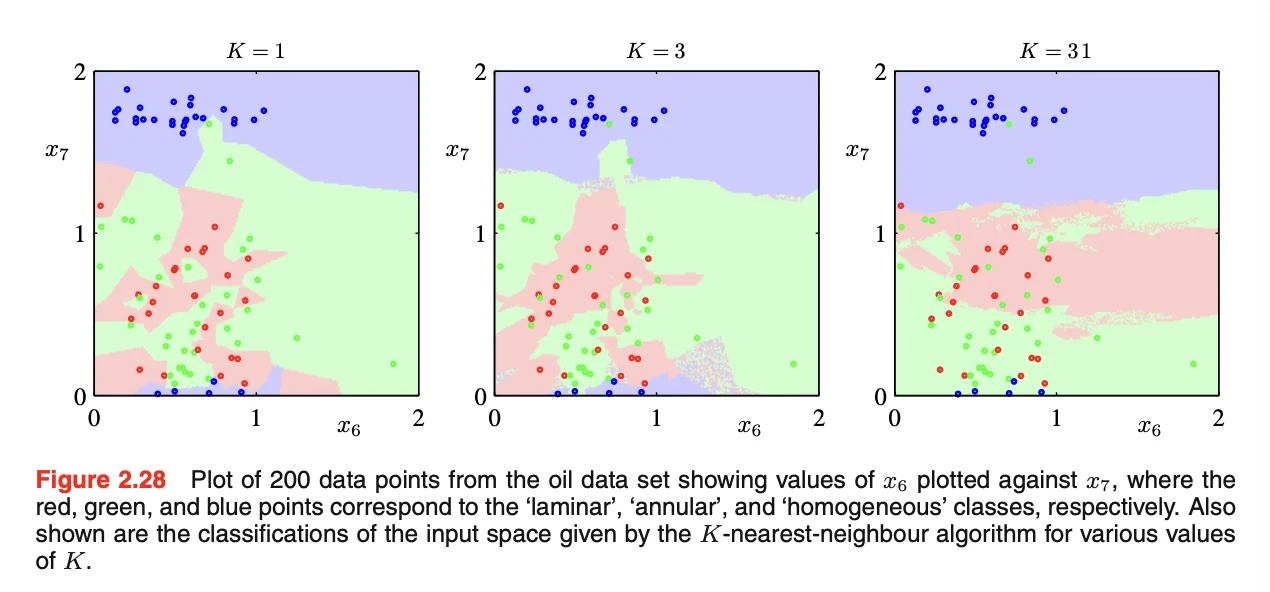
KNN Methods

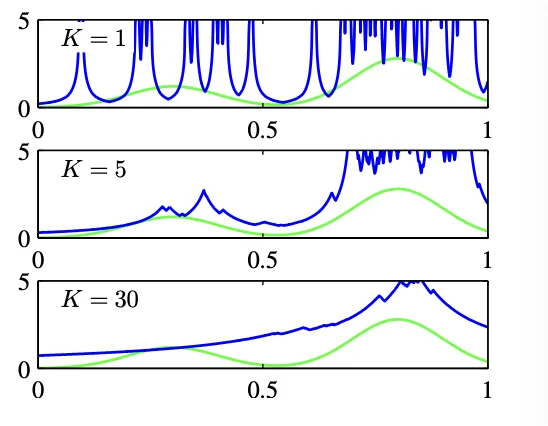
Screenshot 2025-09-04 at 13.03.44

  • The parameter KK governs the degree of smoothing.

Method

  • Assume a data set of sizes NN with NkN_k points in class CkC_k
∑Nk=N\sum N_k = N
  • Draw a sphere centered on a new point xx containing KK points
  • VV: Volume of the sphere
  • KkK_k: points from class CkC_k
  • The estimate of the density associated with each class
p(x∣Ck)=KkNkVp(x \mid C_k) = \frac{K_k}{N_kV}
  • Unconditional Density
p(x)=KNVp(x) = \frac{K}{NV}
  • Priors
p(Ck)=NkNp(C_k) = \frac{N_k}{N}
  • Posteriors
p(Ck∣x)=p(x∣Ck)p(Ck)p(x)=KkNkV⋅NkNKNV=KkK\begin{align*} p(C_k \mid x) &= \frac{p(x \mid C_k)p(C_k)}{p(x)} \\ &= \frac{\frac{K_k}{N_kV} \cdot \frac{N_k}{N}}{\frac{K}{NV}} \\ &= \frac{K_k}{K} \end{align*}

Note

In the case where K = 1, the KNN is called “the nearest-neighbor” approach

Screenshot 2025-09-04 at 13.28.51