1-2 Intro to ML Concepts

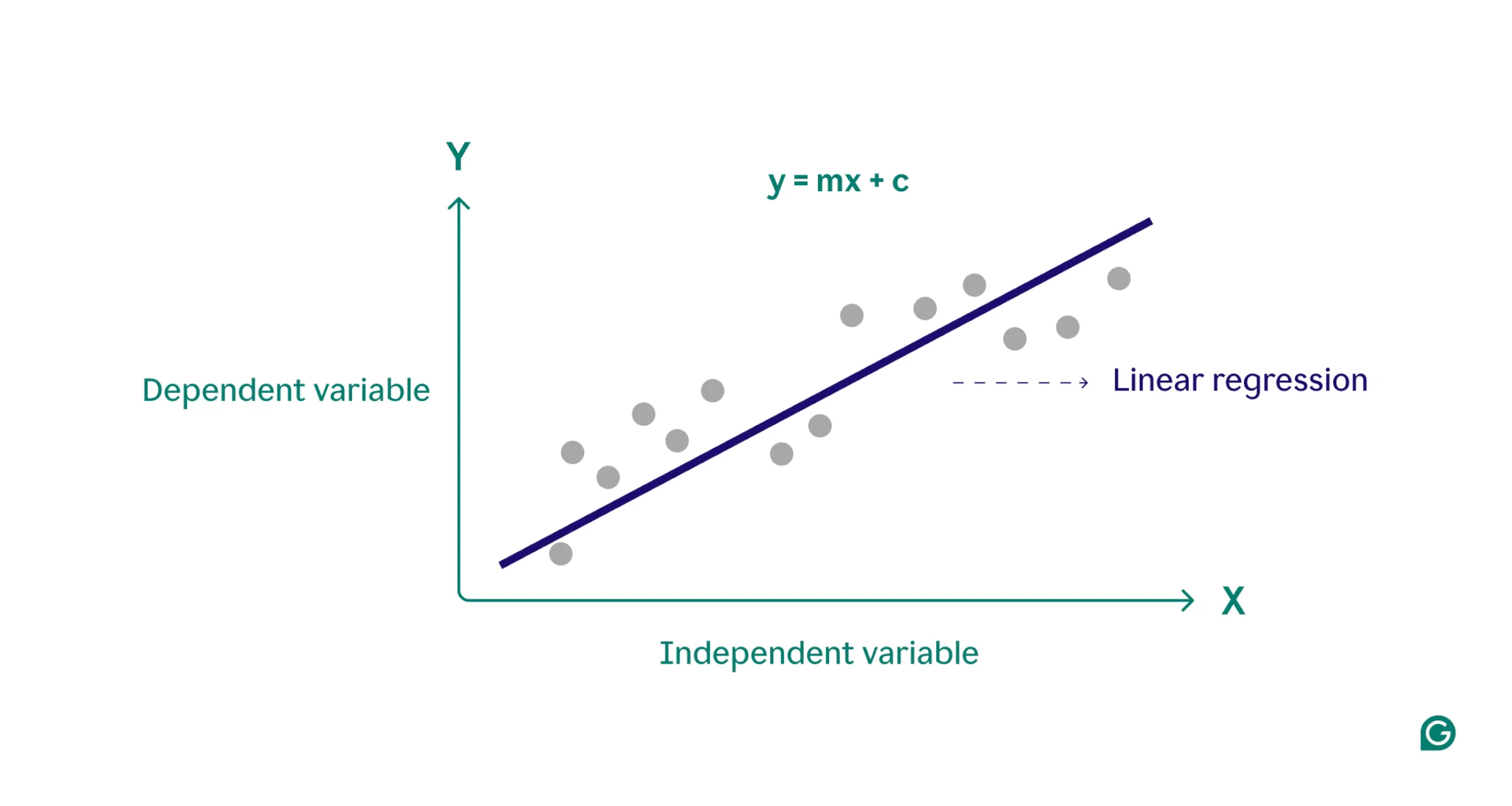
Linear Regression

  • Inductive Bias
  • Assumtptions about the nature of the data distribution
  • p(y∣x)p(y \mid x ) for supervised problem
  • p(x)p(x) for unsupervised problem
  • Parametric Model
  • A statistical model with a fixed number of parameters

∙\bullet Formula for Linear Regression

y(x)=w⊺x+ϵy(x) = w^\intercal x + \epsilon
  • ϵ\epsilon
  • Residual error between our lienar prediction and the true responses
  • ∼N(μ,σ2)\sim{N(\mu, \sigma^2)}

∙\bullet Linear Regression and Gaussian

p(u∣x,θ)=N(y∣μ(x),σ2(x))p(u \mid x, \theta) = N(y \mid \mu(x), \sigma^2(x))
  • μ\mu is a linear function of x s.t. μ=w⊺x\mu = w^\intercal x
  • For 1-D data:
  • μ(x)=w0+w1x=w⊺x\mu(x) = w_0 + w_1x = w^\intercal x
  • σ2(x)\sigma^2(x) is the noise fixed: σ2(x)=σ2\sigma^2(x) = \sigma^2

∙\bullet Estimation via Residual Sum of Squares

  • Objective: minimize the sum of squared residuals
RSS(w)=∑i=1n(yi−w⊤xi)2RSS(w) = \sum_{i=1}^n (y_i - w^\top x_i)^2
  • Optimization Problem
w∗=arg⁡min⁡wRSS(w)w^* = \arg \min_w RSS(w)
  • 2-D Optimization

clipboard.png

  • Formula of RSS
l:y=ax+b(prediction)L=∑i=1n(yi−axi−b)2(RSS)\begin{align*} &l: y = ax + b \quad (prediction)\\ &L = \sum_{i=1}^{n}(y_i - ax_i - b)^2 \quad (RSS) \end{align*}
  • Minimization of RSS
∂L∂a=0∂L∂b=0\frac{\partial L}{\partial a} = 0 \quad\quad \frac{\partial L}{\partial b} = 0 \quad\quad ∂∂a=∑i=1n(yi−axi−b)2=∑i=1n2(yi−axi−b)(−xi)=2∑i=1n(−xiyi+axi2+bxi)∵∂a∂L=0∴∑i=1n(−xiyi+axi2+bxi)=0⇒−n(σxy−y^x^)+an(σx2+x^2)+bnx^=0⇒−(σxy+y^x^)+a(σx2+x^2)+bx^=0\begin{align*} \frac{\partial}{\partial a} &= \sum_{i=1}^{n}(y_i - ax_i - b)^2 \\ &= \sum_{i=1}^{n} 2(y_i -ax_i - b)(-x_i) \\ &= 2\sum_{i=1}^{n} (-x_iy_i + ax_i^2 + bx_i) \\ &\because \frac{\partial a}{\partial L} = 0 \\ &\therefore \sum_{i=1}^{n} (-x_iy_i + ax_i^2 + bx_i) = 0\\ &\Rightarrow -n(\sigma_{xy} -\hat{y}\hat{x}) + an(\sigma_x^2 + \hat{x}^2) + bn\hat{x} = 0 \\ &\Rightarrow -(\sigma_{xy} +\hat{y}\hat{x}) + a(\sigma_x^2 + \hat{x}^2) + b\hat{x} = 0 \end{align*} ∂∂b=∑i=1n(yi−axi−b)2=∑i=1n−2(yi−axi−b)=−2∑i=1n(yi−axi−b)∵∂b∂L=0∴∑i=1n(yi−axi−b)=0⇒−ny^+anx^+bn=0⇒−y^+ax^+b=0\begin{align*} \frac{\partial}{\partial b} &= \sum_{i=1}^{n}(y_i - ax_i - b)^2 \\ &= \sum_{i=1}^{n} -2(y_i -ax_i - b) \\ &= -2\sum_{i=1}^{n} (y_i -ax_i - b) \\ &\because \frac{\partial b}{\partial L} = 0 \\ &\therefore \sum_{i=1}^{n} (y_i -ax_i - b) = 0\\ &\Rightarrow -n\hat{y} + an\hat{x} + bn = 0 \\ &\Rightarrow -\hat{y} + a\hat{x} + b = 0 \\ \end{align*} {a(σx2+x^2)+bx^−(σxy+y^x^)=0ax^+b−y^=0⇒b=y^−ax^⇒aσx2+ax^2+y^x^−ax^2−σxy−y^x^=0⇒a=σxyσx2(regression coefficient)⇒b=y^−σxyσx2x^\begin{align*} &\begin{cases} &a(\sigma_x^2 + \hat{x}^2) + b\hat{x} -(\sigma_{xy}+\hat{y}\hat{x}) = 0 \\ &a\hat{x} + b -\hat{y} = 0 \\ \end{cases} \\ &\Rightarrow b = \hat{y} - a\hat{x} \\ &\Rightarrow a\sigma_x^2 + \cancel{a\hat{x}^2} + \cancel{\hat{y}\hat{x}} - \cancel{a\hat{x}^2} -\sigma_{xy} - \cancel{\hat{y}\hat{x}} = 0 \\ &\Rightarrow a = \frac{\sigma_{xy}}{\sigma^2_x} \quad \text{(regression coefficient)} \\ &\Rightarrow b = \hat{y} - \frac{\sigma_{xy}}{\sigma^2_x} \hat{x} \\ \end{align*} ∵a=σxyσx2b=y^−σxyσx2x^∴y=ax+b⇒y=σxyσx2x+y^−σxyσx2x^⇒y−y^=σxyσx2(x−x^)⇒y−y^=σxyσxσy⋅σyσx(x−x^)⇒y−y^=ρxy⋅σyσx(x−x^)\begin{align*} &\because a = \frac{\sigma_{xy}}{\sigma^2_x} \quad\quad b = \hat{y} - \frac{\sigma_{xy}}{\sigma^2_x} \hat{x} \\ &\therefore y = ax + b \\ &\Rightarrow y = \frac{\sigma_{xy}}{\sigma^2_x}x + \hat{y} - \frac{\sigma_{xy}}{\sigma^2_x} \hat{x} \\ &\Rightarrow y - \hat{y} = \frac{\sigma_{xy}}{\sigma^2_x}(x - \hat{x}) \\ &\Rightarrow y - \hat{y} = \frac{\sigma_{xy}}{\sigma_x\sigma_y} \cdot \frac{\sigma_{y}}{\sigma_x}(x - \hat{x}) \\ &\Rightarrow y - \hat{y} = \rho_{xy} \cdot \frac{\sigma_{y}}{\sigma_x}(x - \hat{x}) \end{align*}
  • Closed-form solution (Normal Equation):
w∗=(X⊤X)−1X⊤yw^* = (X^\top X)^{-1} X^\top y

where XX is the design matrix.

Note

DESIGN MATRIX

X=[1x11x12⋯x1d1x21x22⋯x2d⋮⋮⋮⋱⋮1xn1xn2⋯xnd]X = \begin{bmatrix} 1 & x_{11} & x_{12} & \cdots & x_{1d} \\ 1 & x_{21} & x_{22} & \cdots & x_{2d} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n1} & x_{n2} & \cdots & x_{nd} \end{bmatrix}
  • Rows correspond to observations (data points).
  • Columns correspond to features (including the constant 1 for intercept).

∙\bullet Linear regression with non-linear relationships

  • Polynomial Regression
  • Replace xx with some non-linear functions
p(u∣x,θ)=N(y∣w⊺ϕ(x),σ2)p(u \mid x, \theta) = N(y \mid w^\intercal \phi(x), \sigma^2)
  • Basis function expansion
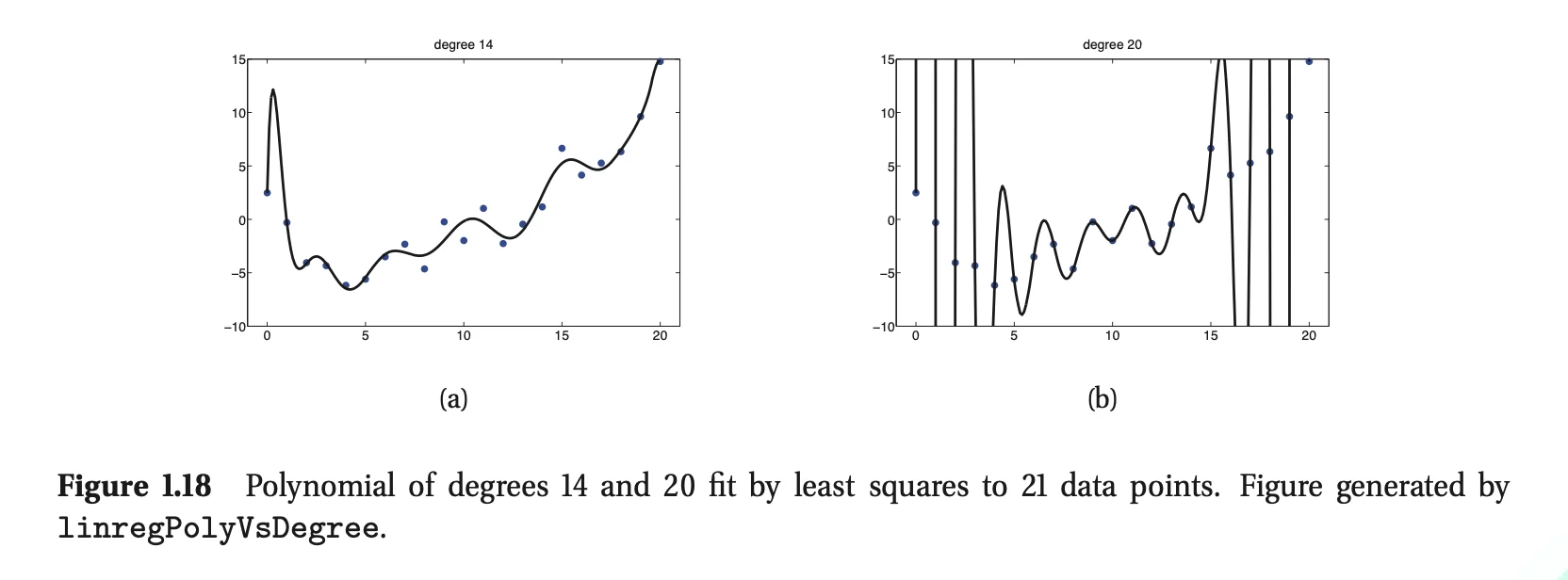
  • e.g. ϕ(x)=[1,x,x2,…,xd]\phi(x) = [1, x, x^2, \ldots, x^d], for d=14d = 14 and d=20d = 20

clipboard.png

Logistic Regression

  • Generalize Linear Regression to the binary classification

1. Replace Gaussian Distribution to Bernoulli Distribution

p(y∣x,w)=Ber(y∣μ(x))p(y \mid x, w) = Ber(y\mid \mu(x)) \\
  • y∈{−1,1}y\in \{-1, 1\}
  • μ(x)=E[y∣x]=p(y=1∣x)\mu(x) = \mathbb{E}[y \mid x] = p(y = 1 \mid x)

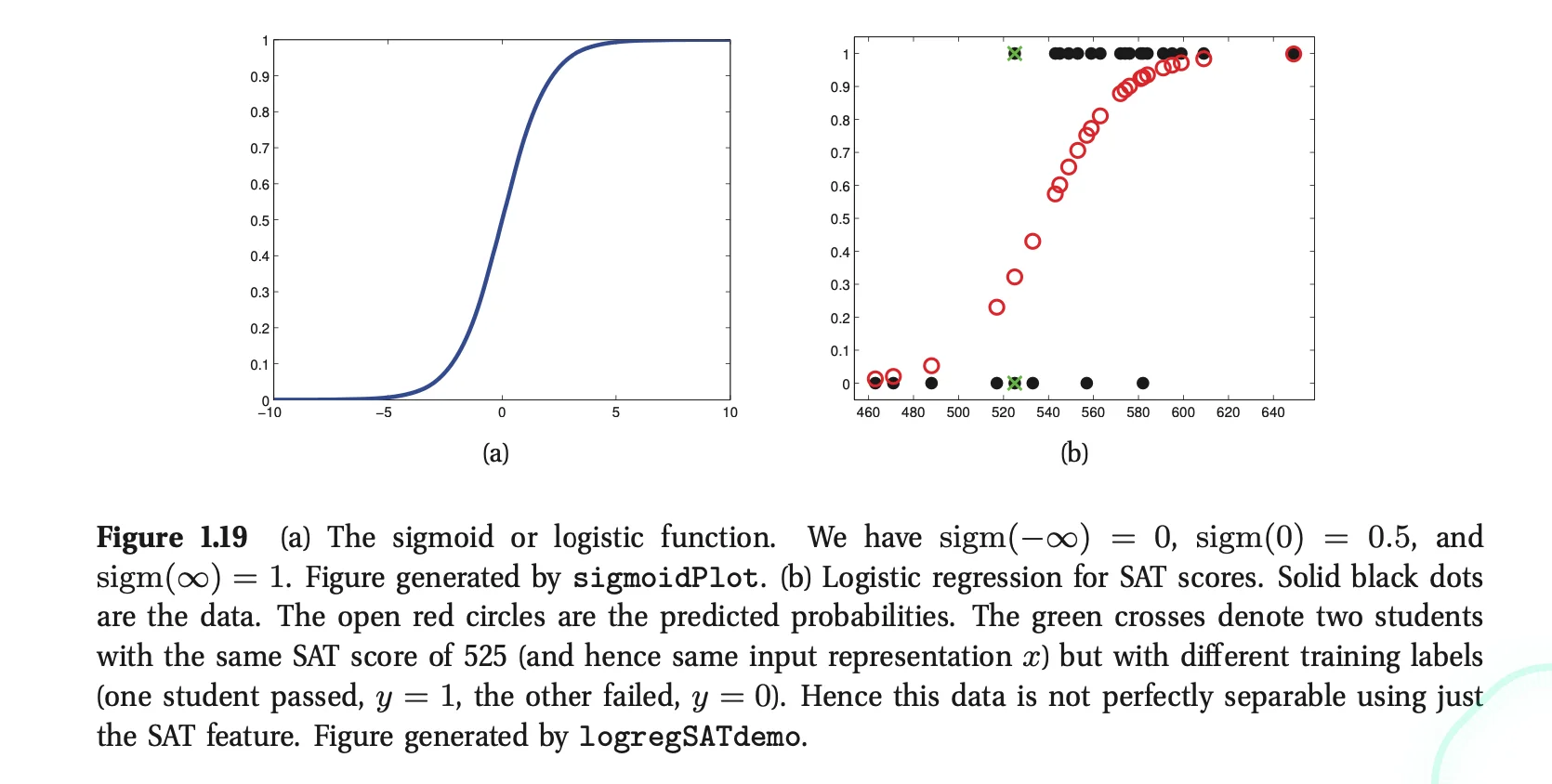
2. Pass μ(x)\mu(x) through sigmoid function

sigm(η)≜11+e−η=eηeη+1sigm(\eta) \triangleq \frac{1}{1 + e^{-\eta}} = \frac{e^\eta}{e^\eta + 1} μ(x)=sigm(w⊺x)\mu(x) = sigm(w^\intercal x)
  • The squashing function sigmoid maps the whole real line to [0,1][0, 1]
p(x∣x,w)=Ber(y∣sigm(w⊺x))p(x \mid x, w) = Ber(y \mid sigm(w^\intercal x))

3. Example: p(yi=1∣xi,w)=sigm(w0+w1xi)p(y_i = 1 \mid x_i, w) = sigm(w_0 + w_1 x_i)

clipboard.png

Model Selection

  • We can decide on which model to select based on the misclassification rate
err(f,D)=1N∑i=1NI(f(xi)≠yi)⋅where I(f(xi)≠yi)={1(f(xi)≠yi)0(f(xi)=yi)\begin{align*} &err(f, D) = \frac{1}{N}\sum_{i=1}^N \mathbb{I}(f(x_i) \ne y_i) \\ &\cdot where\ \mathbb{I}(f(x_i) \ne y_i) = \begin{cases} &1 \quad(f(x_i) \ne y_i) \\ &0 \quad(f(x_i) = y_i) \end{cases} \end{align*}
  • Example of an increased error rate due to the increase in K. (over-smoothing)

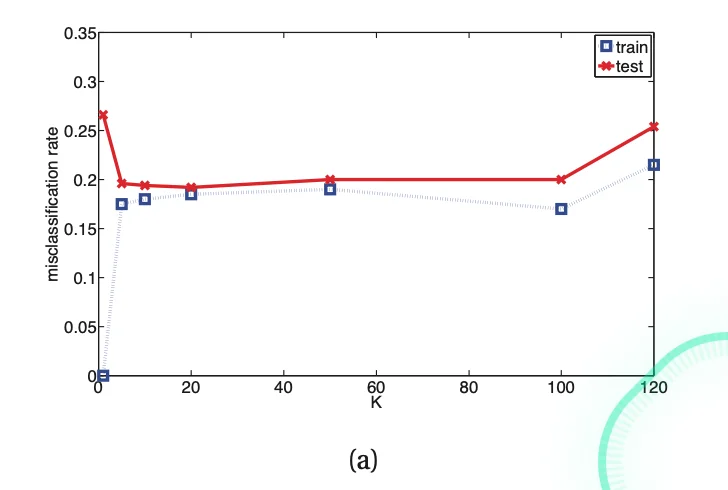
clipboard.png

  • For complex models (small KK), the method overfits
  • For simple models (large KK), the method underfits

Validation

  • Create a test set by partitioning data into different parts
  • usually 80%80\% for training and 20%20\% for testing

∙\bullet Cross Validation

  • Split data into KK folds. For each fold k∈{1,…,K}k \in \{1, \ldots, K\}, we train on all data but the kthk^{th} fold.
  • We test our trained model on the kthk^{th} fold.
  • Leave-one out cross validation (LOOCV)
  • set K=NK = N, leaving 1 test case for validation