1. Introduction and KNN

What is ML?

Definition

  • A computer program is said to
  • learn from experience E
  • with respect to some class of tasks T
  • and performance measure P
  • IF its performance at tasks in T, as measured by P, improves with E.

Note

Design algorithms that:

  • improves their performance
  • on some task
  • with experience (training data)

Categories

Supervised Learning

  • Given labeled data, find a function taht goes from that data to label.
  • Given x∈Xx \in X, predict y∈Yy \in Y construct a prediction rule
h:X→Yh: X \rightarrow Y

Discrete Labels

  • Binary classification: 2 categories
  • Multi-class classification: more than 2 categories

Continuous Labels

  • Regression: Analyze the relationship between dependent variables and independent variables

Unsupervised Learning

  • Given x∈Xx \in X, learn h(X)h(X)
  • learning without a teacher
  • e.g. clustering and PCA

Good ML Algorithm

  • SHOULD: Generalize well on test data
  • SHOULD NOT: Overfit the training data

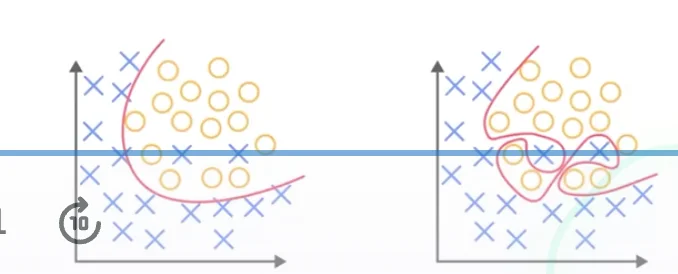
clipboard.png

KNN

  • similar points are likely to have the same labels
  • Dataset: D{(x(i),y(i))}i=1ND\{(x^{(i)}, y^{(i)})\}^N_{i=1}
  • New Datapoint: xx
  • Prediction: h(x)h(x)

Screenshot 2025-08-29 at 12.43.37

Algorithm

  1. Find the top KK nearest, under metric dd
  2. Return the most common label among these KK neighbors
  • For regession, the average value of the neighbors is returned

How to measure closeness?

  • Rely on a distance metric.

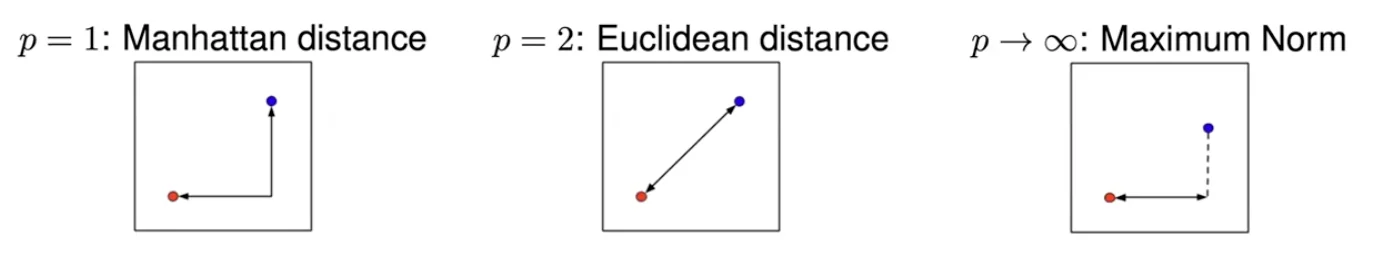
Minkowski Distance

  • the common metric
  • ∀x,z∈Rd\forall x, z \in \R^d
d(x,z)=(∑r=1d∣xr−zr∣p)1/pd(x, z) = (\sum^d_{r=1}\mid x_r - z_r \mid^p)^{1/p}
  • For each dimension, calculate the distance between rthr^{th} x and rthr^{th} z
  • d: distance
  • Special cases

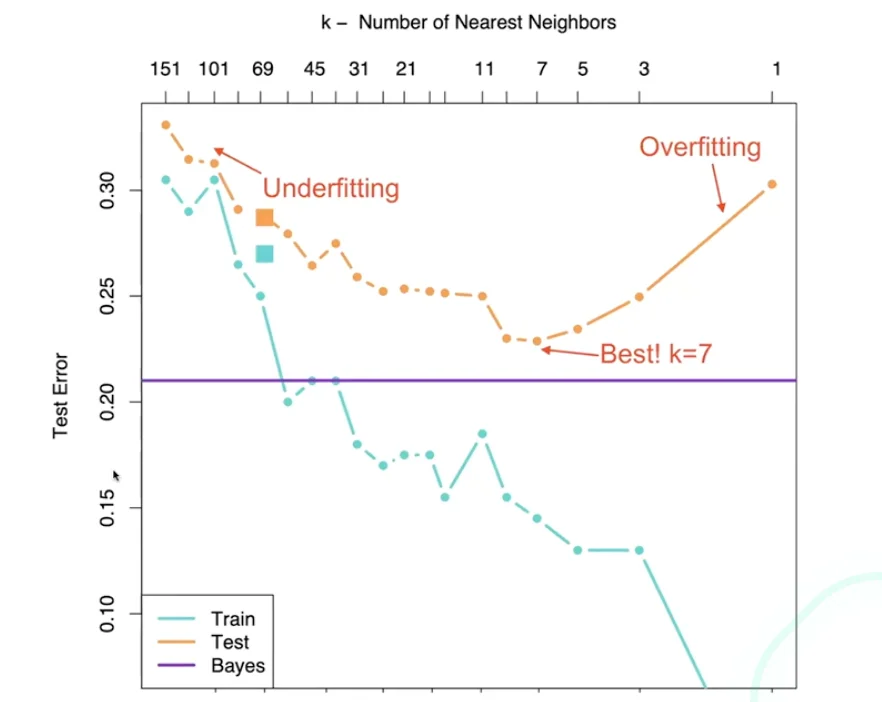
clipboard.png clipboard.png

The choice of K

  • Small K -> label has noise
  • Large K -> The boundary becomes smoother

Caution

Very large K may make the algorithm to include examples that are really far off.

What’s the best K

clipboard.png

Issues

  • Memory issue
  • sensitive to outliers and easily fooled by irrelevant attributes
  • 0 training time; computationally expensive O(Nd)
  • If d is large -> curse of dimensionality

Hyperparameters

  • We DO NOT CHOOSE hyperparameters to minimize training or testing errors

Solution

  • randomly take out 10~50% of training and use it instead of the test set to estimate test error.
  • Validation Set: the set taking out to verify the test set.

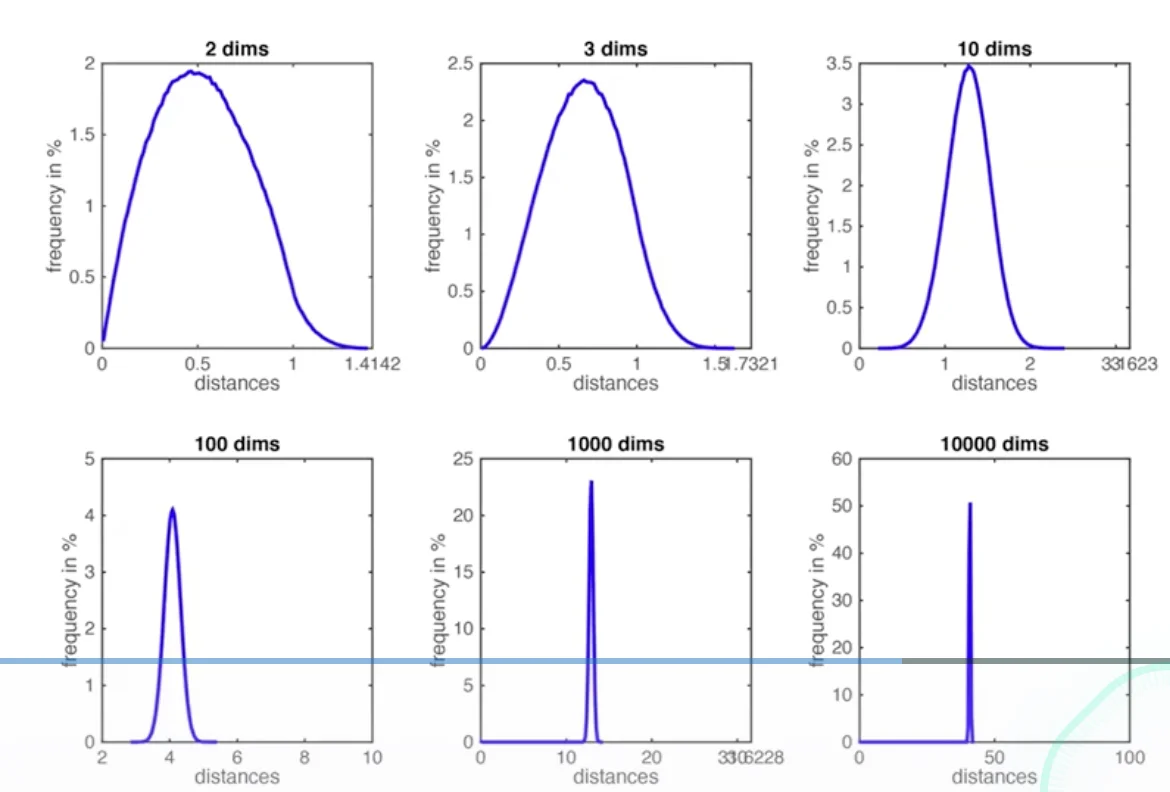
Curse of Dimensionality

clipboard.png

  • Assume data lives in [0,1]d[0, 1]^d, and all training data is sampled uniformly. And we observe the neighbors fall inside the small cube
  • The probability of sampling a point inside the small cube is roughly KN\frac{K}{N}
ld=KNl≈(KN)1d\begin{align*} &l^d = \frac{K}{N} \\ &l \approx (\frac{K}{N})^{\frac{1}{d}} \end{align*}

  • NN: The total number of data that we sample

  • KK: nearest neighbors fall inside the small cube.

  • If K=10K = 10 and N=1000N = 1000, how big is ll

  • d = 2, l = 0.1

  • d = 10, l = 0.63

  • d = 100, l = 0.955

  • d = 1000, l = 0.9954

Caution

When dd is large, the KK nearest neighbors will be almost all over the place

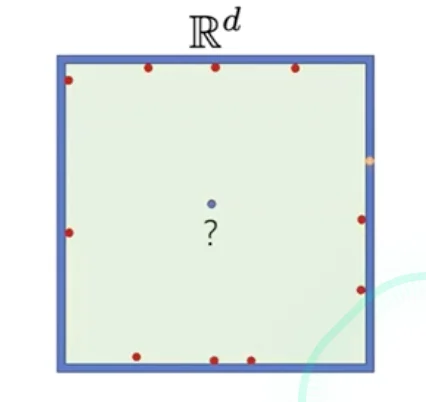
clipboard.png

  • In high dimensional space, you don’t have neighbors anymore

clipboard.png

Data may have low dimensional structure

  • High dimensional space may contain low dimensional subspaces
  • Your data may lie in a low dimensional subspace or its low dimensional

KNN vs. Linear Classifier

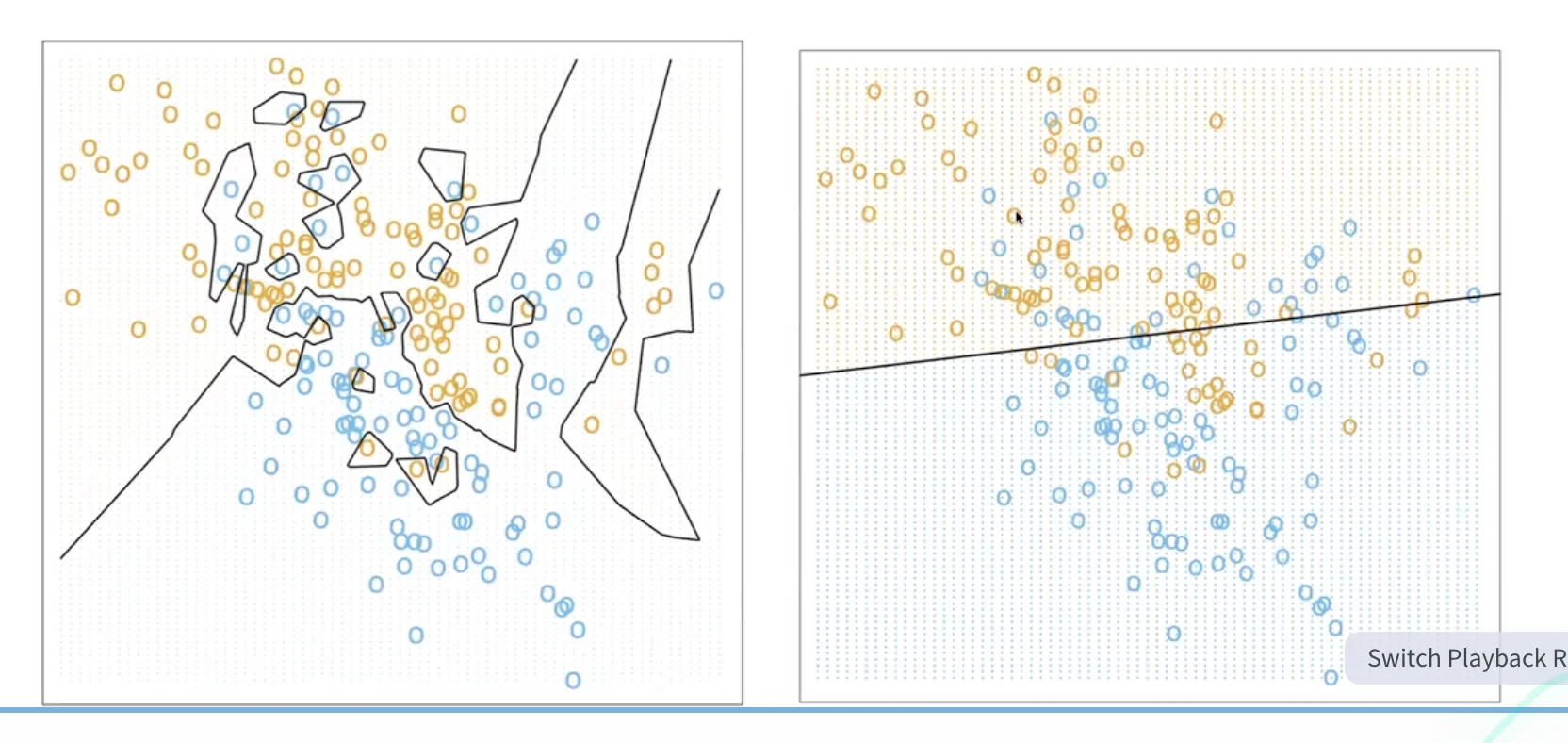
clipboard.png

KNN Summary

  • KNN is simple and effective if the distance reflects dissimilarity
  • works when data is low-dimensional
  • DOES NOT work for high-dimensional data due to sparsity.