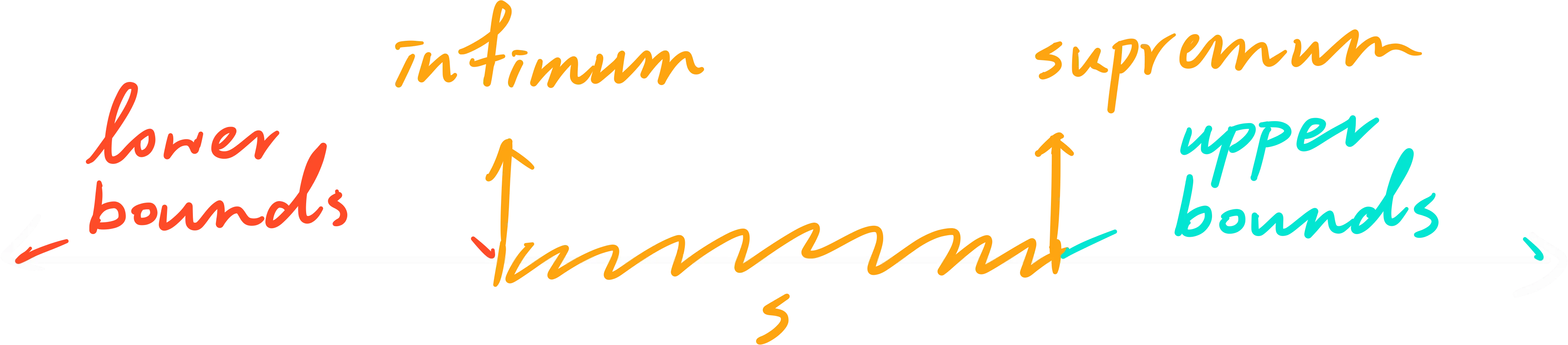2. Perceptron

Linear Separability

  • A set of examples is linearly separable if there exists a linear decision boundary that can separate the points

Perceptron

clipboard.png

  • Perceptron is a linear classifier that only converges when data is linearly separable.
  • Dataset:
  • D={x(i),y(i)}NiD = \{{x^{(i)}, y^{(i)}}\}^{i}_{N}
  • Assumptions:
  • Binary classification: y∈{−1,+1}y \in \{-1, +1\}
  • Data is linearly separable

Note

The only hyperparameter in the perceptron is the max number of iterations

  • Too many iterations may lead to overfit
  • Too few iterations may lead to underfit

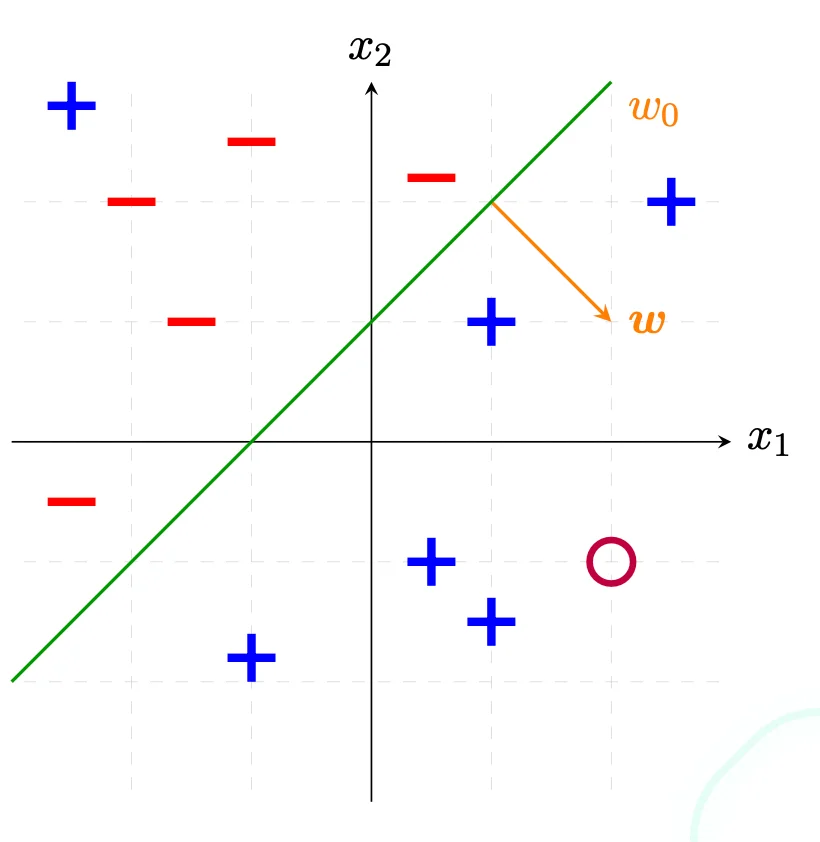
Hyperplane

H={x:w⊺x+w0=0}⇒w⋅x=0\begin{align*} H &= \{x: w^\intercal x + w_0 = 0\} \\ &\Rightarrow w \cdot x = 0 \end{align*}
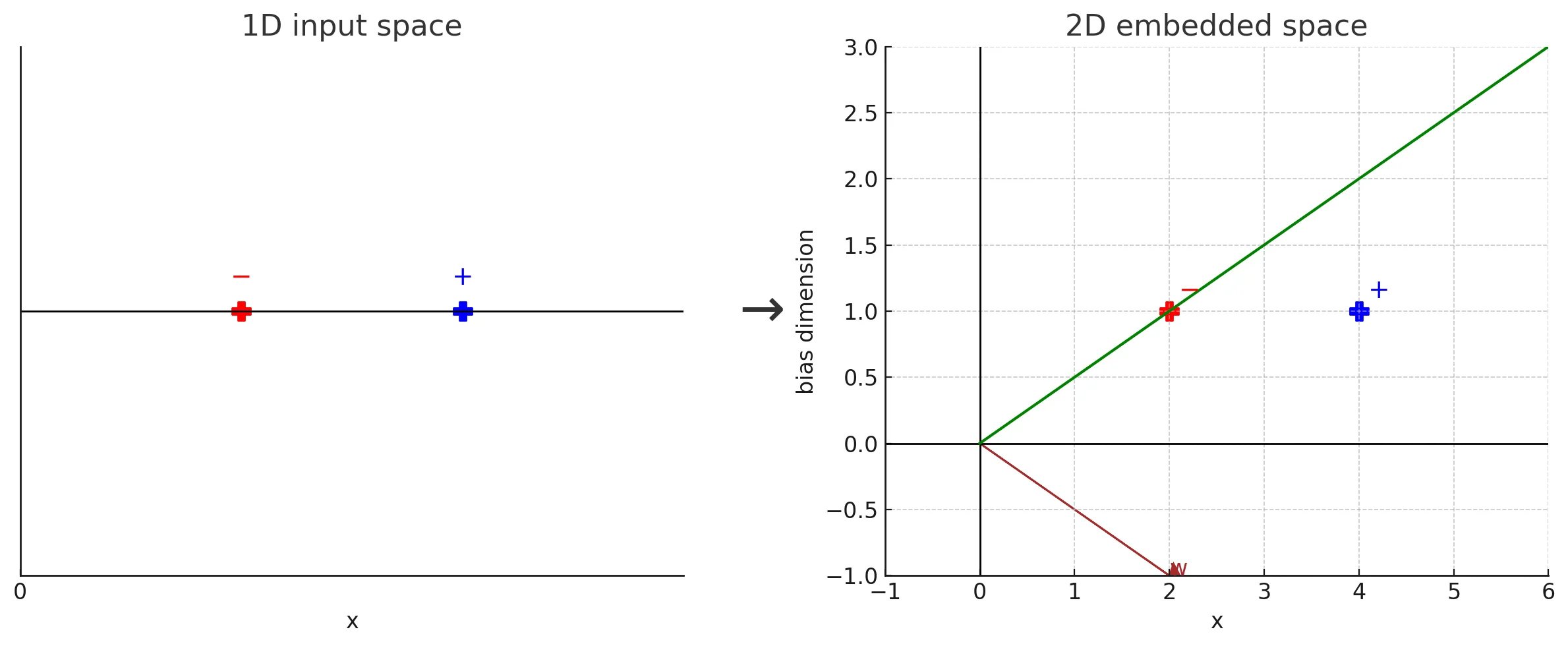
  • The bias term w0w_0 is needed to have a non-zero threshold that allows the activation value to be increased by some fixed value b.

Positive Example

w⊺x+w0>0w^\intercal x + w_0 > 0

Negative Example

w⊺x+w0<0w^\intercal x + w_0 < 0

Classifier

h(x)=sign(w⊺x+w0)h(x) = sign(w^\intercal x + w_0)

Updating w

  • What the perceptron does.
w←w+y(i)x(i)w \leftarrow w + y^{(i)}x^{(i)}

Important

Why is ww perpendicular to the hyperplane

  • w⋅x=0w \cdot x = 0 means that all points of xx lies on the hyperplane
  • As w⋅x=0w \cdot x = 0 implies perpendicularity, ww and the hyperplane are perpendicular
  • Example clipboard.png

Notational Hack

w⊺x+w0⇒w⊺xw^\intercal x + w_0 \Rightarrow w^\intercal x
  • As we rewrite the notations as follows:

x = \begin{bmatrix} x_1 \ \vdots \ x_d \end{bmatrix} \Rightarrow \begin{bmatrix} \uparrow \ x \ \downarrow \ 1 \end{bmatrix}

2. $$ w = \begin{bmatrix} w_1 \\ \vdots \\ w_d \end{bmatrix} \Rightarrow \begin{bmatrix} \uparrow \\ w \\ \downarrow \\ w_0 \end{bmatrix}
  • The result of this rewrite (increment dimensionality by 1)

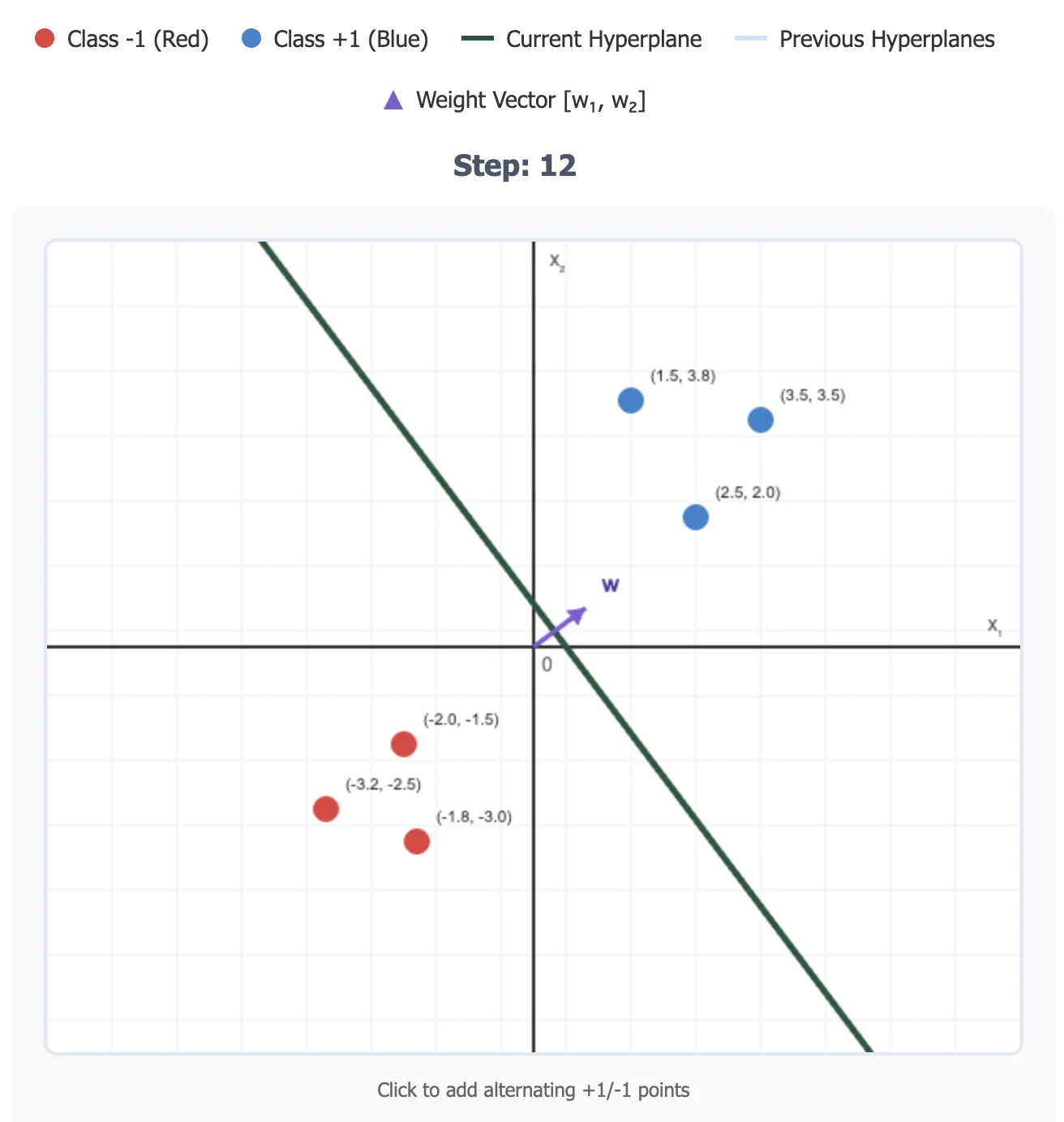
clipboard.png

Perceptron Algorithm

Algorithm

PerceptronTrain(D,MaxIter)1:wd←0, for all d=1…D// initialize weights2:b←0// initialize bias3:for iter=1…MaxIter do4:for all (x,y)∈D do5:a←∑d=1Dwdxd+b// compute activation for this example6:if ya≤0 then7:wd←wd+yxd, for all d=1…D// update weights8:b←b+y// update bias9:end if10:end for11:end for12:return w0,w1,…,wD,b\begin{array}{l} \hline {\text{PerceptronTrain}}(D, MaxIter) \\ \hline \begin{array}{ll} 1: & w_d \leftarrow 0, \text{ for all } d = 1 \ldots D & \text{// initialize weights} \\ 2: & b \leftarrow 0 & \text{// initialize bias} \\ 3: & \textbf{for } iter = 1 \ldots MaxIter \textbf{ do} \\ 4: & \quad \textbf{for all } (x,y) \in D \textbf{ do} \\ 5: & \quad \quad a \leftarrow \sum_{d=1}^D w_d x_d + b & \text{// compute activation for this example} \\ 6: & \quad \quad \textbf{if } ya \leq 0 \textbf{ then} \\ 7: & \quad \quad \quad w_d \leftarrow w_d + y x_d, \text{ for all } d = 1 \ldots D & \text{// update weights} \\ 8: & \quad \quad \quad b \leftarrow b + y & \text{// update bias} \\ 9: & \quad \quad \textbf{end if} \\ 10: & \quad \textbf{end for} \\ 11: & \textbf{end for} \\ 12: & \textbf{return } w_0, w_1, \ldots, w_D, b \\ \end{array} \\ \hline \end{array}

Python

def perceptron(D: DataSet, w: WeightVector):
 # init
 w = [0, 0... 0].T
 while True:
 # indicate whether w is changed
 changed = False
 for i in range(N):
 # at init step or misclassified
 if y[i] * (w @ x[i]) <= 0:
 w = w + y[i] * x[i] # update the weight vector
 changed = True
 if not changed:
 break

Why y(i)(w⊺x(i))≤0y^{(i)}(w^\intercal x^{(i)}) \le 0?

clipboard.png

Note

y∈{1,−1}y \in \{1, -1\}, which is a scalar not a vector

  • Error-driven Updating: Only update the weights if a prediction is wrong
  • If the updated w wneww_{new} leads to the correct classification of the input
y(wnew⊺x)=y((w+yx)⊺x)=y(w⊺x+yx⊺x)=y(w⊺x)+yyx⊺x=y(w⊺x)+∣∣x∣∣2>y(w⊺x)\begin{align*} &y(w_{new}^\intercal x ) \\ &= y((w + yx)^\intercal x) \\ &= y(w^\intercal x + yx^\intercal x) \\ &= y(w^\intercal x) + yyx^\intercal x \\ &= y(w^\intercal x) + ||x||^2 \\ &> y(w^\intercal x) \end{align*}
  • (w⊺x(i))(w^\intercal x^{(i)})
  • w⋅x(i)>0w\cdot x^{(i)}> 0
  • The input vector points to the same general direction as the weight vector
  • w⋅x(i)<0w \cdot x^{(i)} < 0
  • The input vector points to the opposite direction to the weight vector
  • w⋅x=0w \cdot x = 0
  • The input vector is perpendicular to the weight vectorx
  • y(i)y^{(i)}
  • The true label
  • y(i)×w⋅x>0  ⟺  sign(y)=sign(w⋅x)y^{(i)} \times w \cdot x > 0 \iff sign(y) = sign(w \cdot x)
  • y(i)×w⋅x≤0  ⟺  sign(y)≠sign(w⋅x)y^{(i)} \times w \cdot x \le 0 \iff sign(y) \ne sign(w \cdot x)

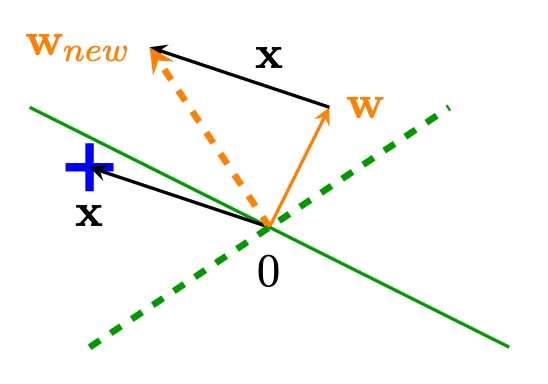
What does a perceptron update do?

  • Given y∈{1,−1}y \in \{1, -1\}
w←w+y(i)x(i)←w±x(i)\begin{align*} w &\leftarrow w + y^{(i)}x^{(i)} \\ &\leftarrow w \pm x^{(i)} \end{align*}

Note

  • Update of ww: is increased by y(i)x(i)y^{(i)}x^{(i)}
  • Bias is updated by y(i)y^{(i)}

Mistake on positive sample (y=1y = 1 and w⊺x≤0w^\intercal x \le 0)

  • Increase the new weight wneww_{new}, so that it’s greater than the original one
wnew⊺x=(w+x)⊺x=w⊺x+x⊺x>w⊺x\begin{align*} w^\intercal_{new} x &= (w + x)^\intercal x \\ &= w^\intercal x + x^\intercal x \\ &> w^\intercal x \end{align*}

Mistake on negative sample (y=−1y = -1 and w⊺x≥0w^\intercal x \ge 0)

  • Decrease the new weight wneww_{new}, so that it’s greater than the original one
wnew⊺x=(w−x)⊺x=w⊺x−x⊺x<w⊺x\begin{align*} w_{new}^\intercal x &= (w - x)^\intercal x \\ &= w^\intercal x - x^\intercal x \\ &< w^\intercal x \end{align*}

How often can a perceptron misclassify a point x repeatedly

  • Assume KK updates have been done
y(w+kyx)⊺x≤0⇒y(w⊺x)+k∣∣x∣∣2≤0⇒k∣∣x∣∣2≤−y(w⊺x)⇒k≤−y(w⊺x)/∣∣x∣∣2\begin{align*} &y(w + kyx)^\intercal x \le 0 \\ &\Rightarrow y(w^\intercal x) + k ||x||^2 \le 0 \\ &\Rightarrow k ||x||^2 \le -y(w^\intercal x) \\ &\Rightarrow k \le -y(w^\intercal x) / ||x||^2 \end{align*}

Perceptron Performance

  • ∃w∗\exist w^* such that
y(i)(w∗⊺)x(i)>0,∀(x(i)),y(i)∈Dy^{(i)}(w^{*\intercal})x^{(i)} > 0, \forall (x^{(i)}), y{(i)} \in D
  • Rescale w∗w^* and each data point such that
∙∣∣w∗∣∣=1∙∣∣x(i)∣∣≤1,∀x(i)∈D\begin{align*} &\bullet ||w^*|| = 1 \\ &\bullet ||x^{(i)}|| \le 1, \forall x^{(i)} \in D \end{align*}
  • Margin of a hyperplane γ\gamma is defined as:
min⁡∣w∗Tx(i)∣,∀x(i)∈D\min|w^{*T}x^{(i)}|, \forall x^{(i)} \in D
  • Formal Definition:
  • Margin
γ=margin(D,w)={min⁡(x,y)∈Dy(w⋅x)if w separates D−∞otherwise\gamma = margin(\mathbf{D}, w) = \begin{cases} \min_{(x,y) \in \mathbf{D}} y(w \cdot x) & \text{if } w \text{ separates } \mathbf{D} \\ -\infty & \text{otherwise} \end{cases}
  • Margin of a data set
  • The margin of dataset D is the supremum (maximum) over all possible weight vectors w of the margin function.”
  • In this case maximum and supremum only differ when margin(D,w)margin(\mathbf{D}, w) produces −∞-\infty clipboard.png
γD=sup⁡w,b{margin(D,w)}\gamma_D = \sup_{w, b}\{margin(\mathbf{D, w)}\}

Important

If all the conditions above hold, the perceptron algorithm makes at most

1γ2\frac{1}{\gamma^2}

updates.

Proof

  • Given that:
  • yw⊺x≤0yw^\intercal x \le 0 holds if xx is misclassified by ww
  • yw∗⊺x>0yw^{*\intercal} x > 0 holds as w∗w^* leads to a separating hyperplane for the correct classification.

∙\bullet Effect of an update on w⊺w∗:w^\intercal w^*:

  • For each update, w⊺w∗w^\intercal w^* grows at least by γ\gamma
wnew⊺w∗=(w+yx)⊺w∗=w⊺w∗+yw∗⊺x∵sign(y)=sign(w∗⊺x)∵yw∗Tx=∣w∗⊺x∣≥γ≥w⊺w∗+γ(∵yw∗⊺x≥γ)\begin{align*} w_{new}^\intercal w^* &= (w + yx)^\intercal w^* \\ &= w^{\intercal}w^* + yw^{*\intercal}x \\ &\because sign(y) = sign(w^{*\intercal} x) \\ &\because yw^{*T}x = |w^{*\intercal}x| \ge \gamma \\ &\ge w^\intercal w^* + \gamma \quad (\because yw^{*\intercal}x \ge \gamma) \end{align*}

∙\bullet Effect of an update on w⊺w:w^{\intercal}w:

  • For each update, w⊺ww^\intercal w grows at most 11
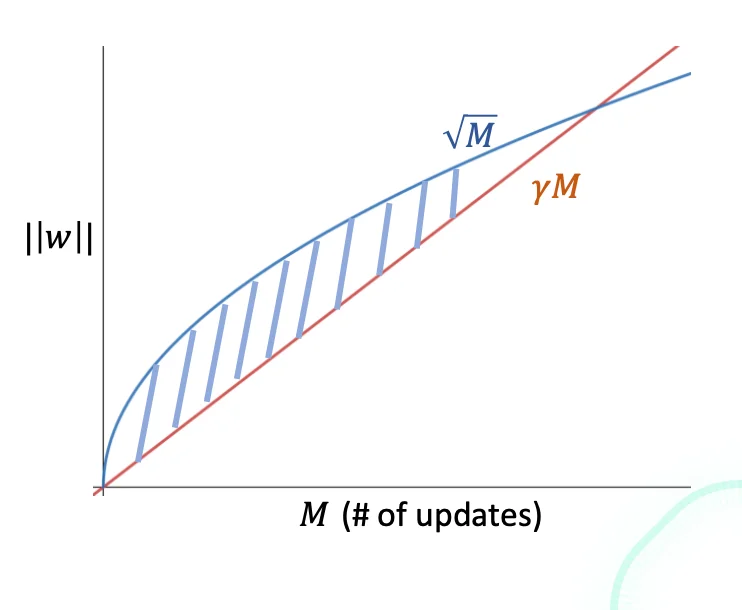
wnew⊺wnew=(w+yx)⊺(w+yx)=w⊺w+2yw⊺x+y2x⊺x≤w⊺w+1(∵ywTx≤0, x⊺x≤1)\begin{align*} w_{new}^\intercal w_{new} &= (w + yx)^\intercal (w + yx)\\ &= w^\intercal w + 2yw^\intercal x + y^2x^\intercal x \\ &\le w^\intercal w + 1 \quad (\because yw^Tx \le 0,\ x^\intercal x \le 1) \end{align*}

∙\bullet Suppose we have M updates

Mγ≤wTw∗=∣wTw∗∣≤∣∣w∣∣⋅∣∣w∗∣∣(Cauchy-Schwarz Inequality)=∣∣w∣∣⋅1(since ∣∣w∗∣∣=1)=∣∣w∣∣=w⊺w≤M(by the effect of an update on w⊺w)⇒Mγ≤M⇒M2γ2≤M⇒M≤1γ2\begin{align*} M\gamma &\leq w^T w^* \\ &= |w^T w^*| \\ &\leq ||w|| \cdot ||w^*|| \quad \text{(Cauchy-Schwarz Inequality)} \\ &= ||w|| \cdot 1 \quad \text{(since } ||w^*|| = 1\text{)} \\ &= ||w|| \\ &= \sqrt{w^\intercal w} \\ &\le \sqrt{M} \quad \text{(by the effect of an update on } w^\intercal w) \\ &\Rightarrow M\gamma \le \sqrt{M} \\ &\Rightarrow M^2\gamma^2 \le M \\ &\Rightarrow M \le \frac{1}{\gamma^2} \end{align*}

clipboard.png

Improved Generalization: Voting and Averaging

Caution

The key issue of the initial perceptron is that it counts later points more than it counts earlier points.

Tip

Give more say to weight vectors that survive long enough

Voted Perceptron

  • Each weight vector has its own counter for survival times
  • w(1), …, w(k)w^{(1)},\ \dots,\ w^{(k)}: K+1K + 1 weight vectors with bias w0w_0 included
  • c(1), …, c(k)c^{(1)},\ \dots,\ c^{(k)}: survival times for each vector
y^=sign(∑k=1Kc(k)×sign(w(k)⋅x^))\hat{y} = sign(\sum_{k=1}^{K} c^{(k)} \times sign(w^{(k)} \cdot \hat{x}))

Averaged Perceptron

  • At test time, you predict according to the average weight vector rather than the voting.
y^=sign(∑k=1Kc(k)×(w(k)⋅x^))=sign(∑k=1Kc(k)×(w(k))⋅x^)\begin{align*} \hat{y} &= sign(\sum_{k=1}^{K} c^{(k)} \times (w^{(k)} \cdot \hat{x})) \\ &= sign(\sum_{k=1}^{K} c^{(k)} \times (w^{(k)}) \cdot \hat{x}) \\ \end{align*}

Algorithm

AveragedPerceptronTrain(D,MaxIter)1:wd←⟨0⃗, …, 0⃗⟩// initialize weights2:u⟨0⃗, …, 0⃗⟩// initialize cached weights3:for iter=1…MaxIter do4:for all (x,y)∈D do5:if y(w⋅x)≤0⃗ then6:w←w+yx5:u←u+ycx9:end if9:c←c+110:end for11:end for12:return w−1cu\begin{array}{l} \hline {\text{AveragedPerceptronTrain}}(D, MaxIter) \\ \hline \begin{array}{ll} 1: & w_d \leftarrow \langle\vec{\scriptstyle 0},\ \dots,\ \vec{\scriptstyle 0}\rangle& \text{// initialize weights} \\ 2: & u \langle \vec{\scriptstyle 0},\ \dots,\ \vec{\scriptstyle 0}\rangle& \text{// initialize cached weights} \\ 3: & \textbf{for } iter = 1 \ldots MaxIter \textbf{ do} \\ 4: & \quad \textbf{for all } (x,y) \in D \textbf{ do} \\ 5: & \quad \textbf{if } y(w \cdot x) \le \vec{\scriptstyle 0}\ then\\ 6: & \quad \quad w \leftarrow w + yx \\ 5: & \quad \quad u \leftarrow u + ycx \\ 9: & \quad \quad \textbf{end if} \\ 9: & \quad c \leftarrow c + 1 \\ 10: & \quad \textbf{end for} \\ 11: & \textbf{end for} \\ 12: & \textbf{return } w - \frac{1}{c} u \\ \\ \end{array} \\ \hline \end{array}