4. Linear Regression

Regression

f:X→Yf: X \rightarrow Y
  • where YY is continuous

Approach

  • Choose parameterized form for P(Y∣X,w)P(Y \mid X, w)
  • Derive learning algorithm as MLE or MAP

Parameterized form for P(Y∣X,w)P(Y \mid X, w)

  • Y is some deterministic f(X)f(X), plus random noise
y=f(x)+ϵwhere ϵ∼N(0,σ2)y = f(x) + \epsilon \quad where \ \epsilon \sim \mathcal{N}(0, \sigma^2)
  • Therefore, Y is a r.v. that follows
p(y∣x)=N(f(x),σ2)p(y \mid x) = \mathcal{N}(f(x), \sigma^2)

Consider Linear Regression

f(x)=wTx+w0(w∈Rd,w0∈R)p(y∣x)=N(wTx+w0,σ2)\begin{align*} &f(x) = w^Tx + w_0 \quad (w \in \R^d, w_0 \in \R) \\ &p(y \mid x) = N(w^Tx + w_0, \sigma^2) \end{align*}
  • Let x=[x1],w=[ww0]x = \begin{bmatrix}x \\ 1\end{bmatrix}, w = \begin{bmatrix}w \\ w_0\end{bmatrix}
p(y∣x)=N(wTx,σ2)p(y \mid x) = N(w^Tx, \sigma^2)

MLE

Quardratic Form

  • First, expand the prediction function
p(y∣x,w)=N(wTx,σ2)=12πσ2e−(y−w⊺x)22σ2\begin{align*} p(y \mid x, w) &= N(w^Tx, \sigma^2) \\ &= \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(y - w^\intercal x)^2}{2\sigma^2}} \end{align*}
  • Then, calculate the ww that maximizes this function (w^MLE\hat{w}^{MLE})
w^MLE=arg max⁡w∏i=1N12πσ2e−(y(i)−w⊺x(i))22σ2=arg max⁡w∑i=1Nlog⁡12πσ2+log⁡e−(y(i)−w⊺x(i))22σ2=arg max⁡w∑i=1Nlog⁡12πσ2−(y(i)−w⊺x(i))22σ2(Remove irrelevant term and flip sign)=arg min⁡w∑i=1N(y(i)−w⊺x(i))22σ2=arg min⁡w∑i=1N(y(i)−w⊺x(i))2=arg min⁡w∑i=1N(y(i)−w⊺x(i))2(Take the average)=arg min⁡w∑i=1N(y(i)−w⊺x(i))2\begin{align*} \hat{w}^{MLE} &= \argmax_w \prod^N_{i = 1} \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-\frac{(y^{(i)} - w^\intercal x^{(i)})^2}{2\sigma^2}} \\ &= \argmax_w \sum^N_{i = 1} \log \frac{1}{\sqrt{2 \pi \sigma^2}} + \log e^{-\frac{(y^{(i)} - w^\intercal x^{(i)})^2}{2\sigma^2}} \\ &= \argmax_w \sum^N_{i = 1} \log \frac{1}{\sqrt{2 \pi \sigma^2}} -\frac{(y^{(i)} - w^\intercal x^{(i)})^2}{2\sigma^2} \quad (\text{Remove irrelevant term and flip sign})\\ &= \argmin_w \sum^N_{i = 1} \frac{(y^{(i)} - w^\intercal x^{(i)})^2}{2\sigma^2} \\ &= \argmin_w \sum^N_{i = 1} (y^{(i)} - w^\intercal x^{(i)})^2 \\ &= \argmin_w \sum^N_{i = 1} (y^{(i)} - w^\intercal x^{(i)})^2 \quad (\text{Take the average})\\ &= \argmin_w \sum^N_{i = 1} (y^{(i)} - w^\intercal x^{(i)})^2 \\ \end{align*}

Tip

Therefore, we derive that, the MLE is the minimization of the Ordinary Least Squares (OLS)

l(w)=1N∑i=1N(y(i)−w⊺x(i))2l(w) = \frac{1}{N}\sum^N_{i = 1} (y^{(i)} - w^\intercal x^{(i)})^2

Matrix Form

let y=[y(i)⋮y(N)],X=[x(i)⊺⋮x(N)⊺]y = \begin{bmatrix} y^{(i)} \\ \vdots \\y^{(N)}\end{bmatrix}, \quad X = \begin{bmatrix}x^{(i)\intercal} \\ \vdots \\ x^{(N)\intercal}\end{bmatrix}

w=arg min⁡wl(w)=arg min⁡w1N∑i=1N(y(i)−w⊺x(i))2=arg min⁡w(y−Xw)T(y−Xw)=arg min⁡w(y⊺y−(Xw)⊺y−y⊺Xw+w⊺X⊺Xw)=arg min⁡w(y⊺y−2y⊺Xw+(Xw)⊺Xw)∂l∂w=−2y⊺X+X⊺Xw+(Xw)⊺X=00=−2y⊺X+2X⊺XwX⊺y=X⊺Xw(X⊺X)−1X⊺y=w\begin{align*} w &= \argmin_w l(w) \\ &= \argmin_w \frac{1}{N} \sum^N_{i = 1} (y^{(i)} - w^\intercal x^{(i)})^2 \\ &= \argmin_w (y - Xw)^T(y - Xw) \\ &= \argmin_w (y^\intercal y - (Xw)^\intercal y - y^\intercal Xw + w^\intercal X^\intercal Xw) \\ &= \argmin_w (y^\intercal y - 2y^\intercal Xw + (Xw)^\intercal Xw) \\ \frac{\partial l}{\partial w}&= - 2y^\intercal X + X^\intercal Xw + (Xw)^\intercal X = 0 \\ 0 &= -2y^\intercal X + 2X^\intercal Xw \\ X^\intercal y &= X^\intercal Xw \\ (X^\intercal X)^{-1}X^\intercal y &= w \\ \end{align*}
  • Therefore, we derive that:
w=(X⊺X)−1X⊺yw = (X^\intercal X)^{-1}X^\intercal y

MAP

w^MAP=arg max⁡wP(w∣x(1),y(1),…,x(N),y(N))=arg max⁡wP(x(1),y(1),…,x(N),y(N)∣w)P(w)P(x(1),y(1),…,x(N),y(N))=arg max⁡wP(x(1),y(1),…,x(N),y(N)∣w)P(w)=arg max⁡wP(y(1),…,y(N)∣x(1),…,x(N),w)P(x(1),…,x(N)∣w)P(w)=arg max⁡w∏i=1N[P(y(i)∣x(i),w)]P(w)Assume 0-mean Gaussian prior 12πτ2e−w⊺w2τ2=arg max⁡w∑i=1Nlog⁡P(y(i)∣x(i),w)+log⁡P(w)=arg min⁡w12σ2∑i=1NP(w⊺x(i)−y(i))−w⊺w2τ2Let λ=σ2Nτ2 and remove 12=arg min⁡w1N∑i=1N(w⊺x(i)−y(i))2+λ∣∣w∣∣22\begin{align*} \hat{w}^{MAP} &= \argmax_w P(w \mid x^{(1)}, y^{(1)}, \dots, x^{(N)}, y^{(N)}) \\ &= \argmax_w \frac{P(x^{(1)}, y^{(1)}, \dots, x^{(N)}, y^{(N)} \mid w)P(w)}{P(x^{(1)}, y^{(1)}, \dots, x^{(N)}, y^{(N)})} \\ &= \argmax_w P(x^{(1)}, y^{(1)}, \dots, x^{(N)}, y^{(N)} \mid w)P(w) \\ &= \argmax_w P(y^{(1)}, \dots, y^{(N)} \mid x^{(1)}, \dots, x^{(N)}, w)P(x^{(1)}, \dots, x^{(N)} \mid w)P(w) \\ &= \argmax_w \prod^N_{i= 1} \left[ P(y^{(i)} \mid x^{(i)}, w) \right]P(w) \\ &\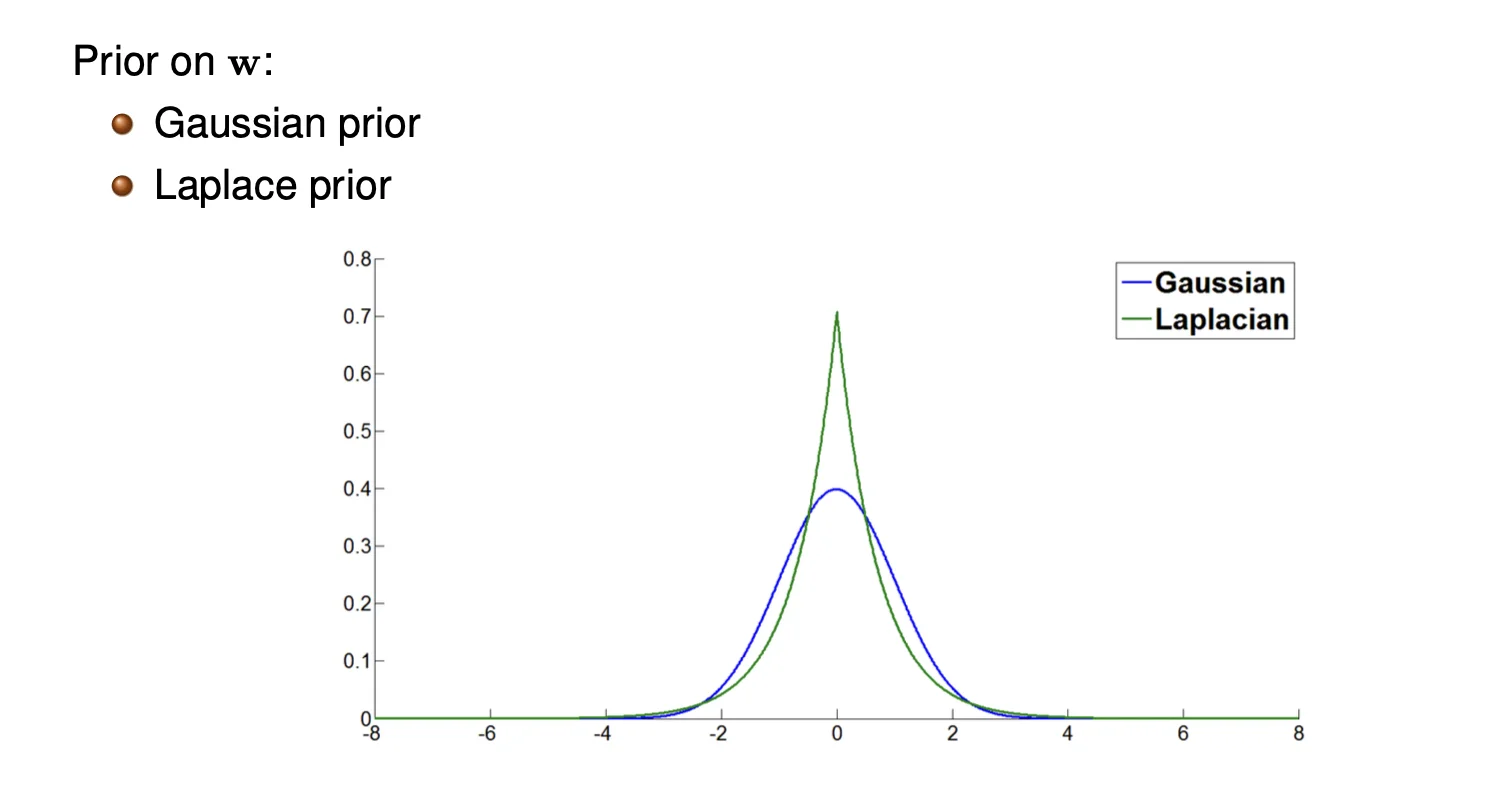text{Assume 0-mean Gaussian prior } \frac{1}{\sqrt{2 \pi \tau^2}}e^{-\frac{w^\intercal w}{2 \tau^2}}\\ &= \argmax_w \sum^N_{i=1} \log P(y^{(i)} \mid x^{(i)}, w) + \log P(w) \\ &= \argmin_w \frac{1}{2\sigma^2} \sum^N_{i=1} P(w^\intercal x^{(i)} - y^{(i)}) -\frac{w^\intercal w}{2 \tau^2} \\ &\text{Let }\lambda = \frac{\sigma^2}{N\tau^2} \text{ and remove } \frac{1}{2} \\ &= \argmin_w \frac{1}{N} \sum^N_{i = 1} (w^\intercal x^{(i)} - y^{(i)})^2 + \lambda ||w||_2^2 \end{align*}

Tip

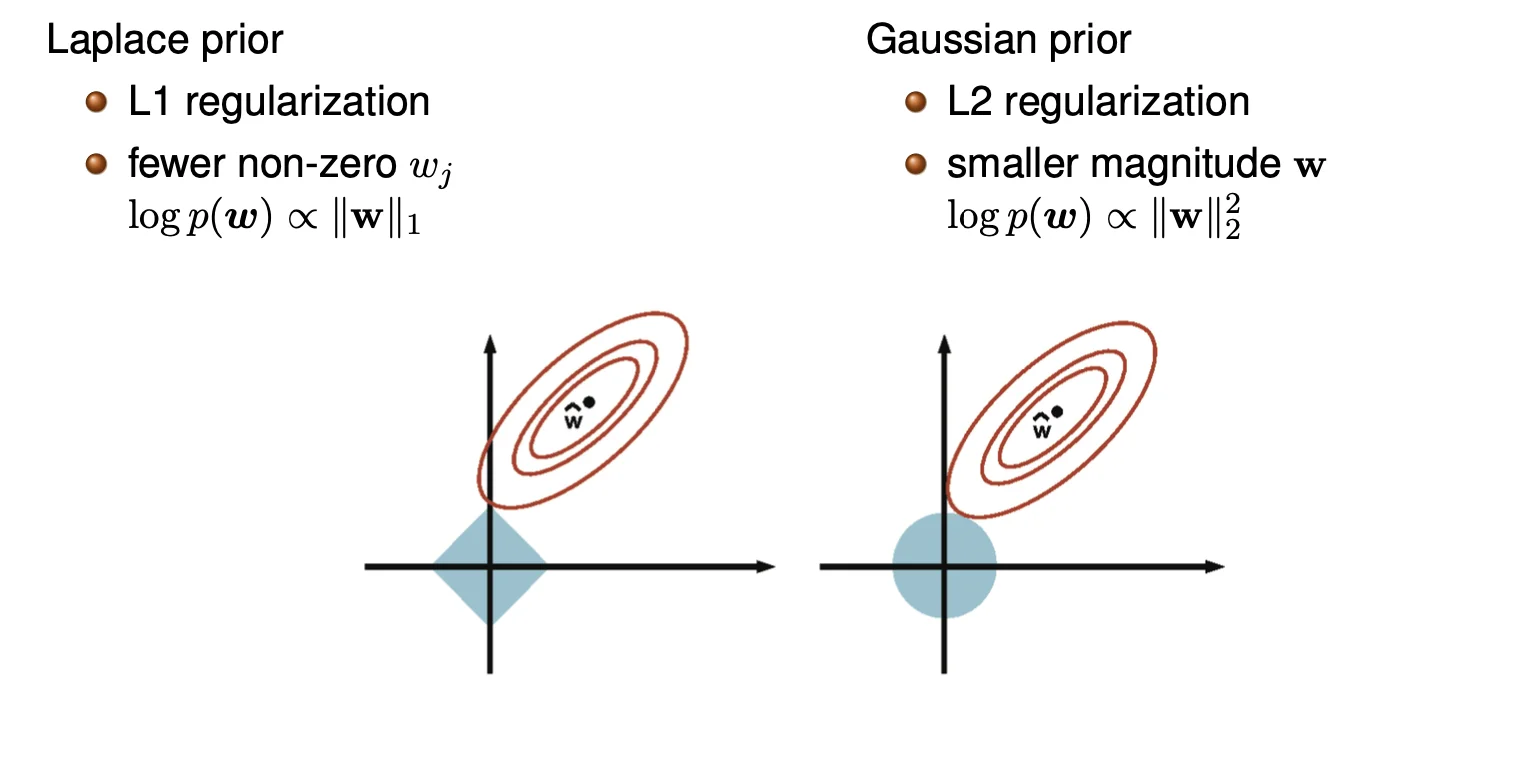
Therefore, with Gaussian prior equivalent to ridge regression (L2), we get closed-form solution:

w=(X⊺X+λI)−1X⊺yw = (X^\intercal X + \lambda I)^{-1} X^\intercal y

If Laplace Prior is assumed instead

Screenshot 2025-10-14 at 13.08.16

  • Assume Laplace prior for each wjw_j
wj:12be∣wj∣bw_j: \frac{1}{2b} e ^{\frac{|w_j|}{b}}
  • So we can redefine our prior as follows:
p(w)=1(2b)d+1e−1b∑i=1d∣wj∣log⁡p(w)∝∑i=1d∣wj∣=∣∣w∣∣1\begin{align*} &p(w) = \frac{1}{(2b)^{d + 1}} e^{-\frac{1}{b}\sum^{d}_{i = 1} |w_j|} \\ &\log p(w) \propto \sum^d_{i = 1} | w_j | = ||w||_1 \end{align*}
  • Finally, we can derive the wMAPw^{MAP} as:
wMAP=arg max⁡wlog⁡p(w)+∑i=1Nlog⁡p(y(i)∣x(i),w)=arg max⁡wc∣∣w∣∣1+∑i=1N(y(i)−w⊺x(i))2\begin{align*} w^{MAP} &= \argmax_w \log p(w) + \sum^N_{i = 1} \log p(y^{(i)} \mid x^{(i)}, w) \\ &= \argmax_w c ||w||_1 + \sum^N_{i=1} (y^{(i)} - w^\intercal x^{(i)})^2 \end{align*}

Screenshot 2025-10-14 at 19.22.38