9.1 Cross Validation and Model Selection

Example: Sine Target

  • Let’s say we have the following two models:
H0:h(x)=bH1:h(x)=ax+b\begin{align*} &H_0: h(x) = b \\ &H_1: h(x) = ax + b \end{align*}

Important

Which is better?

  • Main question →\rightarrow better for what?

Approximation

  • Let’s say we want to approximate the following function
f:[−1,1]→R    f(x)=sin(πx)f: [-1, 1] \rightarrow \R \;\; f(x) = sin(\pi x)

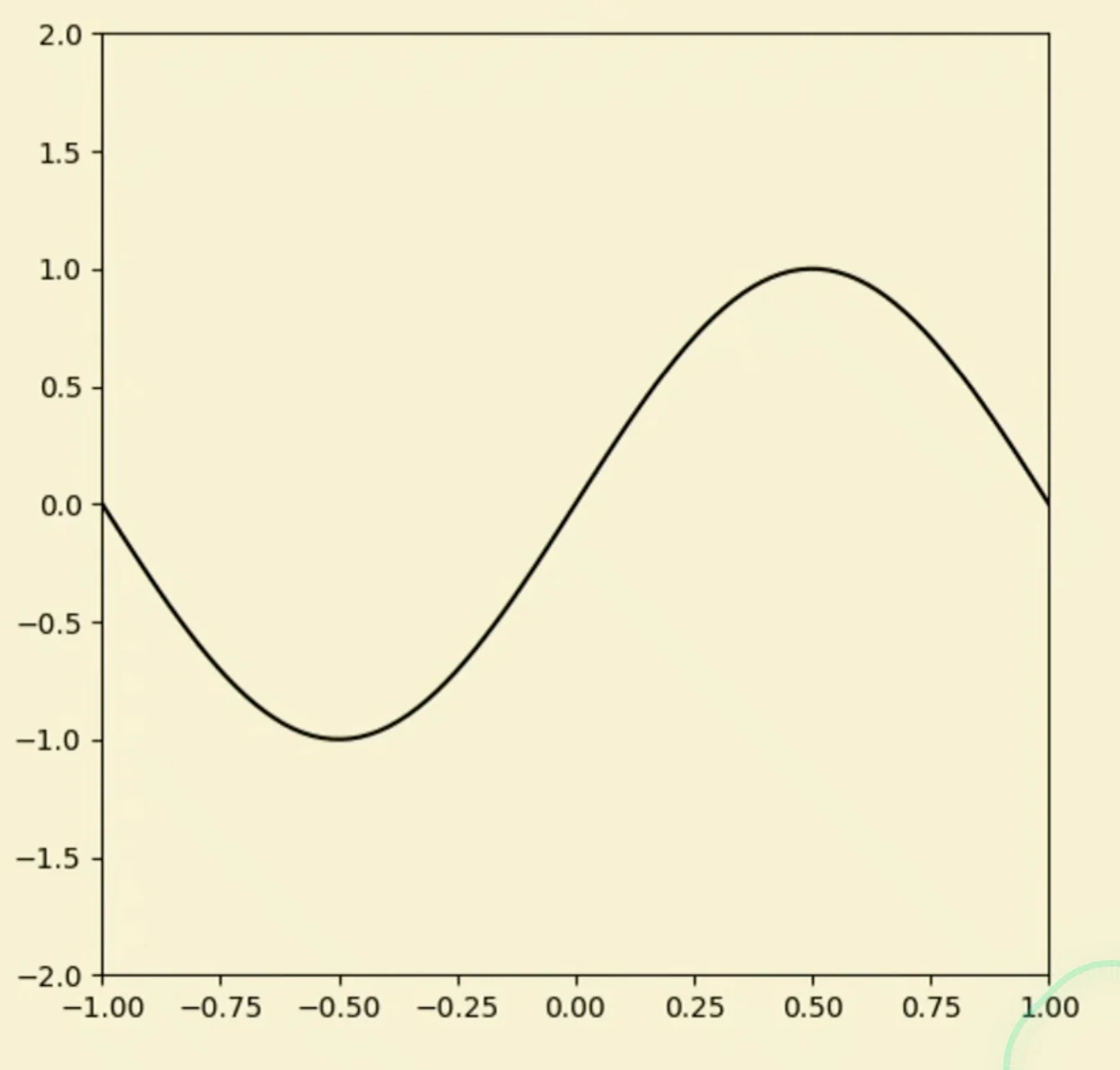
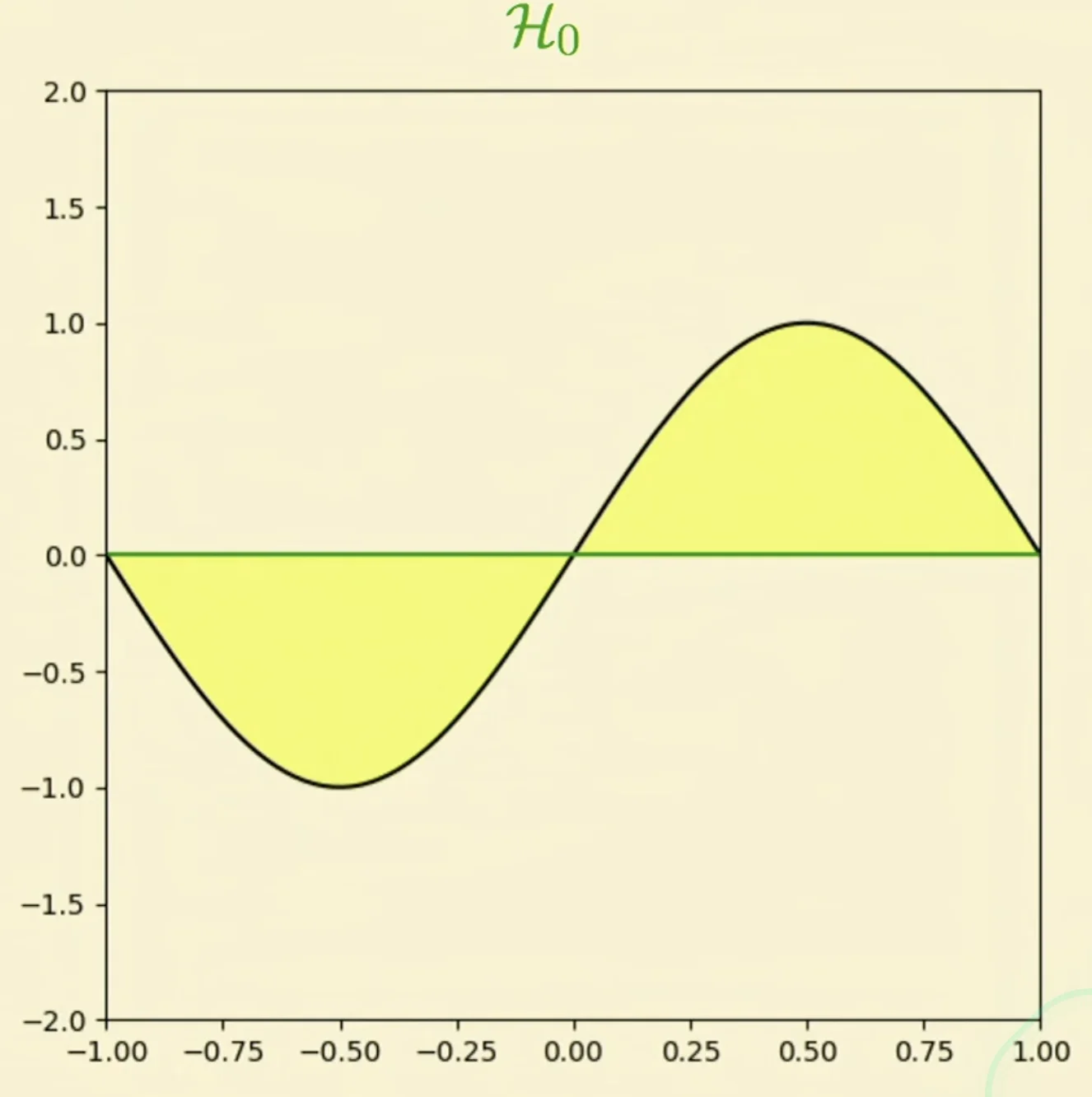
clipboard.png

∙\bullet Approximate with H1H_1

clipboard.png

  • the yellow part tells us how far we are from the sine function
  • Error=0.20Error = 0.20

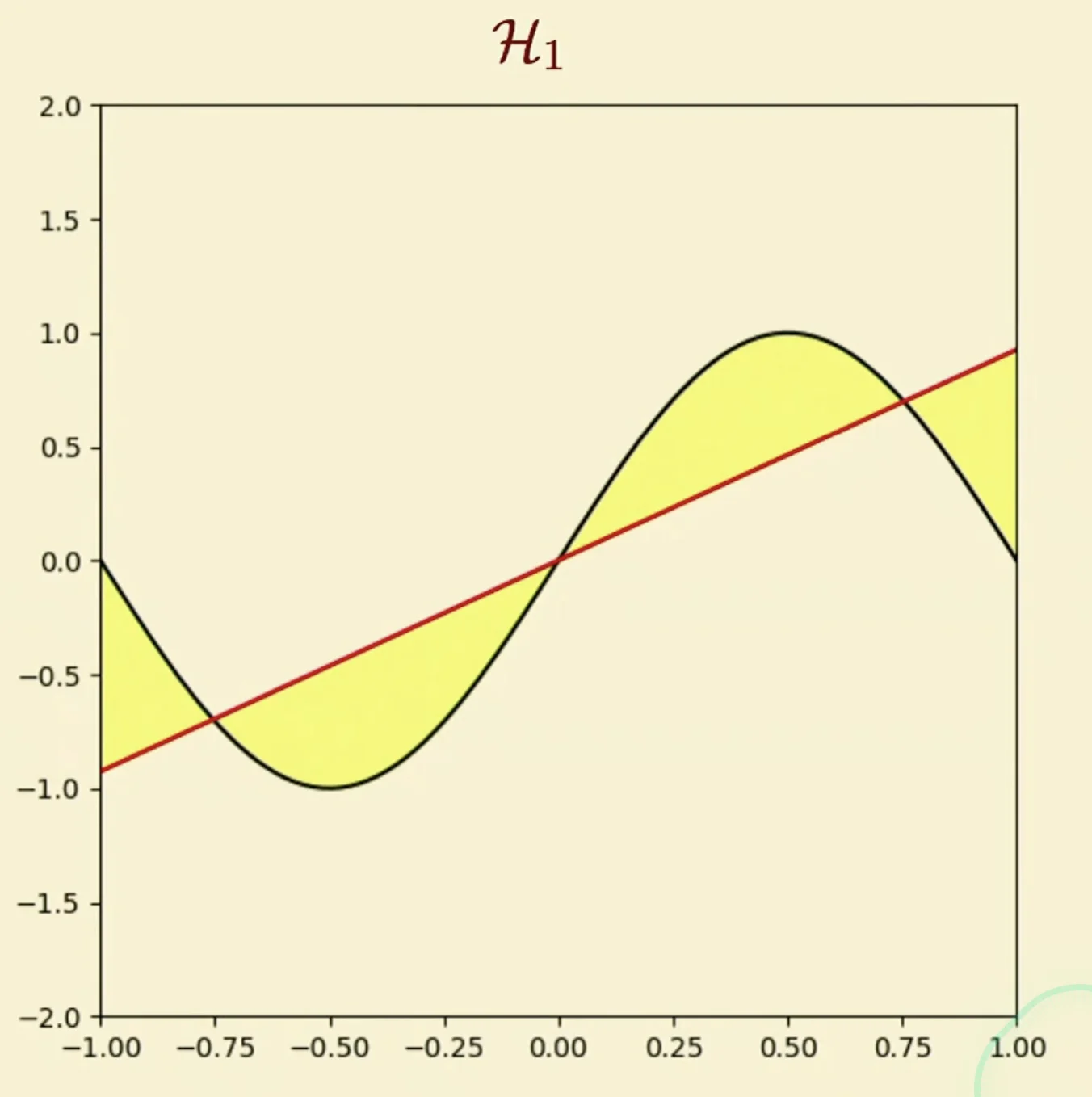
∙\bullet Approximate with H0H_0

clipboard.png

  • Error=0.50Error = 0.50

Tip

From the approximation perspective, the linear model wins.

Learning

  • For learning, we give our two models two data points and train them

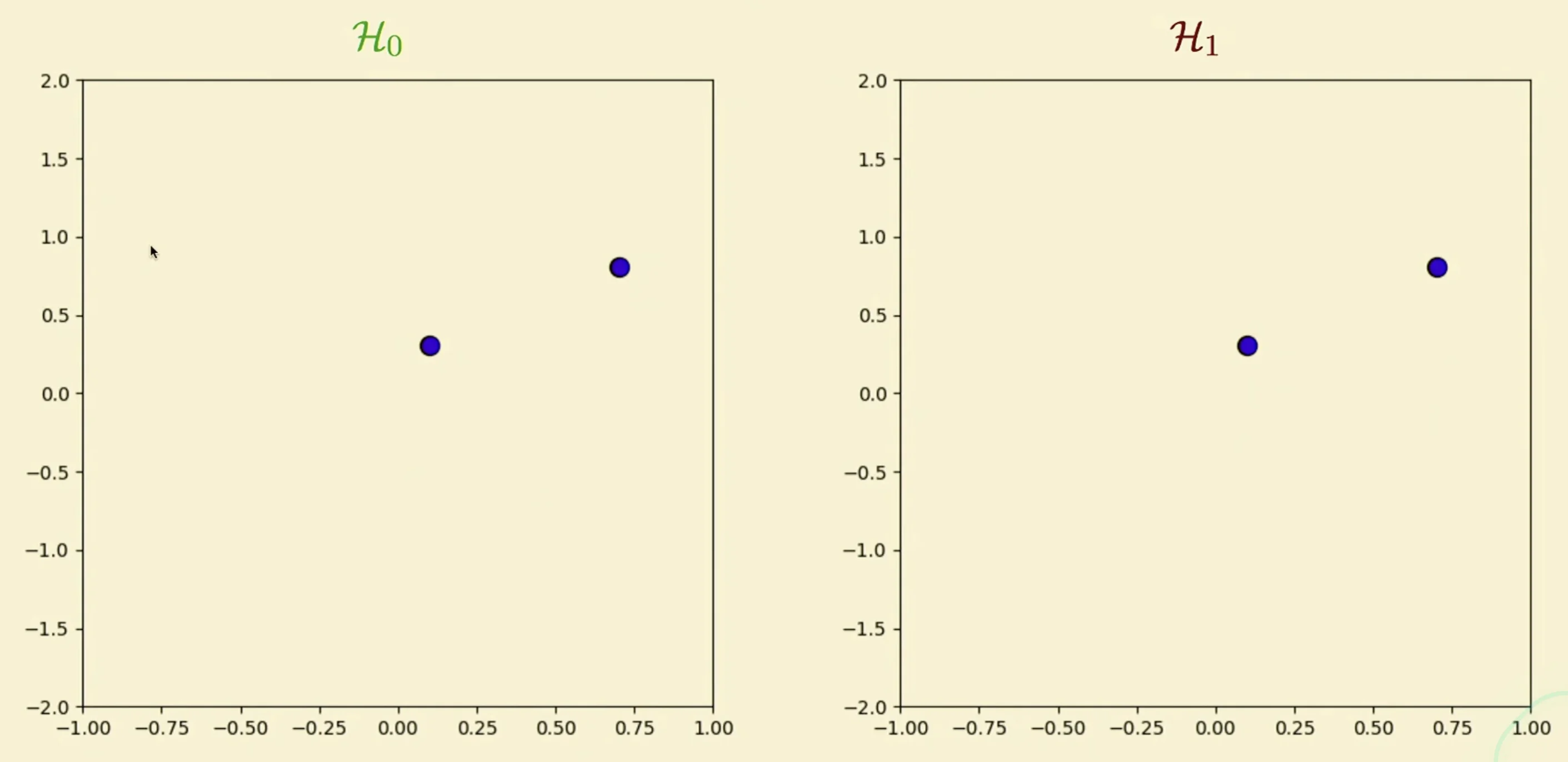
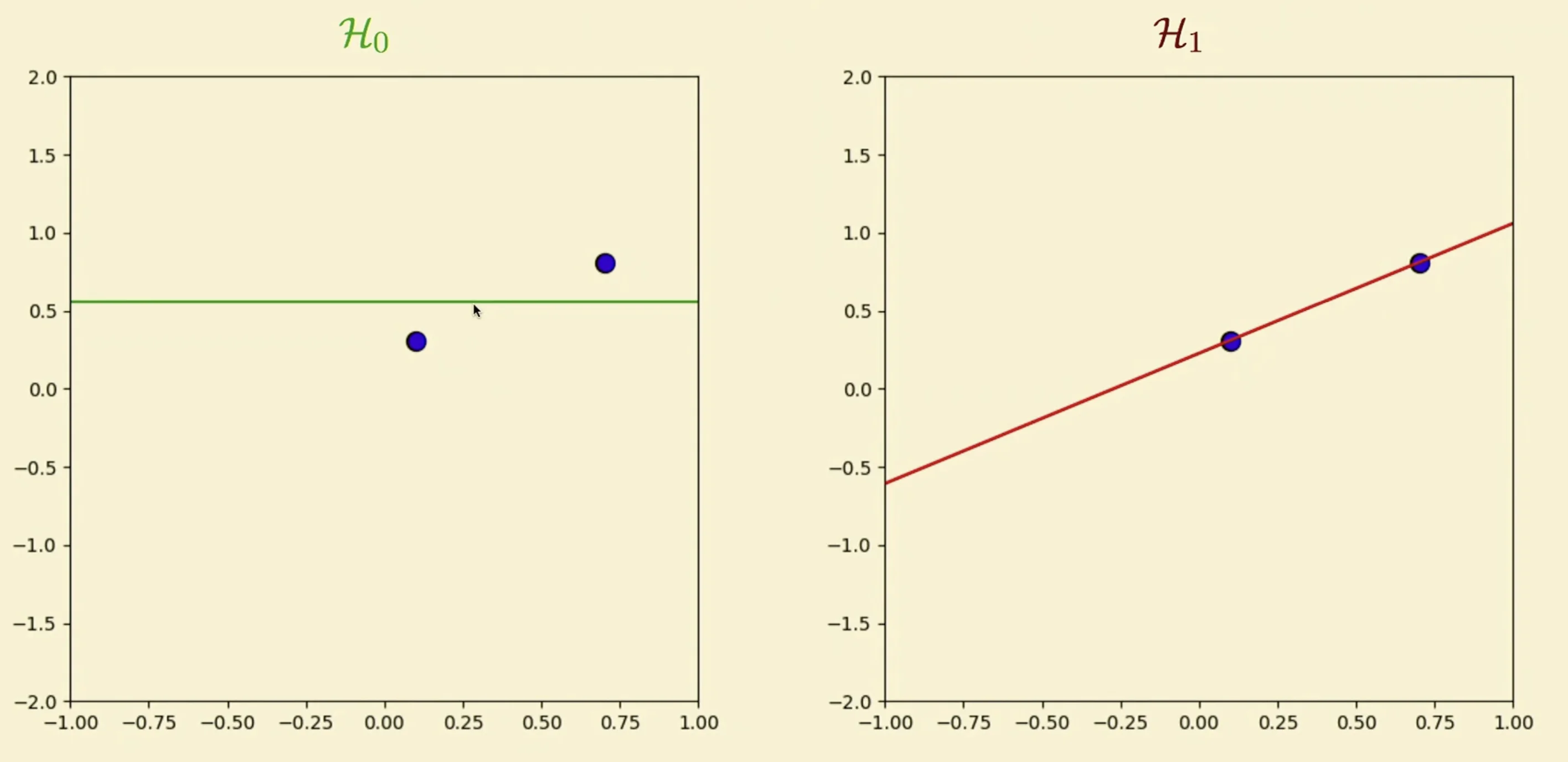
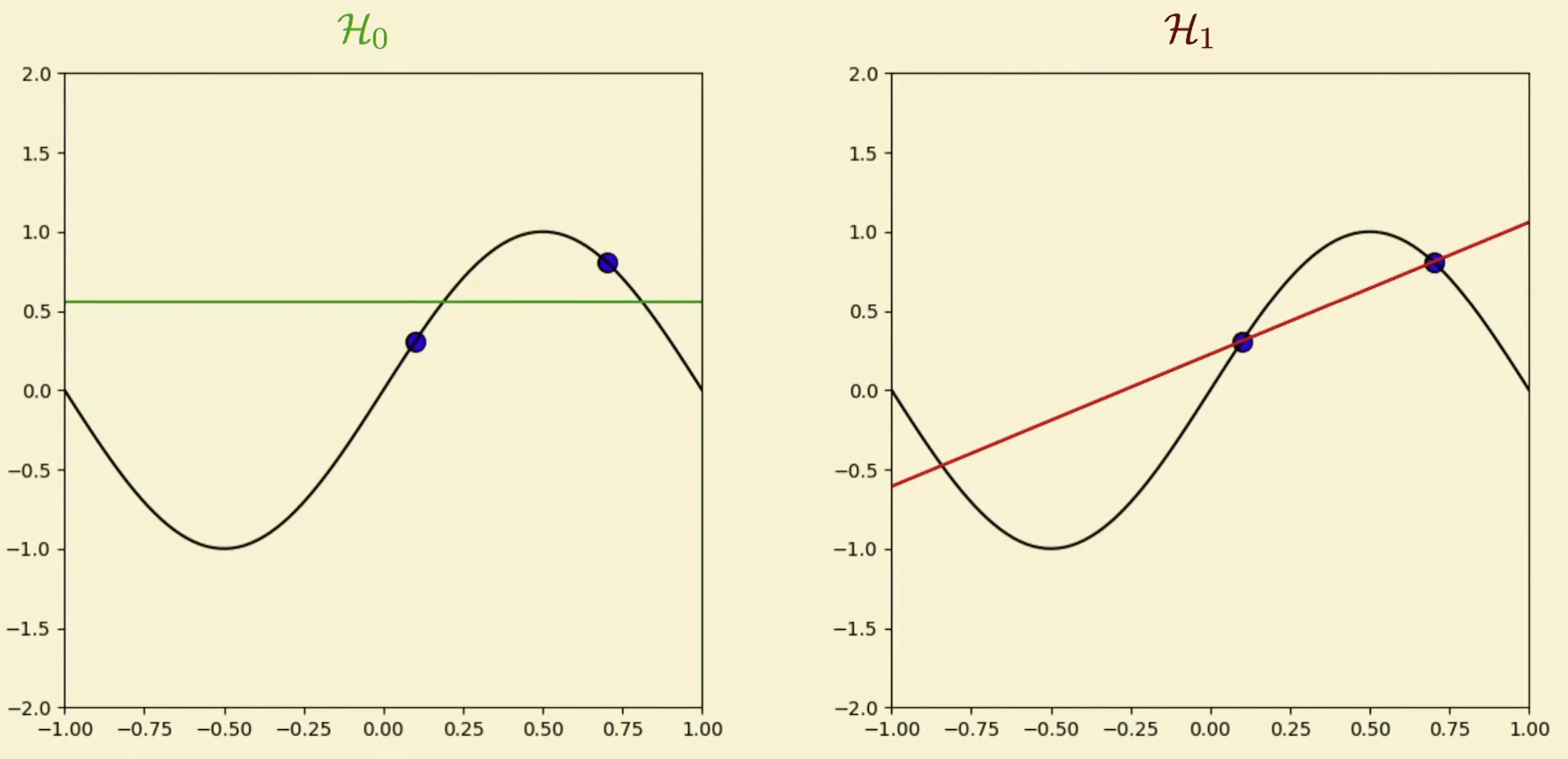
clipboard.png clipboard.png clipboard.png

  • Which one is better? We don’t know as it depends on what are the initial two data points given. Therefore, we need the bias variance method for us to determine which method produces less error.

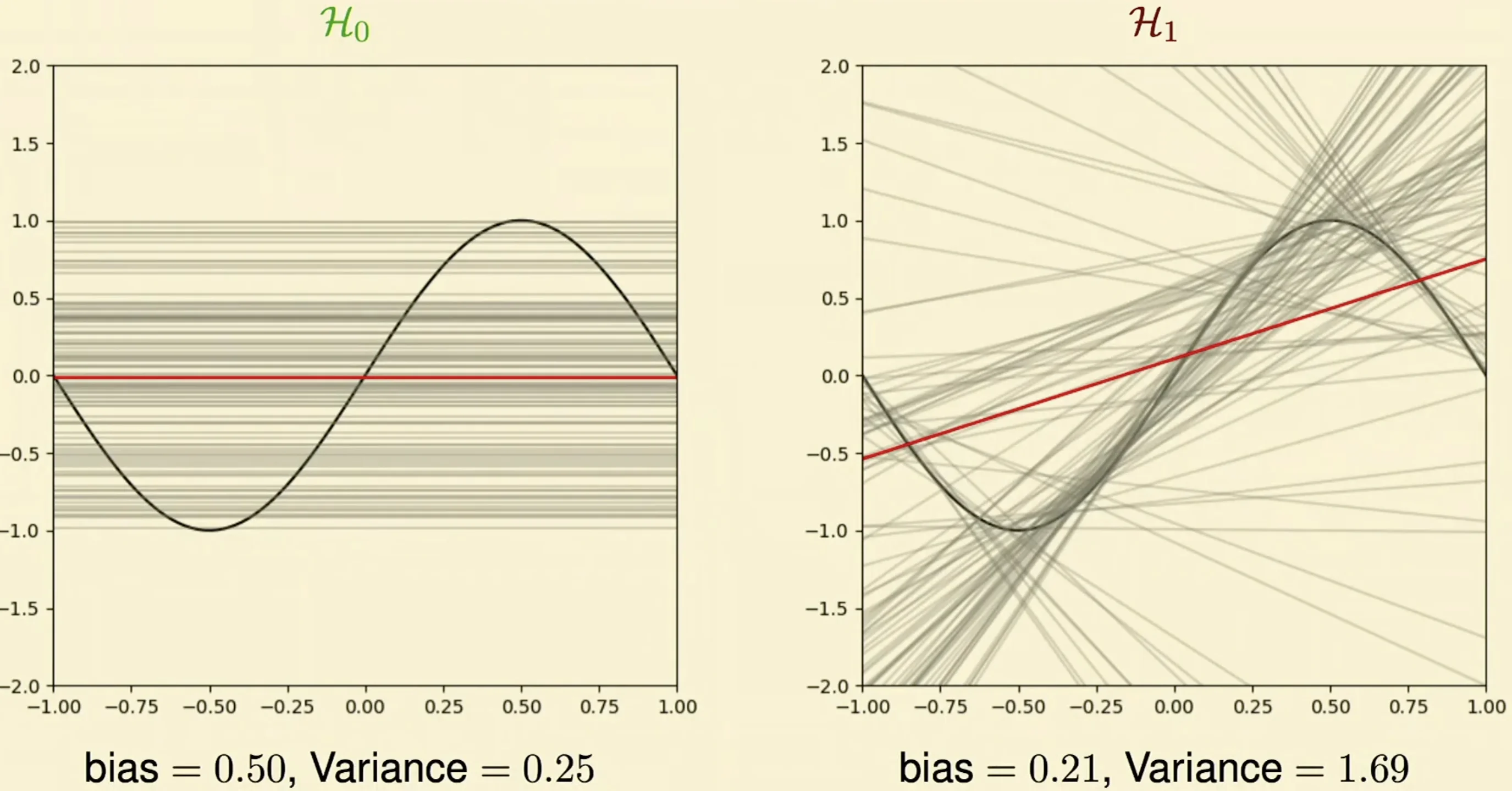
Bias Variance

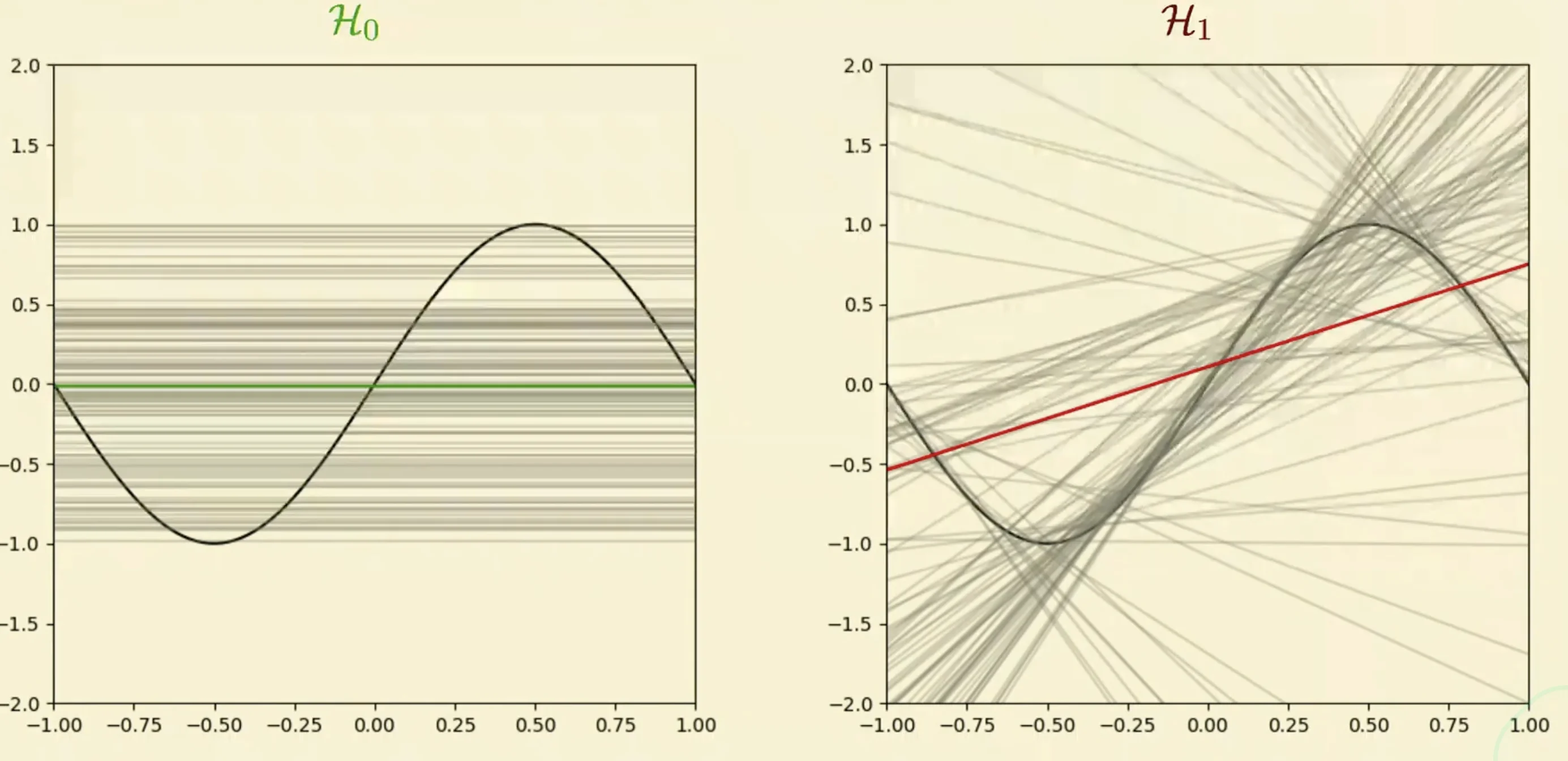
clipboard.png

  • From each possible models, we calculate the expected model (mean)
  • From the mean model, we calculate the variance and the bias

clipboard.png

Learning in Practice

  • more training examples with noise

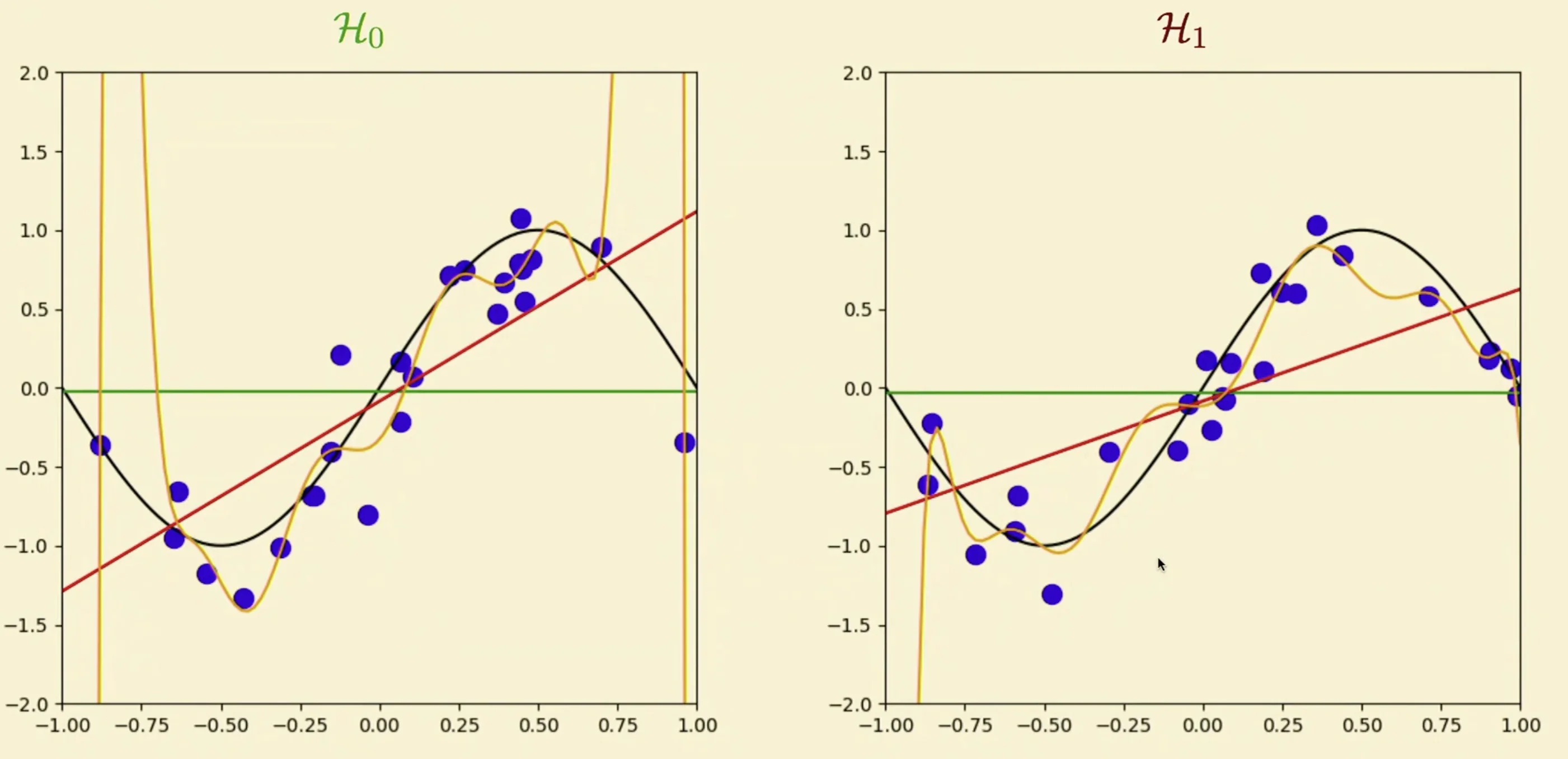
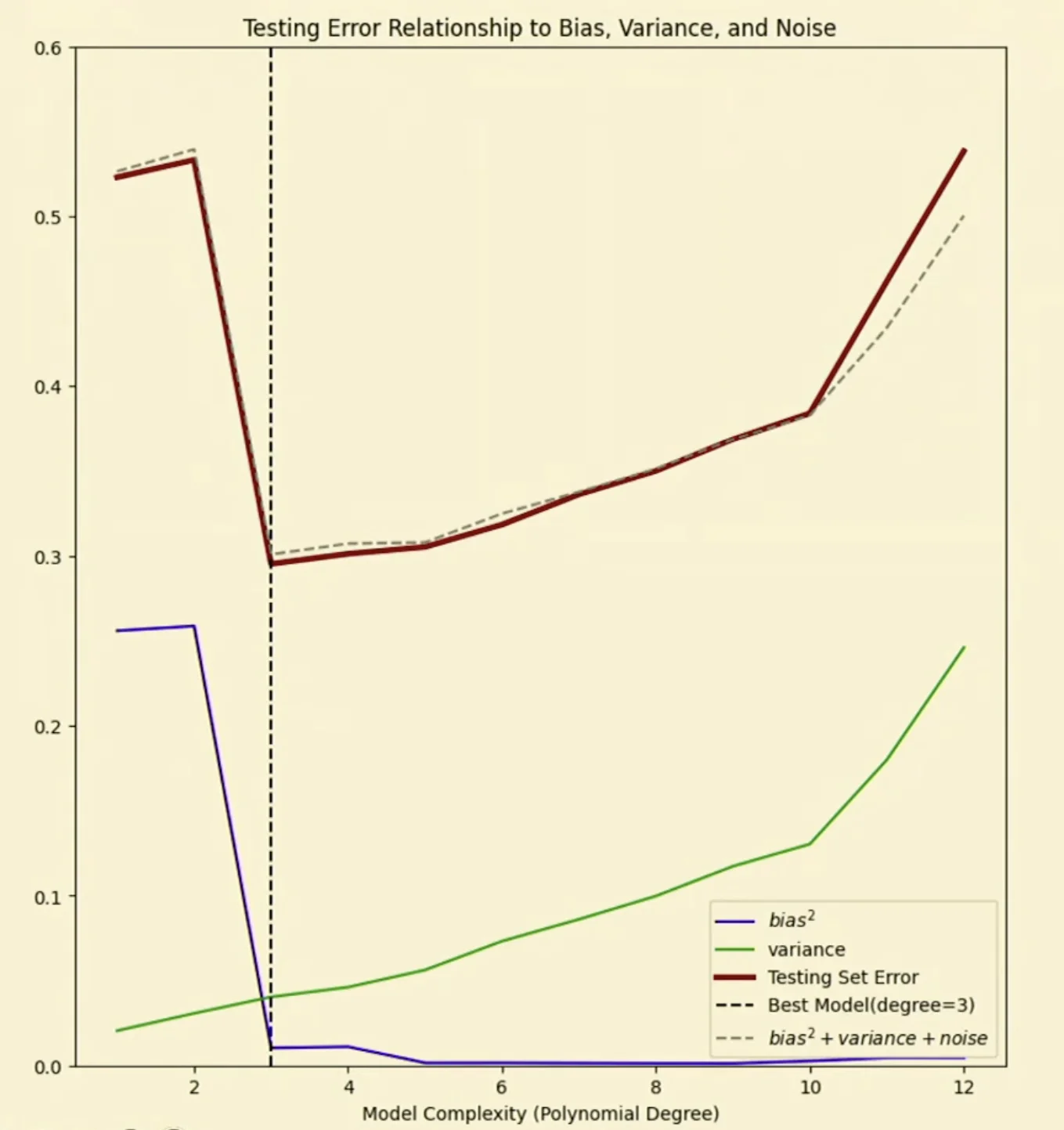
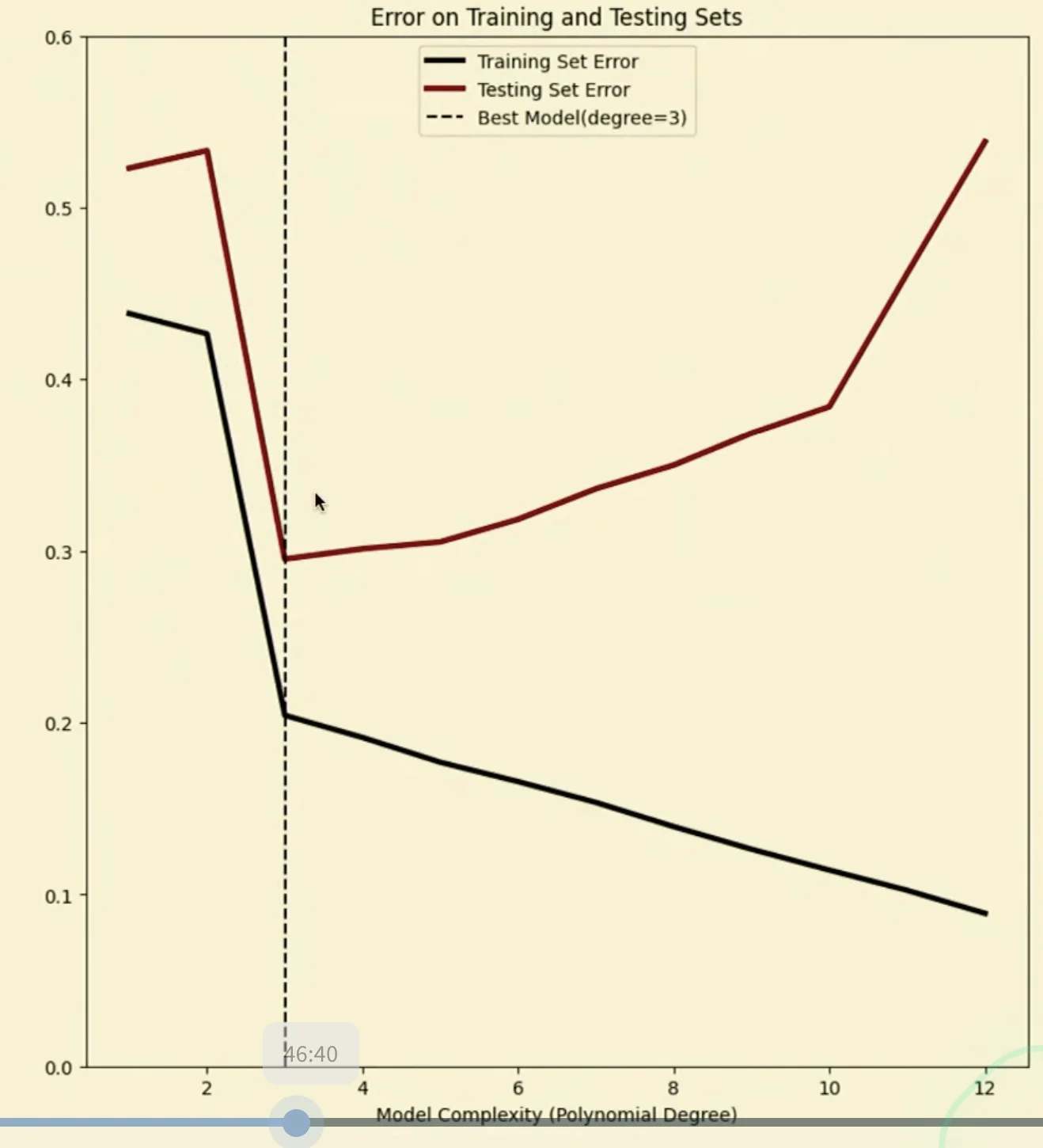
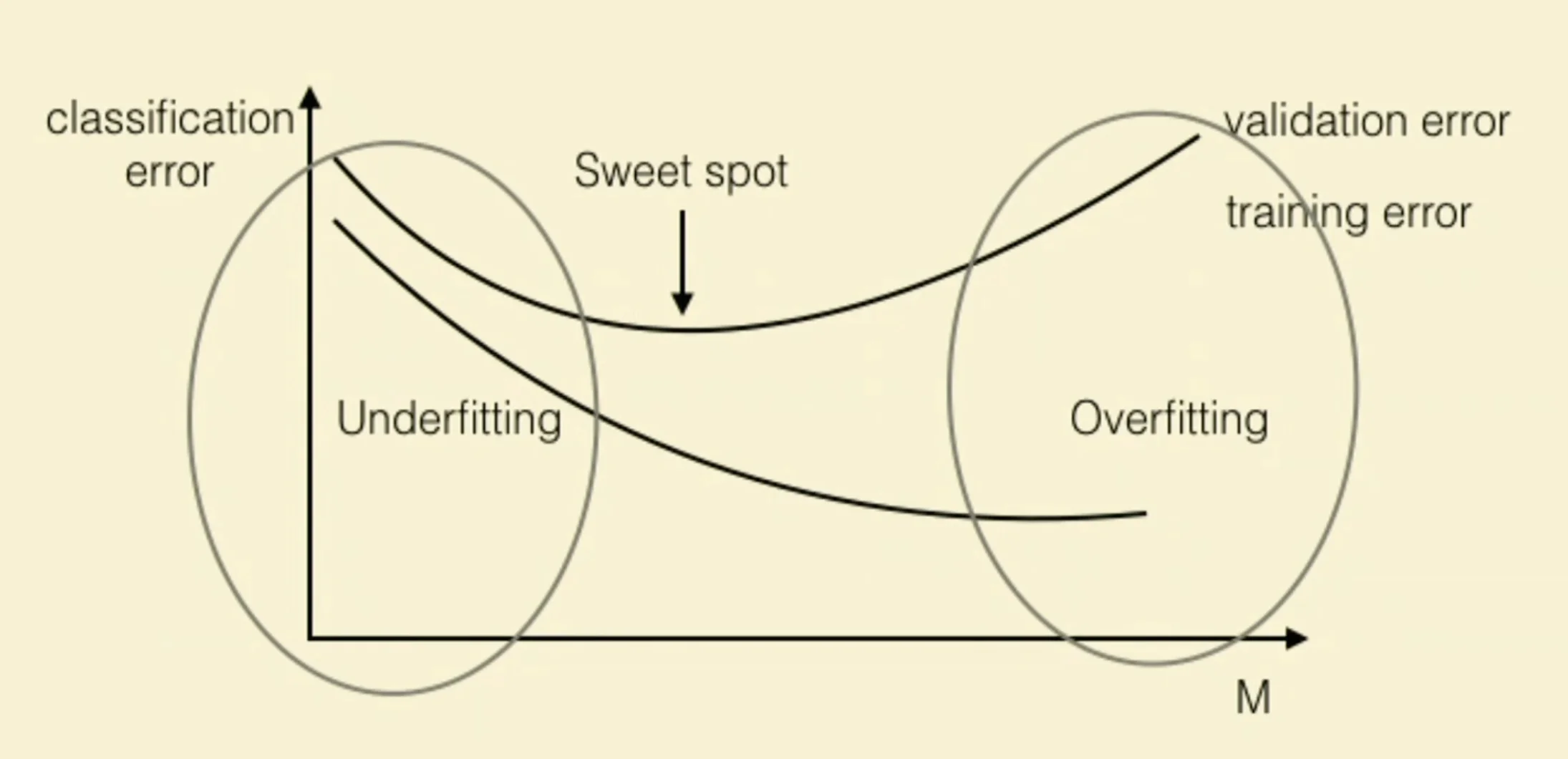
clipboard.png clipboard.png clipboard.png

  • Models to the left of best model may underfit
  • Models to the right of the best model may overfit

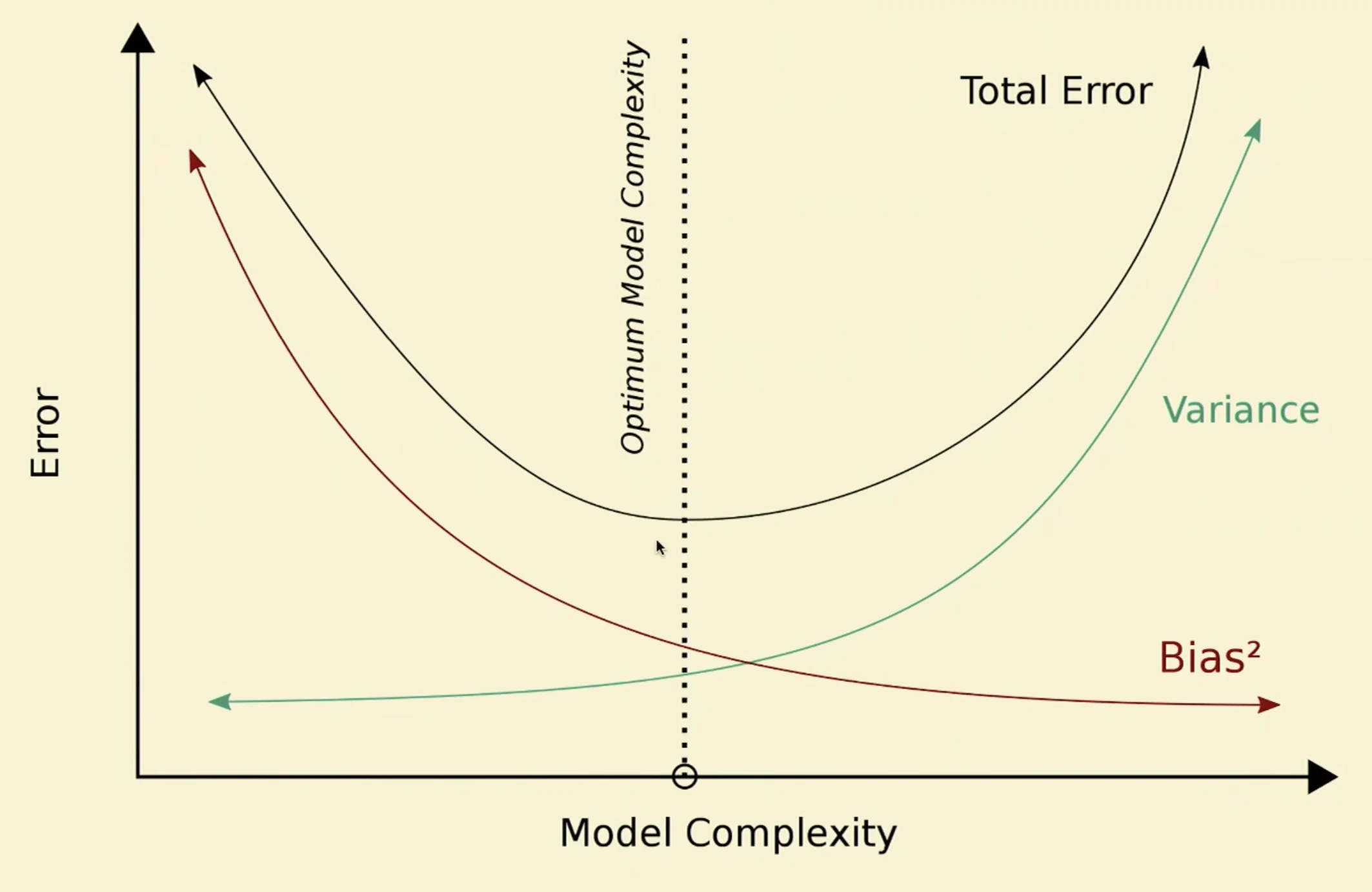
clipboard.png

REM and Overfitting and Underfitting

REM=min⁡w1N∑i=1Nl(hw(x(i)),y(i))+λγ(w)REM = \min_w \frac{1}{N} \sum^N_{i = 1}l(h_w(x^{(i)}), y^{(i)}) + \lambda \gamma(w)

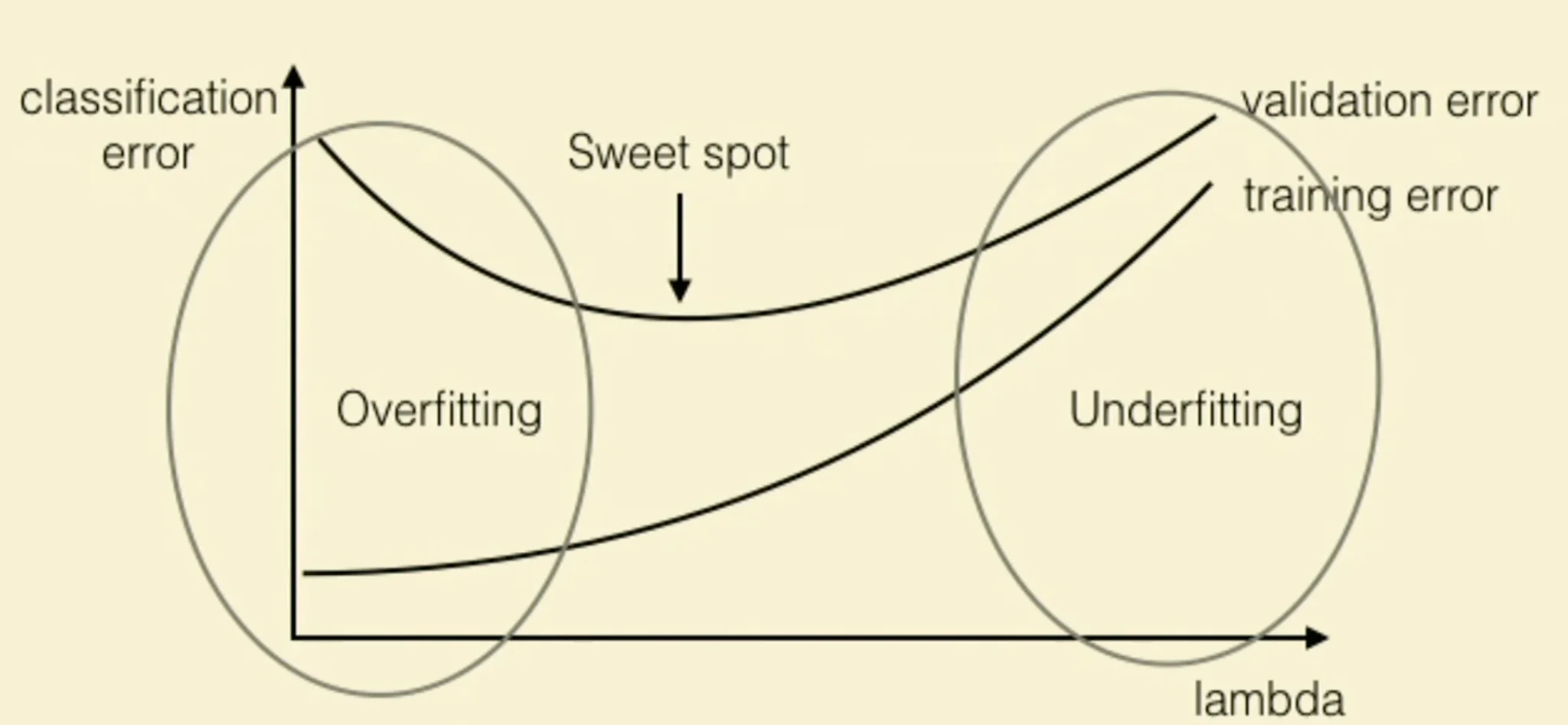
clipboard.png

Important

Hoow to identify the sweet spot?

Hold-out Method

How

  • Can judge test error by using an independent sample of data
  • Split data into training set and validation set
  • Use the two sets for training and testing respectively.

Important

Telescopic Search

Find the best order of magnitude (λ)(\lambda)

Drawback

  • May not have enough data to afford setting one subset aside for getting generalizability
  • Validation error may be misleading (bad estimate of test error) if we get an unfortunate split

K-Fold Cross-Validation

  • Create K-fold partition of the dataset

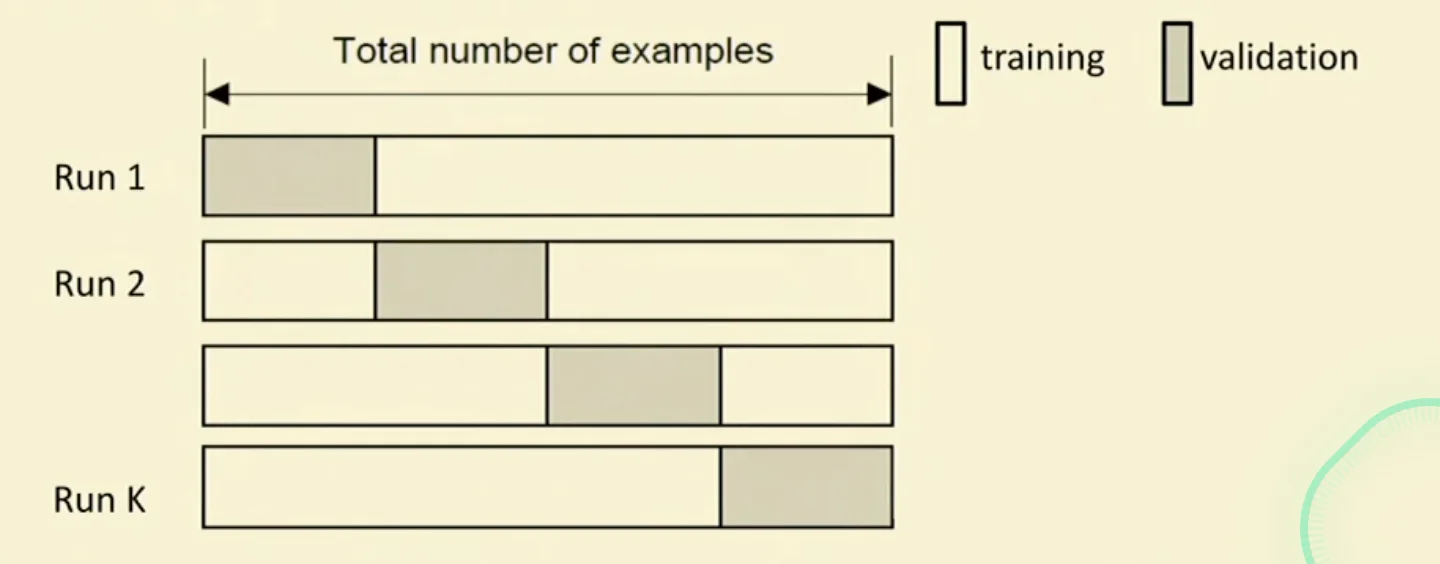
clipboard.png

  • Train using K−1K - 1 partitions and calculate the validation error using the remaining partition

Large K

  • Validation error can approximate test error well
  • Observed validation error will be unstable (few validation points)
  • The computational time will be very large as well

Small K

  • The # of runs and computational time are reduced
  • Observed validation error will be stable
  • Validation error cannot approximate test error well

Tip

K=10K = 10 is a common choice.

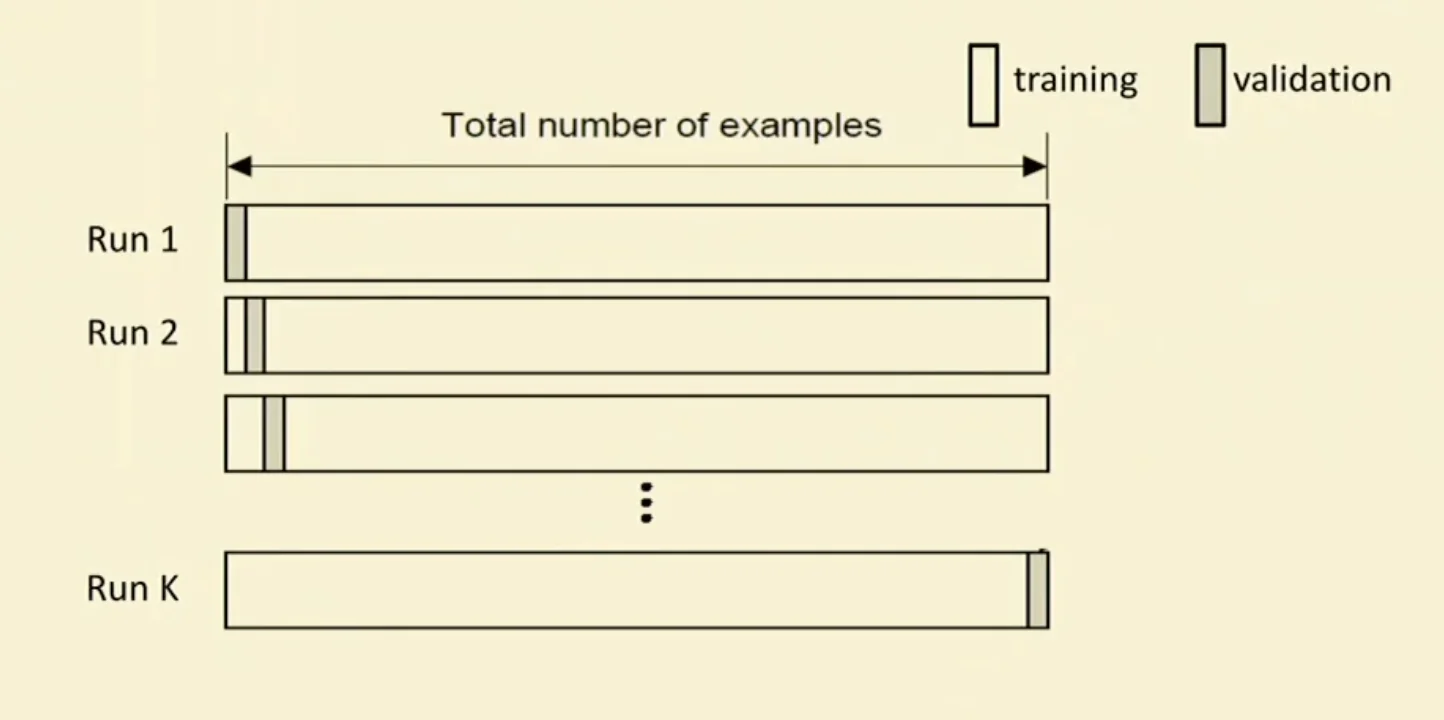
Leave-One-Out (LOO) Cross-Validation

  • Special case of K-fold validation with K=NK = N partitions

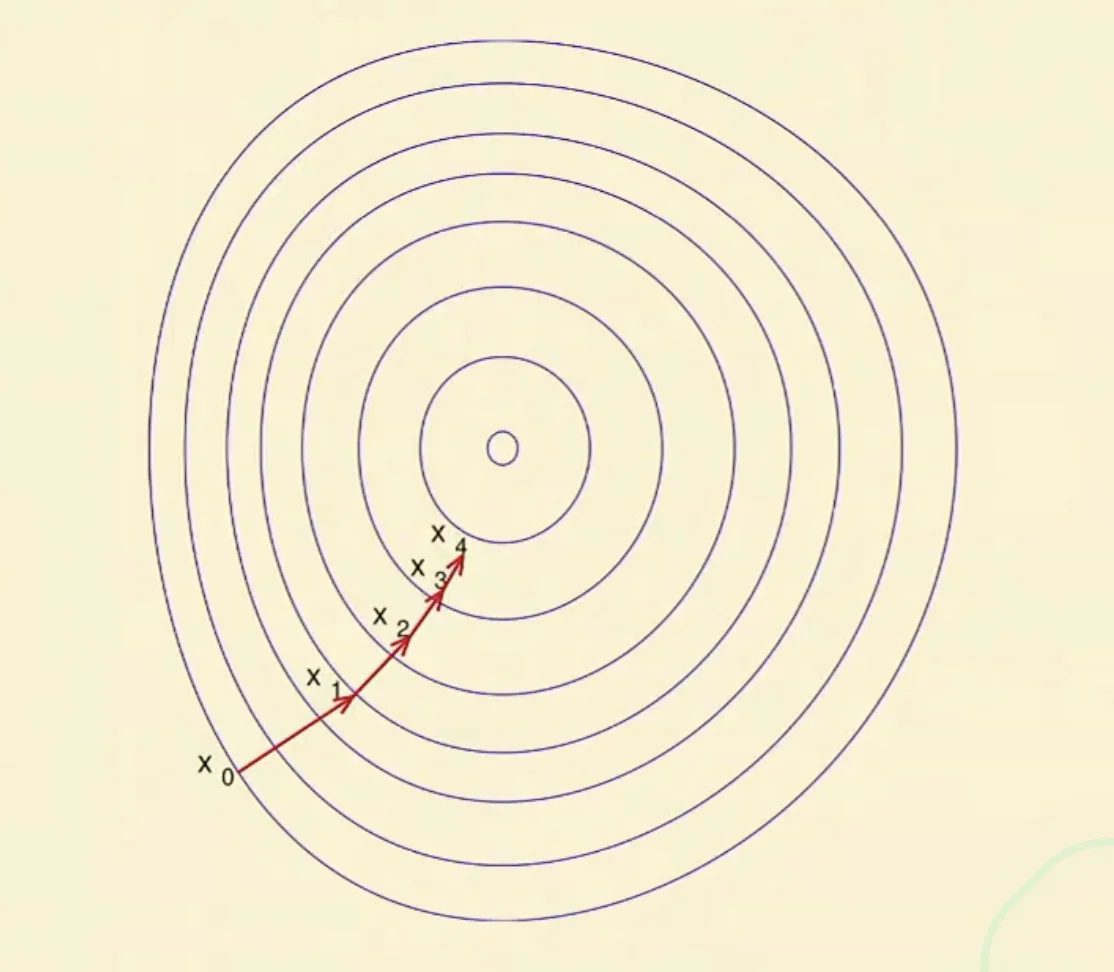
clipboard.png

Early Stopping

  • Stop your optimization after M≥0M \ge 0 number of gradient steps, even if optimization has not converged yet.

What’s the connection between early stopping and regularization?

Early Stopping

clipboard.png

Regularization

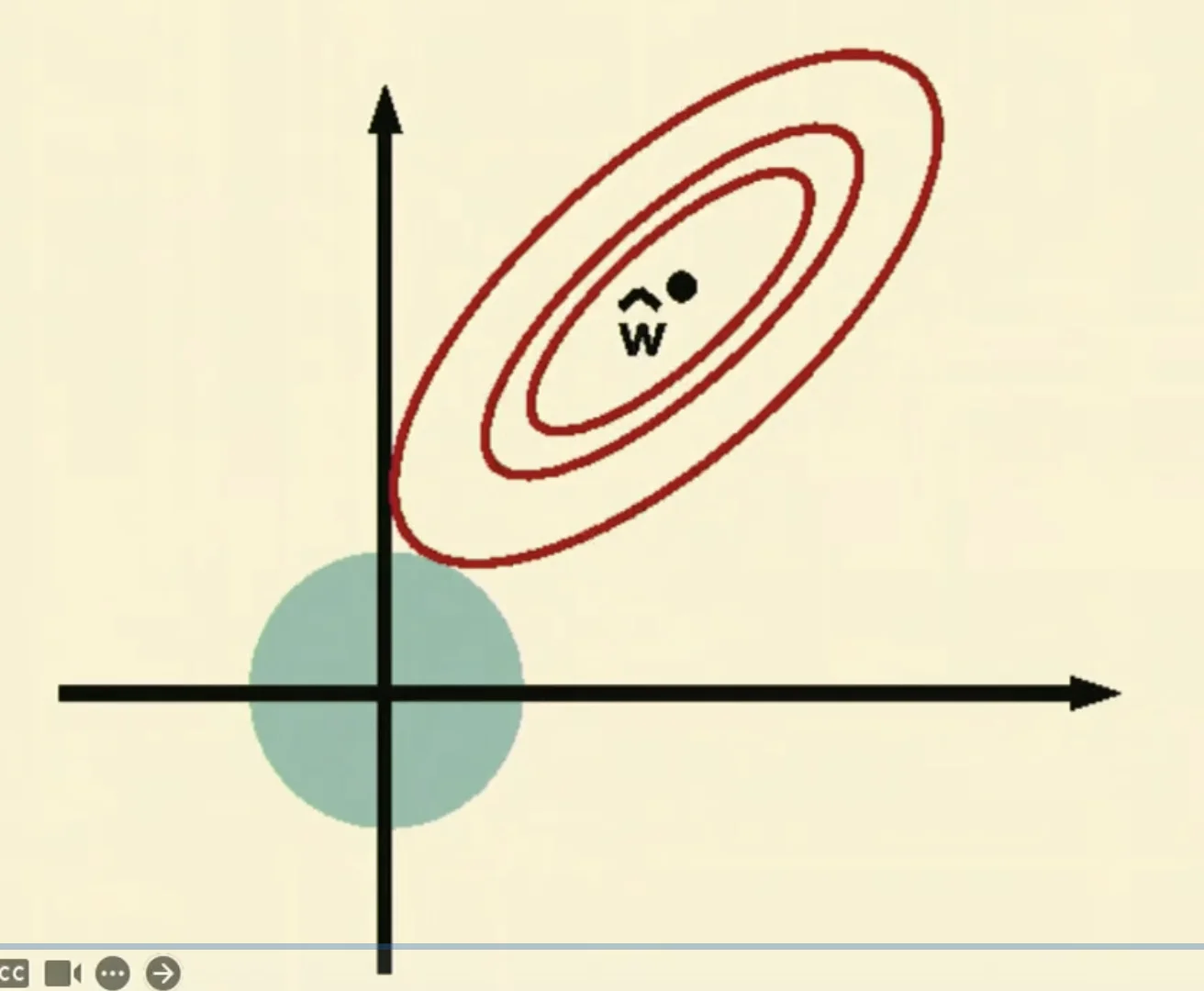
clipboard.png

  • Regularization restricts the predictions going outside of the green area.

The plot of early stopping

clipboard.png

Think about the variance

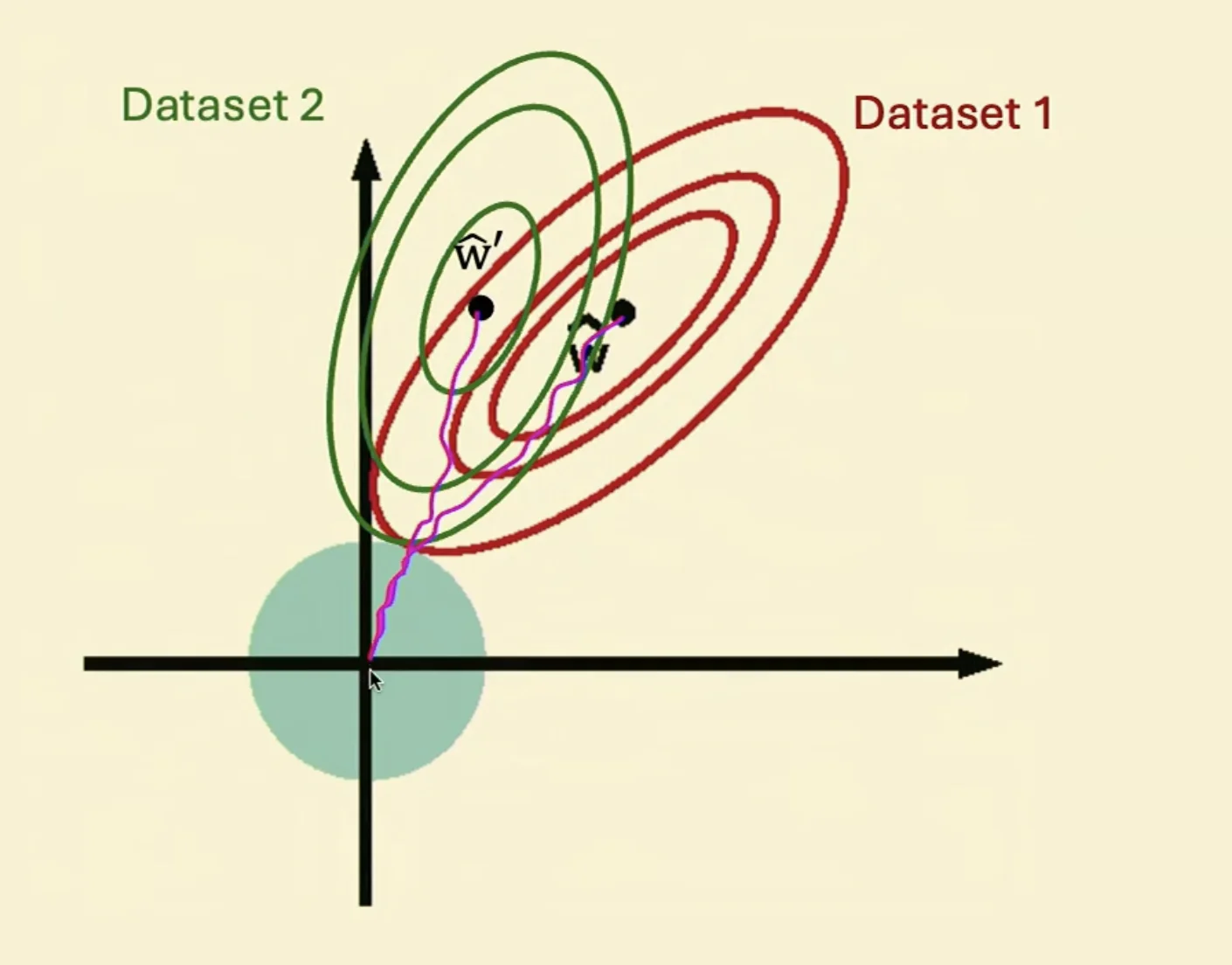
clipboard.png

  • If we stop early, we can stop the variance caused by different dataset