Fourier Series - Prelude
∙ From Sinusoid (sin(kx)) to Square Wave
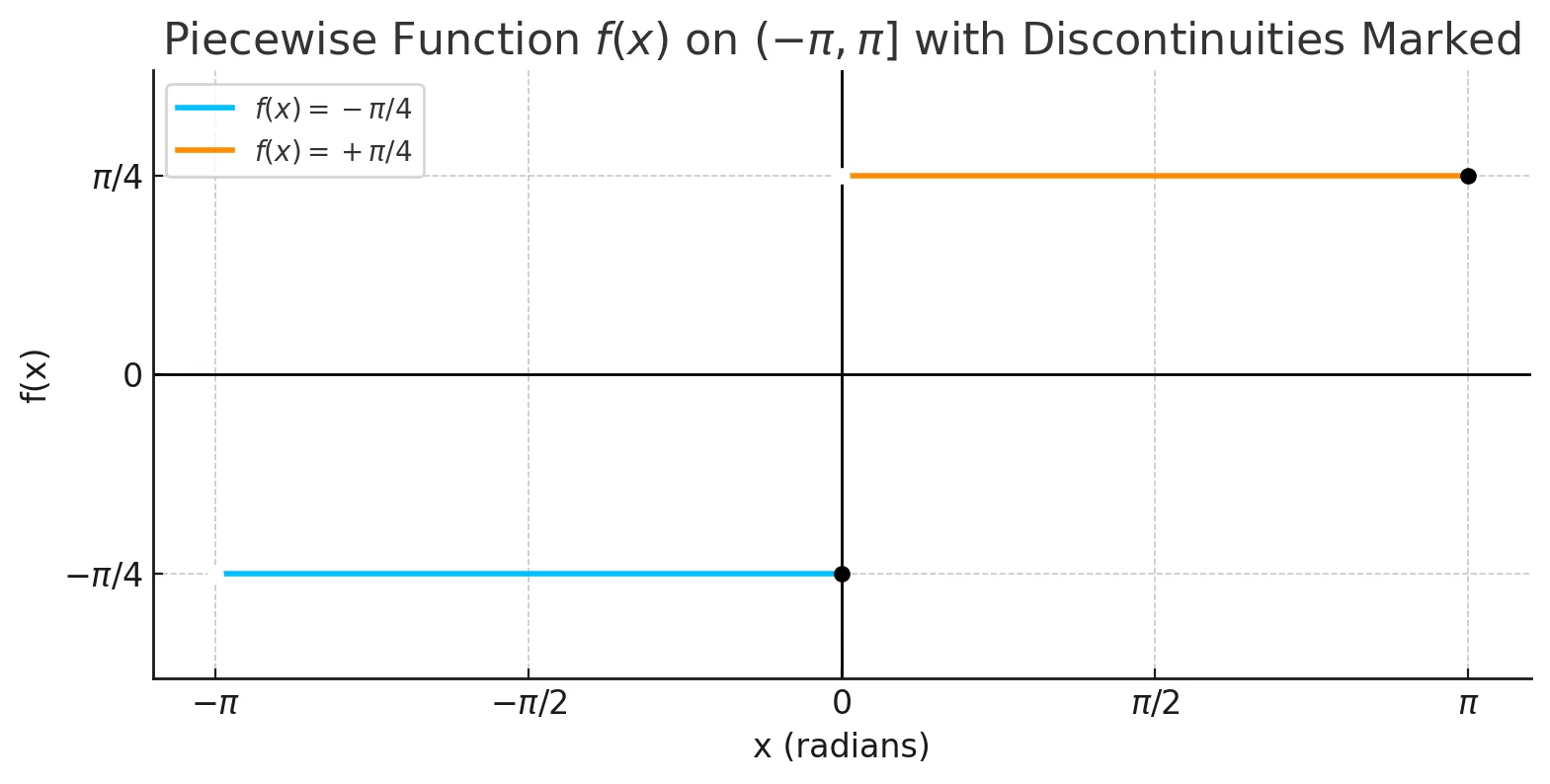
1. Assume a function y=f(x)
- defined on (−π,π]
- discontinuous at x=0
y=f(x)={−4π4π(−π<x≤0)(0<x≤π)
2. The Fourier Series of sin(kx)
y=f(x)=k=1∑∞bksin(kx)⋅where bk={b2k=0b2k−1=2k−11
3. Expand y
y=f(x)=k=1∑∞2k−11sin(2k−1)x=sinx+31sin3x+51sin5x+…
- The shapes of three sinusoids
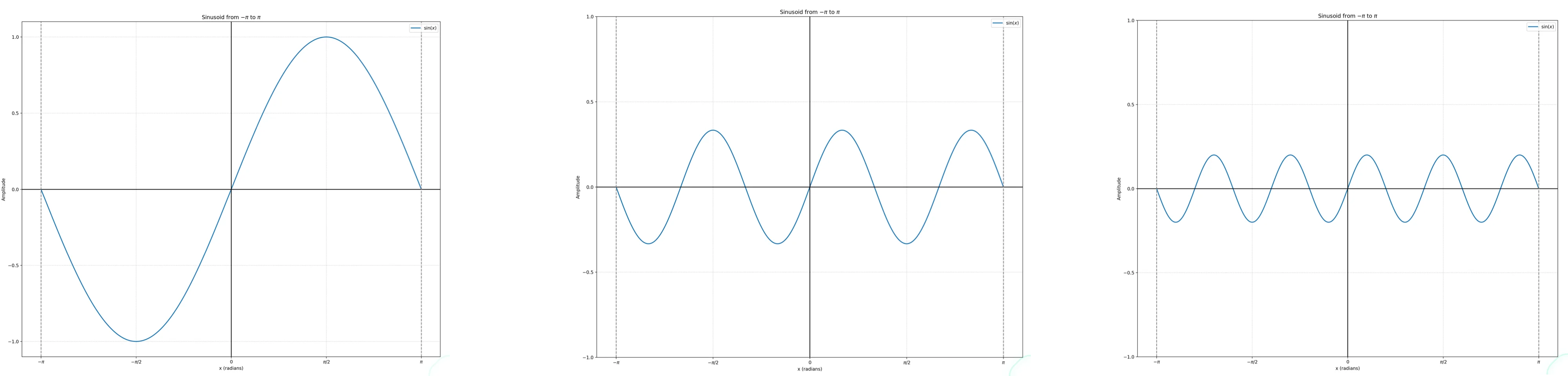
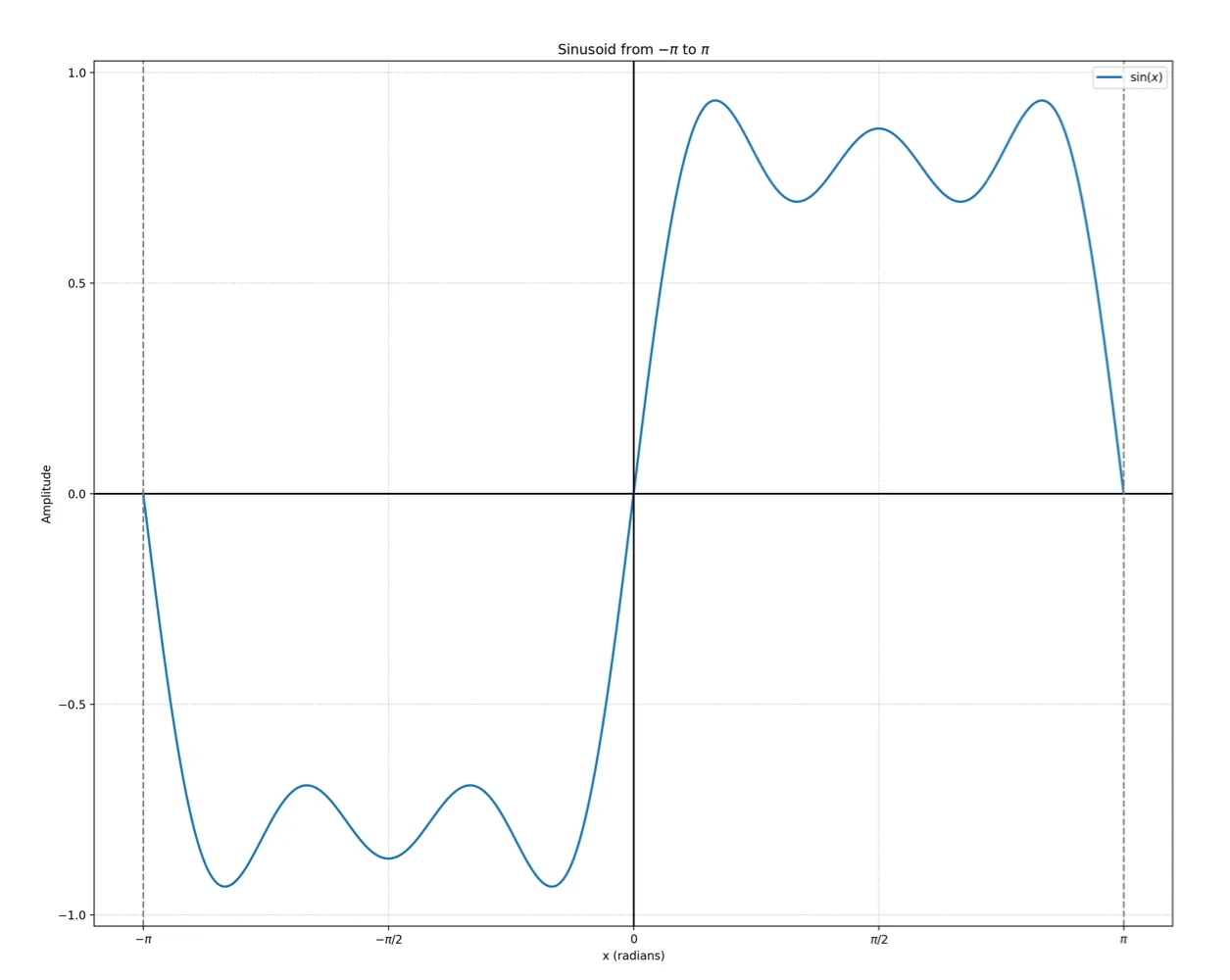
- sinx+31sin3x+51sin5x
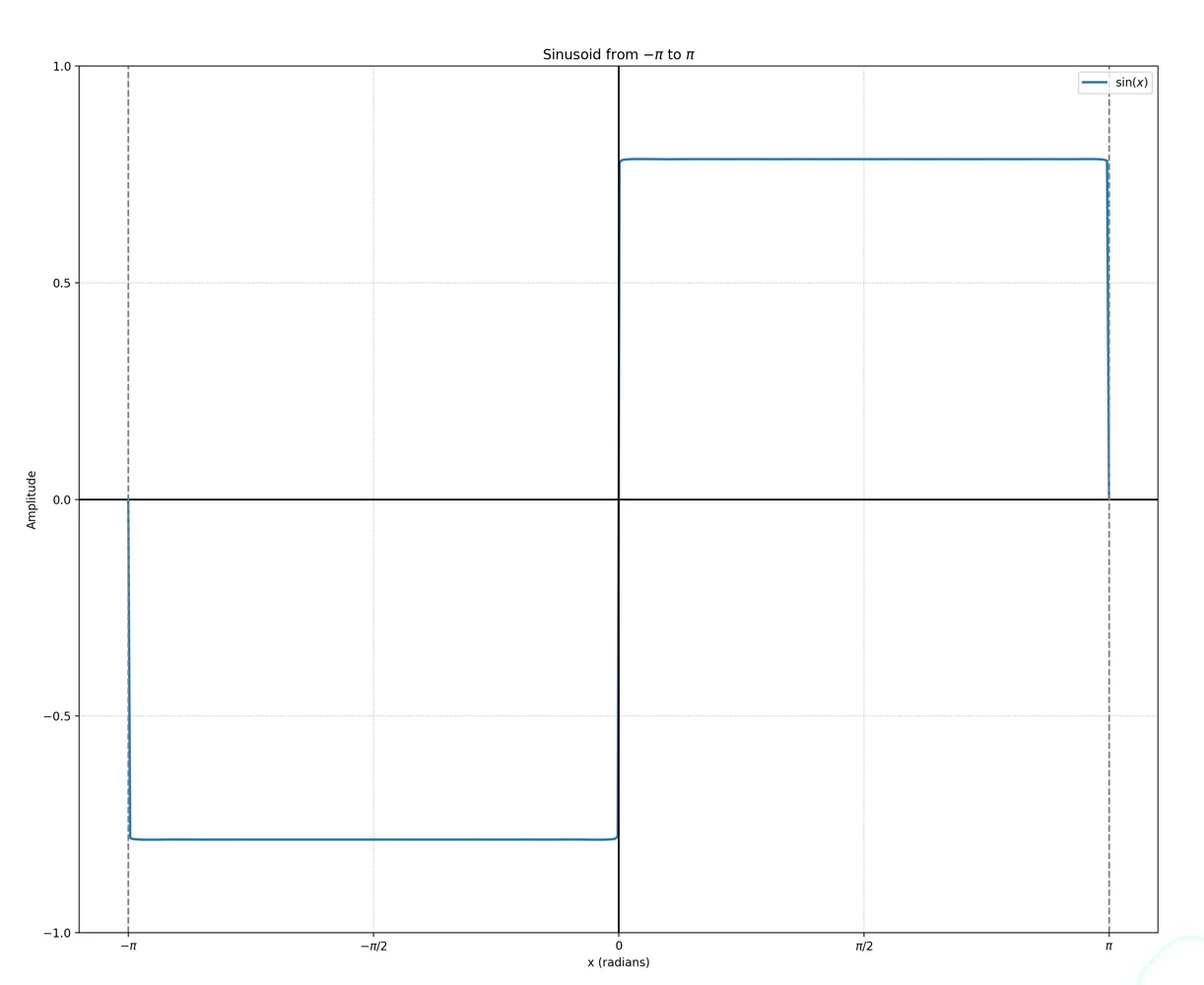
- ∑k=1100002k−11sin(2k−1)x
Tip
- As we accumulate more sinusoids, f(x) approaches a square wave
- n=300 is the boundary where our eyes can barely tell the difference between sinusoids and a square wave
Gibb’s Phenomenon

- Overshoot occurs near the jump of discontinuity in the singal
- It’s an error with about 9% of the jump size
- It’s fixed when n→∞
Trignometry Recap
1. Properties
⋅ Even function
cos(−x)=cos(x)
⋅ Odd function
sin(−x)=−sin(x)tan(−x)=−tan(x)
2. Basic Formulas
(i)(ii)(iii)cos2x+sin2x=1tanx=cosxsinx1+tan2x=cos2x1
3. Addition Theorem
(i)(ii)cos(α±β)=cosα⋅cosβ∓sinα⋅sinβsin(α±β)=sinα⋅cosβ±cosα⋅sinβ
4. Double Angle Formulas
cos2α=cos2α−sin2α=2cos2α−1=1−2sin2α
sin2α=2sinα⋅cosα
5. Half Angle Formulas
(i)(ii)cos2α=2(1+cos2α)sin2α=2(1−cos2α)
6. Product → Sum Formulas
(i)(ii)(iii)cosα⋅cosβ=21{cos(α+β)+cos(α−β)}sinα⋅sinβ=21{cos(α+β)−cos(α−β)}sinα⋅cosβ=21{sin(α+β)−sin(α−β)}
Periodic Functions
- Given x∈R and ∃L∈K, f(x) is a periodic function of 2L
f(x+2L)=f(x)
1. sin(kx)
- The period of sin(x) is 2π
y=sin(x)⇒L=2πy=sin(2x)⇒L=22πy=sin(3x)⇒L=32π…y=sin(kx)⇒L=k2π
- By adding every multiple the period, we derive a function with L=2π
y=k=1∑∞bksin(kx)
2. Approximate the Function of Square Wave
Square Wave
y=f(x)(−π<x≤π)={4−π4π(−π<x≤0)(0<x≤π)

Fourier Series
y=k=1∑∞2k−1sin(2k−1)x
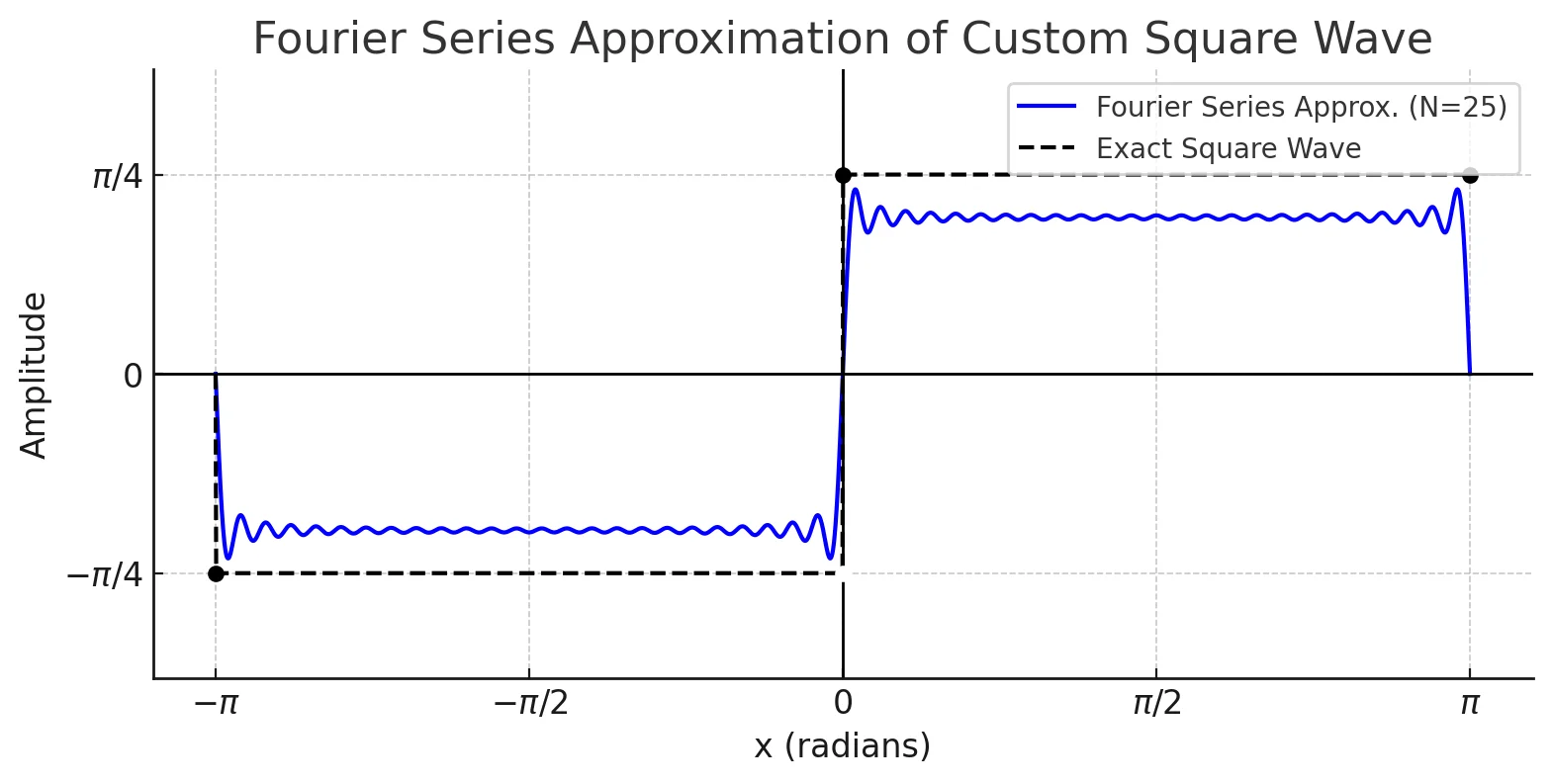
Tip
- Both functions have the period of 2π
- The discontinuities are shown with Gibb’s Overshoot.
Even and Odd Functions
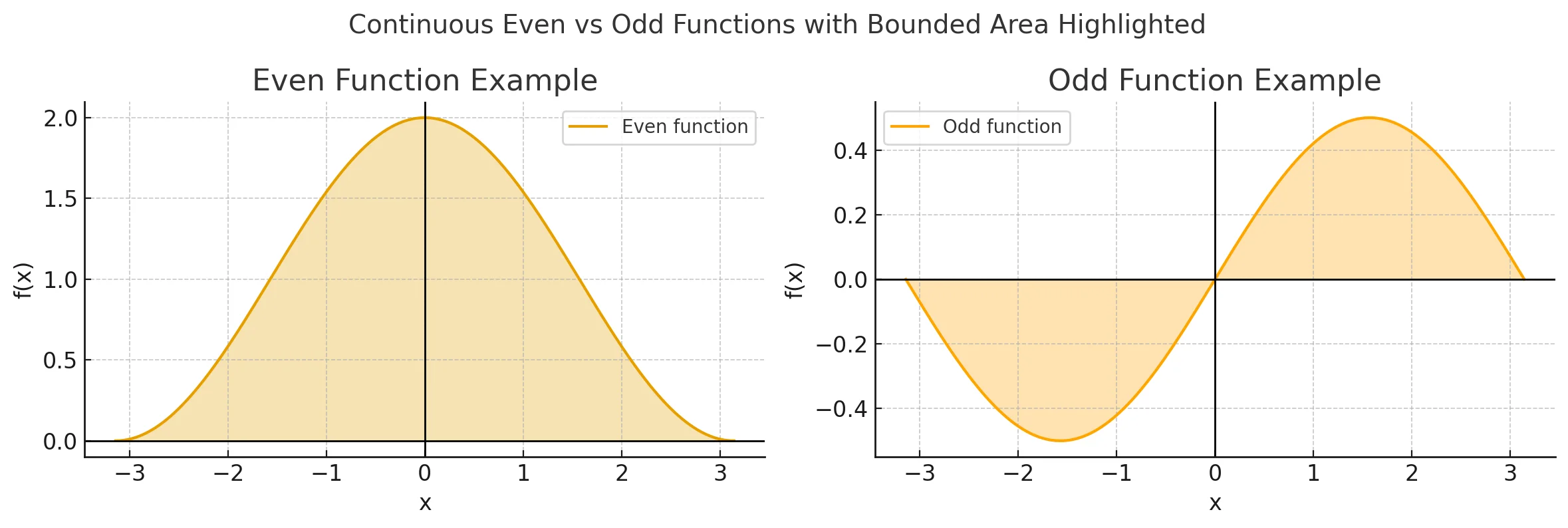
1. Even function
⋅f(−x)=f(x)⋅∫−aaf(x)dx=2∫0af(x)dx
∫−ππcos(x)dx=2∫0πcos(x)dx
2. Odd function
⋅f(−x)=−f(x)⋅∫−aaf(x)dx=0
∫−ππsin(x)dx=0
Important
Properties
⋅even×even=even⋅odd×odd=even⋅even×odd=odd
Trignometry and Integration
∫−ππcos(mx)dx=0∫−ππsin(mx)dx=0∫−ππsin(mx)⋅cos(nx)dx=0∫−ππcos(mx)⋅cos(nx)dx={π(m=n)0(m=n)∫−ππsin(mx)⋅sin(nx)dx={π(m=n)0(m=n)
where
- n,m∈N
(1) Integration of the sin and cos functions
⋅∫−ππcos(mx)dx=0
∫−ππcos(mx)dx=m1[sin(mx)]−ππ=m1[sin(mπ)−sin(−mπ)]=m1[sin(mπ)+sin(mπ)]∵sin(mπ)=0∴m1[sin(mπ)+sin(mπ)]=0⇒0
⋅∫−ππsin(mx)dx=0
∫−ππsin(mx)dx=−m1[cos(mx)]−ππ=−m1[cos(mπ)−cos(−mπ)]=−m1[cos(mπ)−cos(mπ)]∵cos(mπ)=−1∴m1[cos(mπ)+cos(mπ)]=0⇒0
(2) ∫−ππsin(mx)⋅cos(nx)dx=0
∫−ππodd funcsin(mx)⋅even funccos(nx)dx∵odd×even=odd∴∫−ππsin(mx)⋅cos(nx)dx=0
(3) ∫π_−πcos(mx)⋅cos(nx)dx={π(m=n)0(m=n)
⋅(m=n)
∫−ππcos(mx)⋅cos(nx)dx=∫−ππcos2(mx)dx=∫−ππcos2(mx)dx(Half angle formula)=21[∫−ππdx+0∫−ππcos(2mx)dx]=π+0=π
⋅(m=n)
∫−ππcos(mx)⋅cos(nx)dx=21∫−ππcos(mx+nx)+cos(mx−nx)dx=21[∫−ππcos(mx+nx)+∫−ππcos(mx−nx)dx]=21[0∫−ππcos(m+n)xdx+0∫−ππcos(m−n)xdx]=0
(4) ∫−ππsin(mx)⋅sin(nx)dx={π(m=n)0(m=n)
Tip
The proof is the same as the one given in (3)
Inner Product and Norm
- Given two functions f and g that are continuous on the closed interval [−π,π]
⋅The inner product of f and g: (f,g)=∫−ππf(x)g(x)dx
⋅The norm (magnitude) of f is: ∣∣f∣∣=(f,f)=∫−ππ{f(x)}2dx
Orthogonality relations of trigonometric functions
- Constant vs. cosine and sine
∫−ππcos(mx)dx=0⇒(1,cos(mx))=0
∫−ππsin(mx)dx=0⇒(1,sin(mx))=0
So, the constant function 1 is orthogonal to both cos(mx) and sin(mx).
- Sine vs. cosine
∫−ππsin(mx)cos(nx)dx=0⇒(sin(mx),cos(nx))=0
Thus, sine and cosine are orthogonal to each other.
- Cosine vs. cosine
∫−ππcos(mx)cos(nx)dx=⎩⎨⎧π0m=nm=n⇒(cos(mx),cos(nx))=⎩⎨⎧π0m=nm=n
- Sine vs. sine
∫−ππsin(mx)sin(nx)dx=⎩⎨⎧π0m=nm=n⇒(sin(mx),sin(nx))=⎩⎨⎧π0m=nm=n









