Hessian

Definition

If you have a real-valued function

f:Rd→Rf: \R^d \rightarrow \R

The Hessian matrix of f at a point w∈Rd\textbf{w} \in \R^d is the square matrix of all second-order partial derivaties:

H(w)=∇2f(w)=[∂2f∂w12∂2f∂w1∂w2⋯∂2f∂w1∂wd∂2f∂w2∂w1∂2f∂w22⋯∂2f∂w2∂wd⋮⋮⋱⋮∂2f∂wd∂w1∂2f∂wd∂w2⋯∂2f∂wd2]H(w) = \nabla^2f(w) = \begin{bmatrix} \frac{\partial^2 f}{\partial w_1^2} & \frac{\partial^2 f}{\partial w_1 \partial w_2} & \cdots & \frac{\partial^2 f}{\partial w_1 \partial w_d} \\ \frac{\partial^2 f}{\partial w_2 \partial w_1} & \frac{\partial^2 f}{\partial w_2^2} & \cdots & \frac{\partial^2 f}{\partial w_2 \partial w_d} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial w_d \partial w_1} & \frac{\partial^2 f}{\partial w_d \partial w_2} & \cdots & \frac{\partial^2 f}{\partial w_d^2} \end{bmatrix}
  • Entry Hij=∂2f∂wi∂wjH_{ij} = \frac{\partial^2 f}{\partial w_i \partial w_j}
  • If ff is smooth, the Hessian is symmetric (Hab=Hba)(H_{ab} = H_{ba})

Tip

What does “smooth” mean?

f∈C2(Rd)f \in C^2(\R^d)
  • ff has continuous first and second derivatives s.t.
∂2f∂wi∂wj=∂2f∂wj∂wi∀i,j\frac{\partial^2 f}{\partial w_i \partial w_j} = \frac{\partial^2 f}{\partial w_j \partial w_i} \quad\quad \forall i, j

Geometric Meaning

  • The gradient ∇f(w)\nabla f(w) tells you the slope/direction of the steepest ascent

  • The HessianHessian tells you about the curvature

  • How much the slope changes as you move

  • Whether the current surface bends upwards (convex), downwards (concave), or in a saddle point.

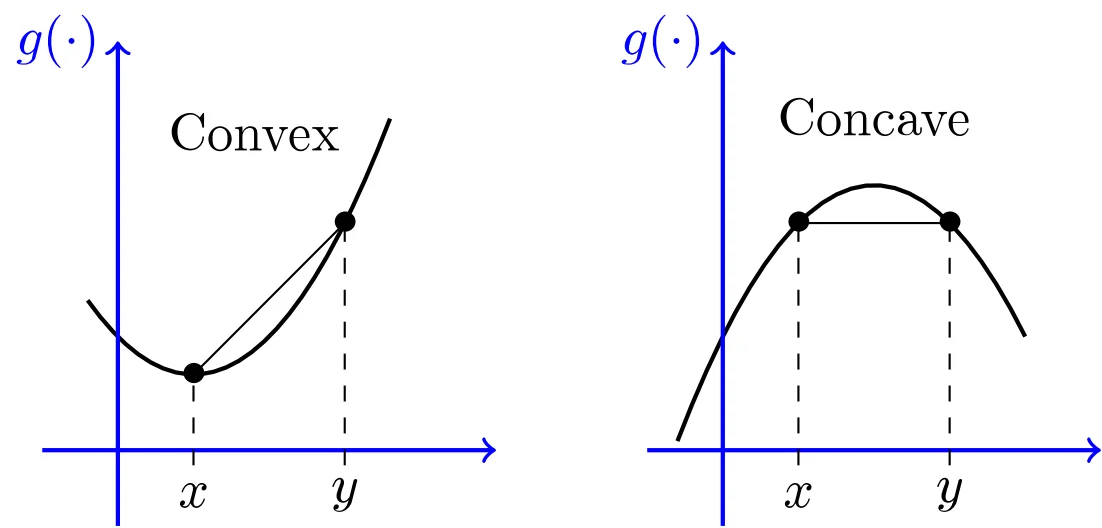
clipboard.png

Tip

Second derivative test

  • Univariate
{concave, local maximum(f′′(x)<0)convex, local mimimum(f′′(x)>0)saddle point(f′′(x)=0)\begin{cases} \text{concave, local maximum}\quad (f''(x) < 0) \\ \text{convex, local mimimum}\quad (f''(x) > 0) \\ \text{saddle point}\quad (f''(x) = 0) \\ \end{cases}

  • Multivariate

  • The sign of the determinant of the Hessian matrix

  • Or D=fxxfyy−fxy2D = f_{xx}f_{yy} - f_{xy}^2

{D=0(inconclusive)D<0(saddlepoint)D>0,fxx>0(local minimum)D>0,fxx<0(local maximum)\begin{cases} D = 0 \quad (inconclusive) \\ D < 0 \quad (saddle point) \\ D >0, f_{xx} > 0 \quad (local\ minimum) \\ D >0, f_{xx} < 0 \quad (local\ maximum) \end{cases}

Definiteness and Curvature

A way to classify the nature of a point

  • Positive Definite (PD)
    • z⊺Hz>0,∀z≠0z^\intercal Hz > 0, \forall z \ne 0
    • function curves upward everywhere (local minimum)
  • Negative Definite (ND)
    • z⊺Hz<0,∀z≠0z^\intercal Hz < 0, \forall z \ne 0
    • function curves downwards everywhere (local maximum)
  • Positive Semi-definite (PSD)
    • z⊺Hz≥0,∀z≠0z^\intercal Hz \ge 0, \forall z \ne 0
    • function curves upward (convex) but may be flat in some directiosn
  • Negative Semi-definite (NSD)
    • z⊺Hz≤0,∀z≠0z^\intercal Hz \le 0, \forall z \ne 0
    • function curves downward (concave) but may be flat in some directiosn
  • Indefinite
    • Some directions curve up, others down.
TypeQuadratic formEigenvalues conditionGeometry
Positive definite (PD)(>0)(>0) for all (z≠0)(\mathbf z\neq 0)All (λ>0)(\lambda > 0)Strict convex bowl
Positive semi-definite (PSD)(≥0)(\geq 0) for all (z)(\mathbf z)All (λ≥0)(\lambda \geq 0)Convex, flat possible
Negative definite (ND)(<0)(<0) for all (z≠0)(\mathbf z\neq 0)All (λ<0)(\lambda < 0)Strict concave dome
Negative semi-definite (NSD)(≤0)(\leq 0) for all (z)(\mathbf z)All (λ≤0)(\lambda \leq 0)Concave, flat possible
IndefiniteBoth positive and negative valuesMix of + and – eigenvaluesSaddle