What’s that?

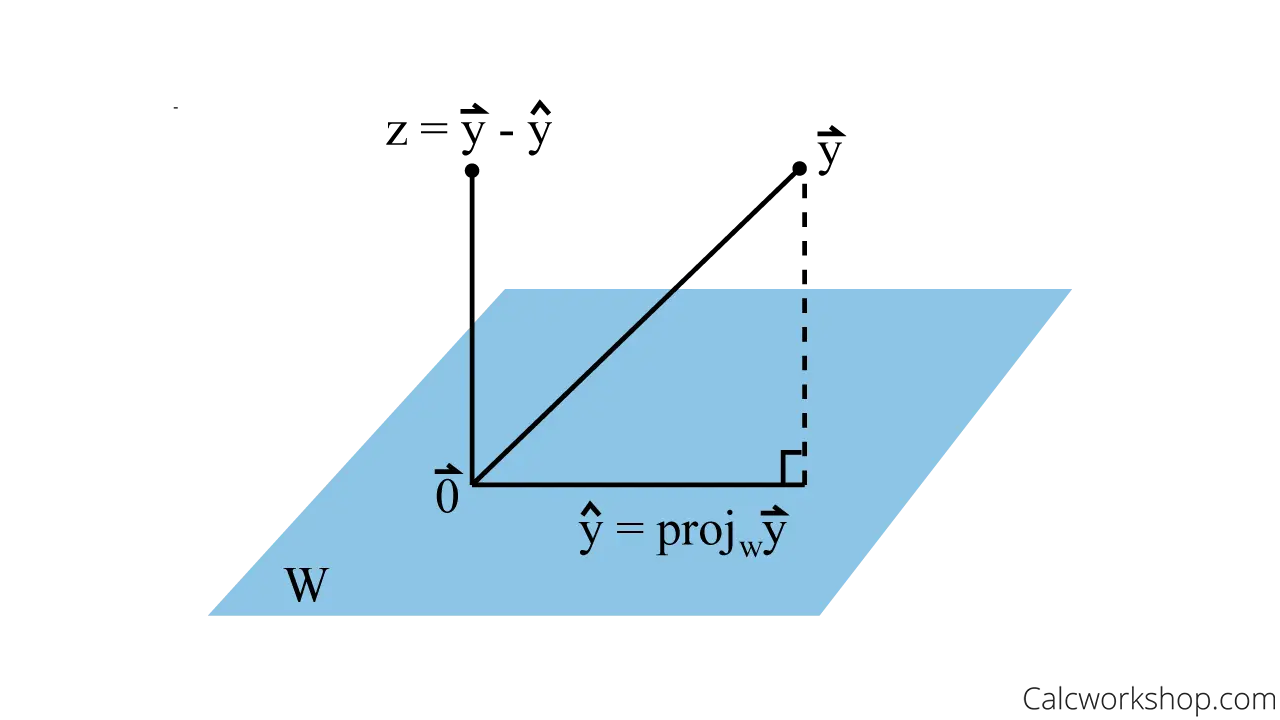
Let VV be a subspace of Rd\R^d. Then any vector w∈Rdw \in \R^d can be uniquely decomposed as:

w=w∣∣+w⊥w = w_{||} + w_{\perp}

where

  • w∣∣∈Vw_{||} \in V
  • w⊥∈V⊥w_{\perp} \in V^\perp
  • V⊥={v∈Rd:v⊺u=0∀u,  u∈V}V^{\perp} = \{v \in \R^d : v^\intercal u = 0 \quad \forall u,\; u \in V\}

Proof

clipboard.png

  • Let V=span{x(i),…,x(N)}V = span\{x^{(i)}, \dots, x^{(N)}\}

1. Define w∣∣w_{||} as an orthogonal projection

w∣∣=projV(w)w_{||} = proj_V(w)
  • projV(w)proj_V(w) is a unique vector that is closest to ww (min⁡v∈V∣∣w−v∣∣)(\min_{v \in V} ||w-v||)

2. Define w⊥w_\perp

w⊥=w−w∣∣w_\perp = w - w_{||}

3. Show w⊥⊥Vw_\perp \perp V

By the properties of orthogonal projection, w⊥w_\perp is orthogonal to every vector in VV.

w⊥⊺x(j)=(w−w∣∣)⊺x(j)=0w_\perp^\intercal x^{(j)} = (w - w_{||})^\intercal x^{(j)} = 0

Express w∣∣w_{||} in terms of basis vector

Since w∣∣∈V=span{x(1),…,x(N)}w_{||} \in V = span\{x^{(1)}, \dots, x^{(N)}\}, by definition of span:

w∣∣=∑j=1Nα(j)x(j)w_{||} = \sum^N_{j = 1} \alpha^{(j)}x^{(j)}

for some coefficient α(1),…α(N)∈R\alpha^{(1)}, \dots \alpha^{(N)} \in \R