Beta and Gamma Distribution Proofs

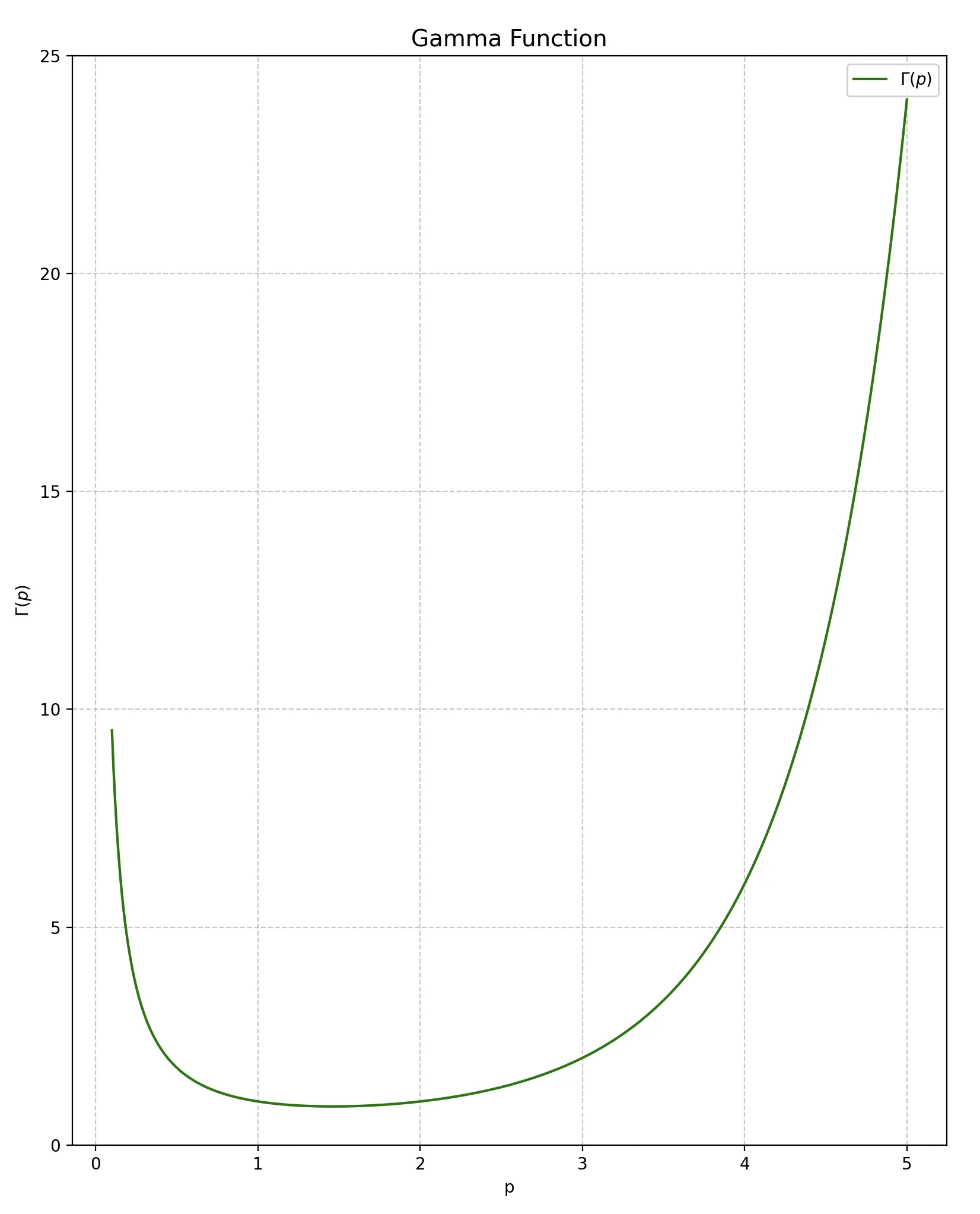
Γ\Gamma Function

Definition

Γ(p)=∫0∞xp−1e−xdx\Gamma(p) = \int^{\infty}_{0} x^{p - 1} e^{-x} dx

clipboard.png

Properties

  • Γ(p+1)=pΓ(p)=p!\Gamma(p + 1) = p\Gamma(p) = p!
  • Γ(1)=1\Gamma(1) = 1
  • Γ(12)=π\Gamma(\frac{1}{2}) = \sqrt{\pi}
  • Γ(n2)={(n2−1)!(n is even)(n2−1)(n2−2)⋯32⋅12π(n is odd)\Gamma(\frac{n}{2}) = \begin{cases} (\frac{n}{2} - 1)! \quad (\text{n is even}) \\ (\frac{n}{2} - 1)(\frac{n}{2} - 2)\cdots \frac{3}{2}\cdot \frac{1}{2}\sqrt\pi \quad (\text{n is odd})\end{cases}

B\Beta Function

B(p,q)=∫01xp−1(1−x)q−1dx(p>0,q>0)\Beta(p, q) = \int^1_0 x^{p - 1} (1 - x)^{q - 1} dx \quad (p > 0, q > 0) B(p,q)=Γ(p)+Γ(q)Γ(p+q)\Beta(p, q) = \frac{\Gamma(p) + \Gamma(q)}{\Gamma(p + q)}

TO-DO: Proof for the gamma form