6. Empirical Risk Minimization (ERM)

Recall: SVM

min⁡w,b12∣∣w∣∣22+C∑i=1Nmax⁡(0,1−y(i)(w⊺x(i)+b))\min_{w, b} \frac{1}{2} ||w||^2_2 + C\sum^N_{i = 1} \max \left(0, 1 - y^{(i)}(w^\intercal x^{(i)} + b)\right)
  • ∣∣w∣∣22||w||^2_2
  • regularizer
  • ∑i=1Nmax⁡(0,1−y(i)(w⊺x(i)+b))\sum^N_{i = 1} \max(0, 1 - y^{(i)}(w^\intercal x^{(i)} + b))
  • loss

Rewrite

min⁡w1N∑i=1Nmax⁡(1−y(i)(w⊺x(i)+b⏟hw(x(i))),0)⏟Hinge Loss+λ∣∣w∣∣22⏟L2−Regularizer\min_w \frac{1}{N} \sum^N_{i = 1} \underbrace{\max (1 - y^{(i)}(\underbrace{w^\intercal x^{(i)} + b}_{h_w(x^{(i)})} ), 0)}_{\text{Hinge Loss}} + \lambda \underbrace{||w||^2_2}_{L2-Regularizer}

Tip

Check out more on SVM in 5. SVM

Loss Function

min⁡w1N∑i=1Nl(hw(x(i)),y(i))+λr(w)\min_w \frac{1}{N} \sum^N_{i = 1} l(h_w(x^{(i)}), y^{(i)}) + \lambda r(w)
  • The loss function l(hw(x),y)l(h_w(x), y) quantifies how badly the estimate hw(x)h_w(x) approximates the real yy
  • Smaller value →\rightarrow good approximation

Risk

min⁡w1N∑i=1Nl(hw(x(i)),y(i))+λr(w)\min_w \frac{1}{N} \sum^N_{i = 1} l(h_w(x^{(i)}), y^{(i)}) + \lambda r(w)
  • R(h)=EX,Y[l(h(X),Y)]R(h) = E_{X, Y} [l(h(X), Y)]
  • Risk of a prediction function hh

Warning

How can we minimize the risk without knowing the true distribution.

Empirical Risk Minimization (ERM)

min⁡w1N∑i=1Nl(hw(x(i)),y(i))⏟loss⏟empirical risk\min_w \underbrace{\frac{1}{N} \sum^N_{i = 1} \underbrace{l(h_w(x^{(i)}), y^{(i)})}_{loss}}_{\text{empirical risk}}
  • empirical risk (EM) is the average loss over all the data points
  • ERM is a general method to bring down the empirical risk
  • Choose ww by attempting to match given dataset well, as measured by the loss ll

An example of a very poor predictor

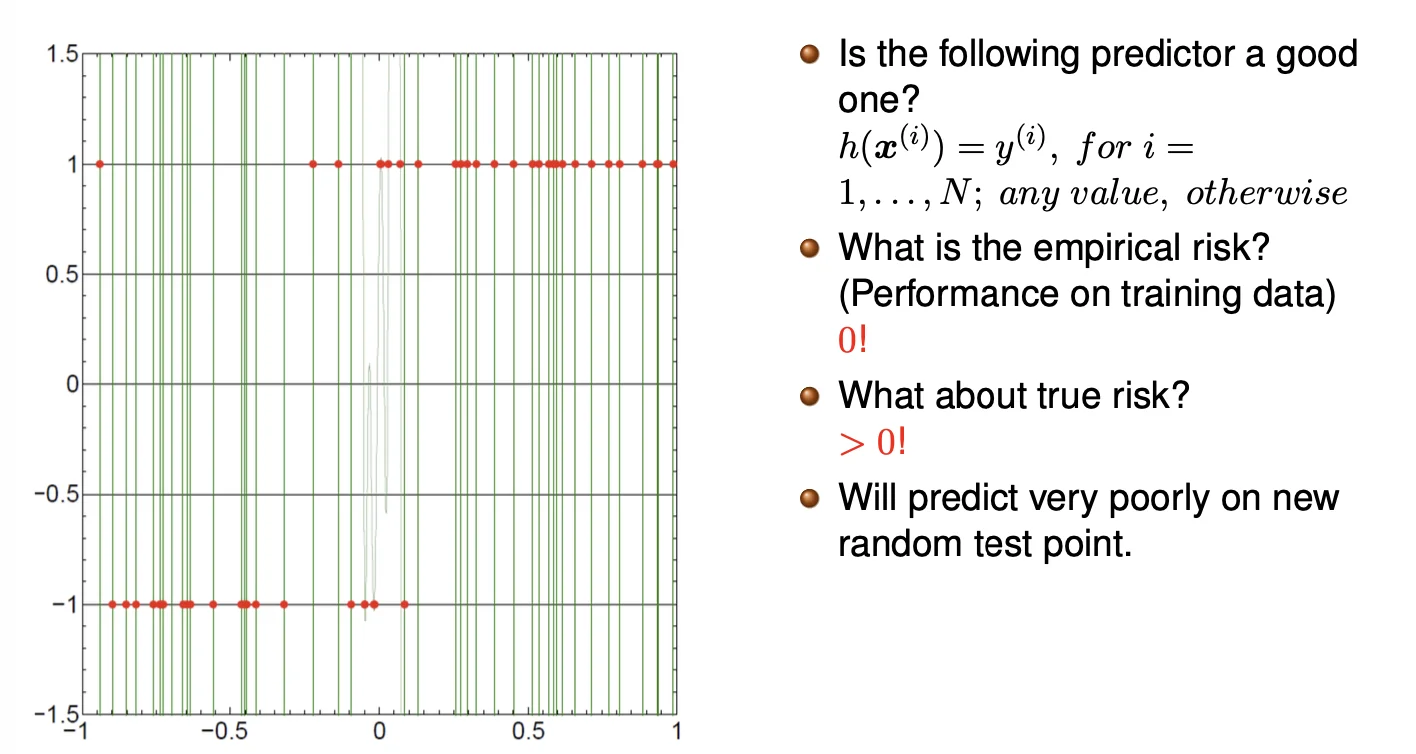
Screenshot 2025-10-16 at 16.34.12

  • Does not generalize at all since h(x(i))=y(i)h(x^{(i)}) = y^{(i)}

Regularized Empirical Risk Minimization

min⁡w1N∑i=1Nl(hw(x(i)),y(i))+λr(w)\min_w \frac{1}{N} \sum^N_{i = 1} l(h_w(x^{(i)}), y^{(i)}) + \lambda r(w)
  • When λ=0\lambda = 0, RERM becomes ERM

Commonly used Binary Classification Loss Function

y∈{−1,1}y \in \{-1, 1\}

∙\bullet Hinge Loss

max⁡[1−y(i)hw(x(i)),0]p\max \left[1 - y^{(i)}h_w(x^{(i)}), 0\right]^p
  • p = 1: standard SVM
  • p = 2: squared hingeless SVM

∙\bullet Log Loss

log⁡(1+e−y(i)hw(x(i)))\log(1 + e^{-y^{(i)}h_w(x^{(i)})})
  • Logistic regression
  • outputs are well-calibrated probabilities

∙\bullet Exponential Loss

e−y(i)hw(x(i))e^{-y^{(i)}h_w(x^{(i)})}
  • AdaBoost
  • Mis-prediction can lead to exponential loss
  • Nice convergence result but fail to handle noisy data well.

∙\bullet Zero-One Loss

I(hw(x(i))≠y(i))I(e){1(e is False)0(e is True)\begin{align*} &\mathbb{I}(h_w(x^{(i)}) \ne y^{(i)}) \\ &\mathbb{I(e)}\begin{cases} 1 \quad (\text{e is }False) \\ 0 \quad (\text{e is }True) \end{cases} \end{align*}
  • Actual classification loss
  • Non-continuous and impractical to optimize

Plots

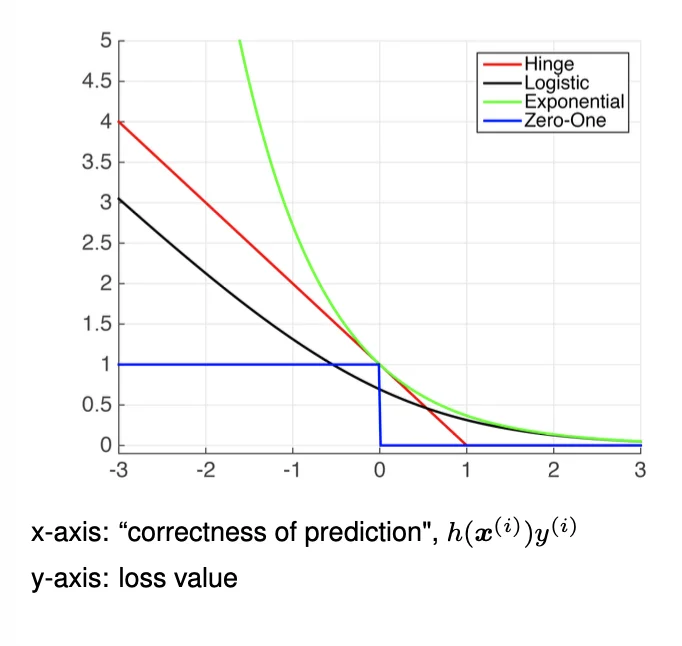
Screenshot 2025-10-16 at 17.00.10

  • Hinge Loss and Exponential Loss are the upper bounds of the zero-one loss

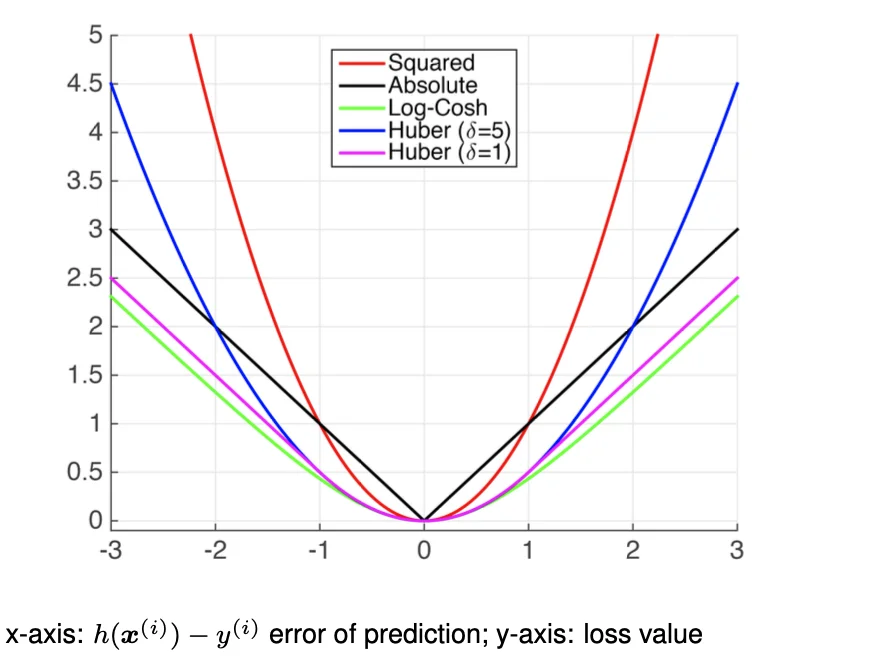
Commonly Used Regression Loss Functions

y∈R1y \in \R^1

∙\bullet Squared Loss

(hw(x(i))−y(i))2\left(h_w(x^{(i)}) - y^{(i)}\right)^2
  • Most popular
  • Also known as Ordinary Least Squares (OLS)
  • Estimates mean label
  • Pros:
  • differentiable everywhere
  • Cons:
  • sensitive to outliers/noise

∙\bullet Absolute Loss

∣hw(x(i))−y(i)∣|h_w(x^{(i)}) - y^{(i)}|
  • Estimates median label
  • Pros:
  • Less sensitive to noises
  • Cons:
  • Not differentiable at 0

∙\bullet Huber Loss

{12(hw(x(i))−y(i))2(∣hw(x(i))−y(i)>δ∣)δ(∣hw(x(i)−y(i))∣−δ2)(otherwise)\begin{cases} \frac{1}{2} (h_w(x^{(i)}) - y^{(i)})^2 \quad\quad(\mid h_w(x^{(i)}) - y^{(i)} > \delta \mid) \\ \delta(\mid h_w(x^{(i)} - y^{(i)})\mid - \frac{\delta}{2}) \quad\quad(otherwise) \\ \end{cases}
  • Also known as Smooth Absolute Loss
  • Set a threshold δ\delta
  • loss>δloss > \delta: Large error, absolute loss
  • loss<δloss < \delta: Small error, squared loss

∙\bullet Log-cosh loss

log⁡(cosh⁡(hw(x(i))−y(i)))\log(\cosh(h_w(x^{(i)}) - y^{(i)}))

where

cosh(x)=ex+e−x2cosh(x) = \frac{e^x + e^{-x}}{2}

Plots

Screenshot 2025-10-16 at 17.24.25

Regularizers

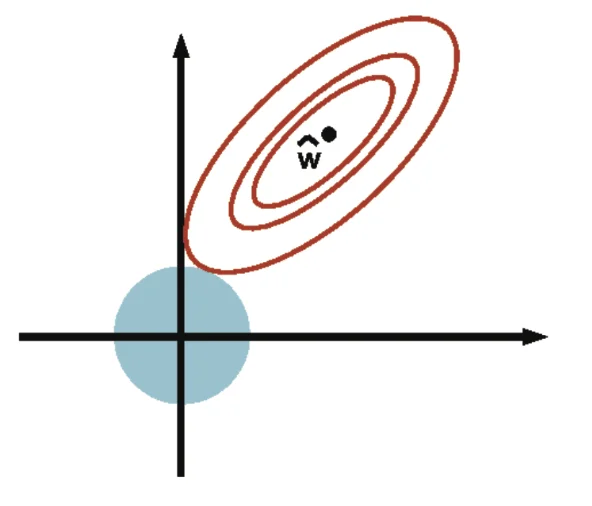
Screenshot 2025-10-16 at 17.28.07

min⁡w1N∑i=1Nl(hw(x(i)),y(i))−λr(w)  ⟺  min⁡w1N∑i=1Nl(hw(x(i)),y(i))s.t.r(w)≤B\begin{align*} &\min_w \frac{1}{N} \sum^N_{i = 1} l(h_w(x^{(i)}), y^{(i)}) - \lambda r(w) \\ &\iff \min_w \frac{1}{N} \sum^N_{i = 1} l(h_w(x^{(i)}), y^{(i)}) \quad s.t. \quad r(w) \le B \end{align*}
  • ∀λ,λ≥0  ⟹  ∃B≥0 s.t. the above formulations hold\forall \lambda, \lambda \ge 0 \implies \exists B\ge 0 \\ \text{ s.t. the above formulations hold}

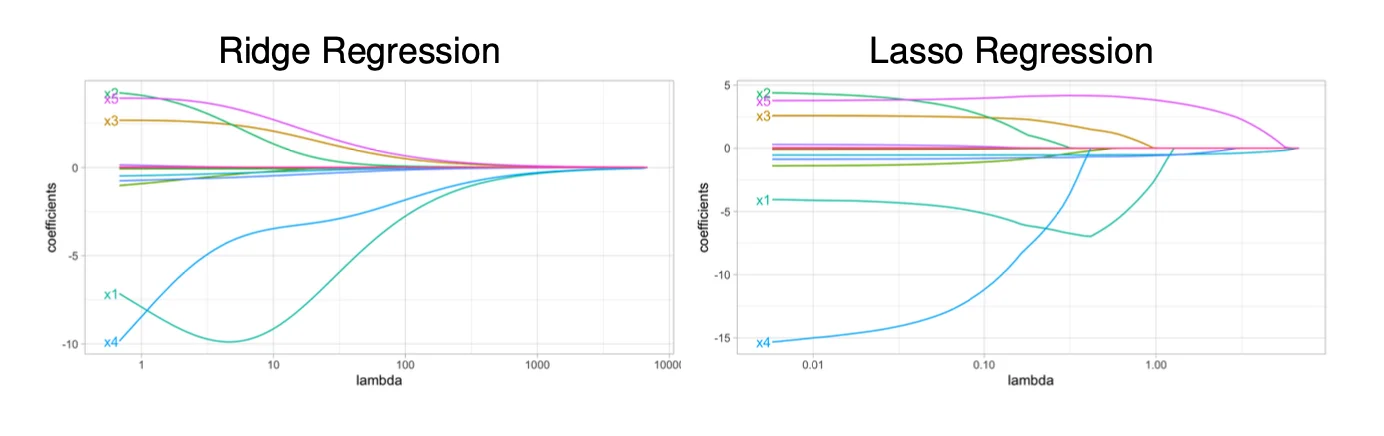
Types of Regularizers

l2−regularizationl_2 - regularization

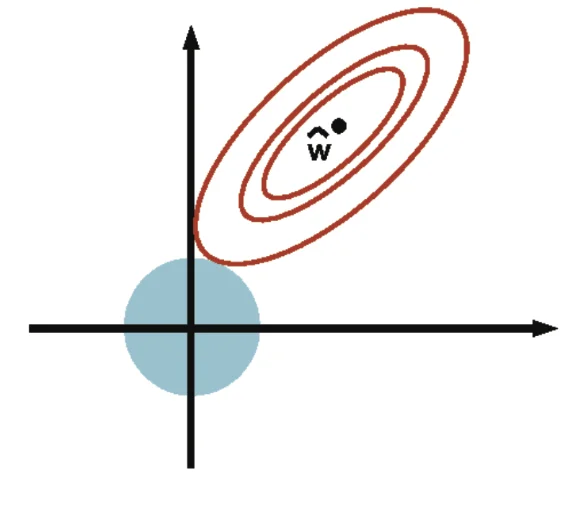
clipboard.png

r(w)=w⊺w=∣∣w∣∣22r(w) = w^\intercal w = ||w||^2_2
  • strictly convex (+)
  • differentiable (+)
  • uses weights on all features (-)

l1−regularizationl_1 - regularization

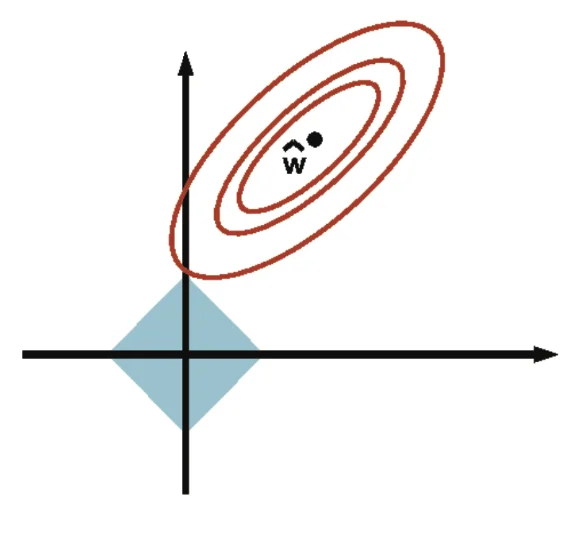
clipboard.png

r(w)=∣∣w∣∣1r(w) = ||w||_1
  • convex (but not strictly)
  • not differentiable at 0 (minimization intends to bring us to)
  • sparse (most of its elements are zeros)

lp−regularizationl_p - regularization

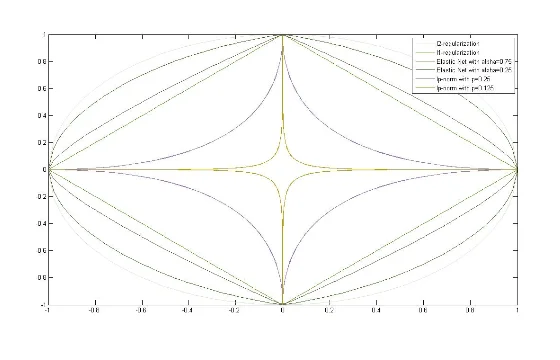
clipboard.png

r(w)=∣∣w∣∣p=(∑i=1Nwip)1pr(w) = ||w||_p = (\sum^N_{i = 1} w^p_i)^\frac{1}{p}
  • non-convex (-)
  • very-sparse solutions (+)
  • initialization-dependent
  • not differentiable (-)

Elastic Net

  • The combination of Lasso (L1) and Ridge (L2) regressions
min⁡w1N∑i=1N(w⊺x(i)−y(i))2+α∣∣w∣∣1+(1−α)∣∣w∣∣22\min_w \frac{1}{N} \sum^N_{i = 1}(w^\intercal x^{(i)} - y^{(i)})^2 + \alpha ||w||_1 + (1 - \alpha)||w||^2_2
  • strictly convex
  • sparsity inducing
  • non-differentiable

clipboard.png