MLE and MAP Proofs
MLE and MAP for Coin Flipping
D \mathcal{D} D α H \alpha_H α H α T \alpha_T α T P ( D ∣ θ ) P(\mathcal{D}|\theta) P ( D ∣ θ )
( α H + α T α H ) θ α H ( 1 − θ ) α T \begin{pmatrix}
\alpha_H + \alpha_T \\
\alpha_H
\end{pmatrix}
\theta^{\alpha_H} (1 - \theta)^{\alpha_T} ( α H + α T α H ) θ α H ( 1 − θ ) α T MLE Proof
θ ^ M L E = arg max θ ( α H + α T α H ) θ α H ( 1 − θ ) α T = arg max θ { ln ( θ α H ( 1 − θ ) α T ) } = arg max θ { α H ln θ + α T ln ( 1 − θ ) } ⇒ 0 = ∂ ∂ θ ( α H ln θ + α T ln ( 1 − θ ) ) ⇒ 0 = α H θ − α T 1 − θ ⇒ θ ^ M L E = α H α H + α T \begin{align*}
\hat{\theta}^{MLE}
&= \argmax_{\theta}
\begin{pmatrix}
\alpha_H + \alpha_T \\
\alpha_H
\end{pmatrix}
\theta^{\alpha_H} (1 - \theta)^{\alpha_T} \\
&= \argmax_{\theta}\{ \ln{(\theta^{\alpha_H}(1 - \theta)^{\alpha_T})} \} \\
&= \argmax_{\theta}\{ \alpha_H\ln{\theta} + \alpha_T\ln{(1 - \theta)} \} \\
&\Rightarrow 0 = \frac{\partial}{\partial \theta} (\alpha_H\ln{\theta} + \alpha_T\ln{(1 - \theta)}) \\
&\Rightarrow 0 = \frac{\alpha_H}{\theta} - \frac{\alpha_T}{1 - \theta} \\
&\Rightarrow \hat{\theta}^{MLE} = \frac{\alpha_H}{\alpha_H + \alpha_T}
\end{align*} θ ^ M L E = θ arg max ( α H + α T α H ) θ α H ( 1 − θ ) α T = θ arg max { ln ( θ α H ( 1 − θ ) α T ) } = θ arg max { α H ln θ + α T ln ( 1 − θ ) } ⇒ 0 = ∂ θ ∂ ( α H ln θ + α T ln ( 1 − θ ) ) ⇒ 0 = θ α H − 1 − θ α T ⇒ θ ^ M L E = α H + α T α H MAP Proof
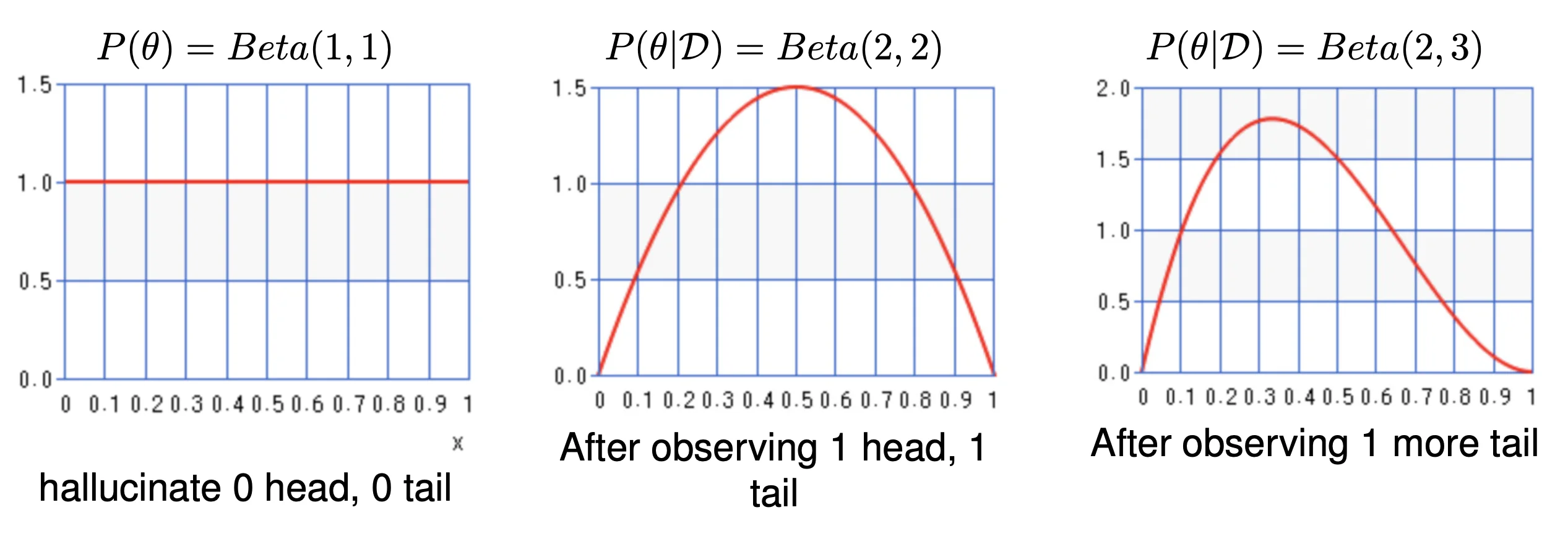
Prior (Beta Distribution)
P ( θ ) = θ β H − 1 ( 1 − θ ) β T − 1 B ( β H , β T ) ∼ B e t a ( β H , β T ) P(\theta) = \frac{\theta^{\beta_{H} - 1} (1 - \theta)^{\beta_T - 1}}{B(\beta_H, \beta_T)} \sim Beta(\beta_H, \beta_T) P ( θ ) = B ( β H , β T ) θ β H − 1 ( 1 − θ ) β T − 1 ∼ B e t a ( β H , β T ) P ( θ ∣ D ) ∝ P ( D ∣ θ ) P ( θ ) ∝ θ α H ( 1 − θ ) α T θ β H − 1 ( 1 − θ ) β T − 1 B ( β H , β T ) ∝ θ α H + β H − 1 ( 1 − θ ) α T + β T − 1 B ( β H , β T ) \begin{align*}
P(\theta \mid \mathcal{D}) &\propto P(\mathcal D \mid \theta)P(\theta) \\
&\propto \theta^{\alpha_H}(1-\theta)^{\alpha_T}\frac{\theta^{\beta_{H} - 1} (1 - \theta)^{\beta_T - 1}}{B(\beta_H, \beta_T)} \\
&\propto \frac{\theta^{\alpha_H + \beta_{H} - 1} (1 - \theta)^{\alpha_T + \beta_T - 1}}{B(\beta_H, \beta_T)}
\end{align*} P ( θ ∣ D ) ∝ P ( D ∣ θ ) P ( θ ) ∝ θ α H ( 1 − θ ) α T B ( β H , β T ) θ β H − 1 ( 1 − θ ) β T − 1 ∝ B ( β H , β T ) θ α H + β H − 1 ( 1 − θ ) α T + β T − 1 θ ^ M A P = arg max θ θ α H + β H − 1 ( 1 − θ ) α T + β T − 1 B ( β H , β T ) = arg max θ θ α H + β H − 1 ( 1 − θ ) α T + β T − 1 ( B ( β H , β T ) does not depend on θ ) = arg max θ ( α H + β H − 1 ) ln θ + ( α T + β T − 1 ) ln ( 1 − θ ) ⇒ 0 = ∂ ∂ θ ( α H + β H − 1 ) ln θ + ( α T + β T − 1 ) ln ( 1 − θ ) ⇒ 0 = ( α H + β H − 1 ) θ + ( α T + β T − 1 ) ( 1 − θ ) ⇒ θ ^ M A P = ( α H + β H − 1 ) ( α T + β T − 1 ) + ( α H + β H − 1 ) \begin{align*}
\hat{\theta}^{MAP}
&= \argmax_{\theta}\frac{\theta^{\alpha_H + \beta_{H} - 1} (1 - \theta)^{\alpha_T + \beta_T - 1}}{B(\beta_H, \beta_T)} \\
&= \argmax_{\theta}\theta^{\alpha_H + \beta_{H} - 1} (1 - \theta)^{\alpha_T + \beta_T - 1} \quad (B(\beta_H, \beta_T) \text{ does not depend on } \theta)\\
&= \argmax_{\theta}(\alpha_H + \beta_{H} - 1)\ln\theta + (\alpha_T + \beta_T - 1)\ln(1 - \theta) \\
&\Rightarrow 0 = \frac{\partial}{\partial\theta}(\alpha_H + \beta_{H} - 1)\ln\theta + (\alpha_T + \beta_T - 1)\ln(1 - \theta) \\
&\Rightarrow 0 = \frac{(\alpha_H + \beta_{H} - 1)}{\theta} + \frac{(\alpha_T + \beta_T - 1)}{(1 - \theta)} \\
&\Rightarrow \hat{\theta}^{MAP} = \frac{(\alpha_H + \beta_{H} - 1)}{(\alpha_T + \beta_T - 1) + (\alpha_H + \beta_{H} - 1)}
\end{align*} θ ^ M A P = θ arg max B ( β H , β T ) θ α H + β H − 1 ( 1 − θ ) α T + β T − 1 = θ arg max θ α H + β H − 1 ( 1 − θ ) α T + β T − 1 ( B ( β H , β T ) does not depend on θ ) = θ arg max ( α H + β H − 1 ) ln θ + ( α T + β T − 1 ) ln ( 1 − θ ) ⇒ 0 = ∂ θ ∂ ( α H + β H − 1 ) ln θ + ( α T + β T − 1 ) ln ( 1 − θ ) ⇒ 0 = θ ( α H + β H − 1 ) + ( 1 − θ ) ( α T + β T − 1 ) ⇒ θ ^ M A P = ( α T + β T − 1 ) + ( α H + β H − 1 ) ( α H + β H − 1 )
β H − 1 : \beta_H - 1: β H − 1 : β T − 1 : \beta_T - 1: β T − 1 :
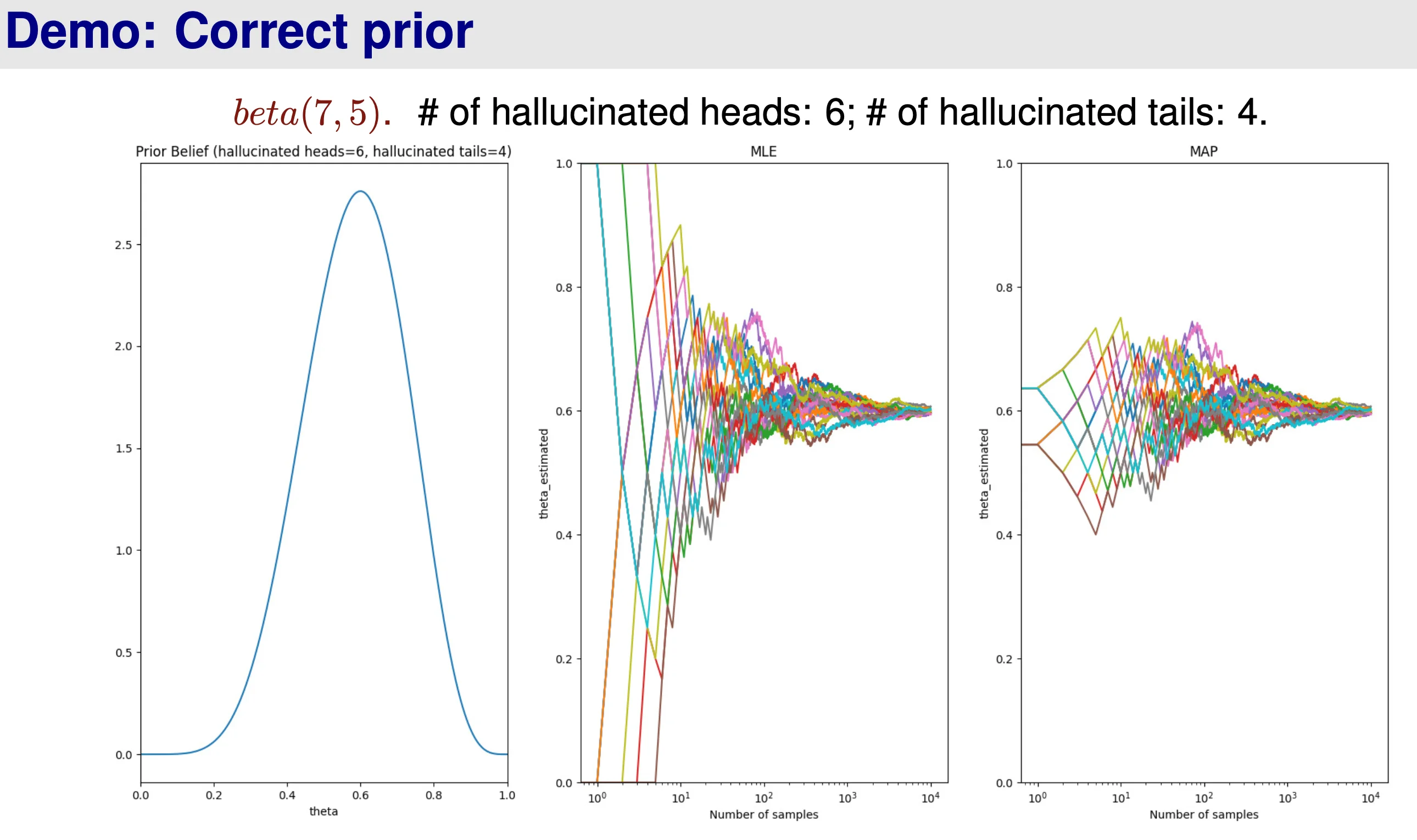
Beta Distribution - Illustration
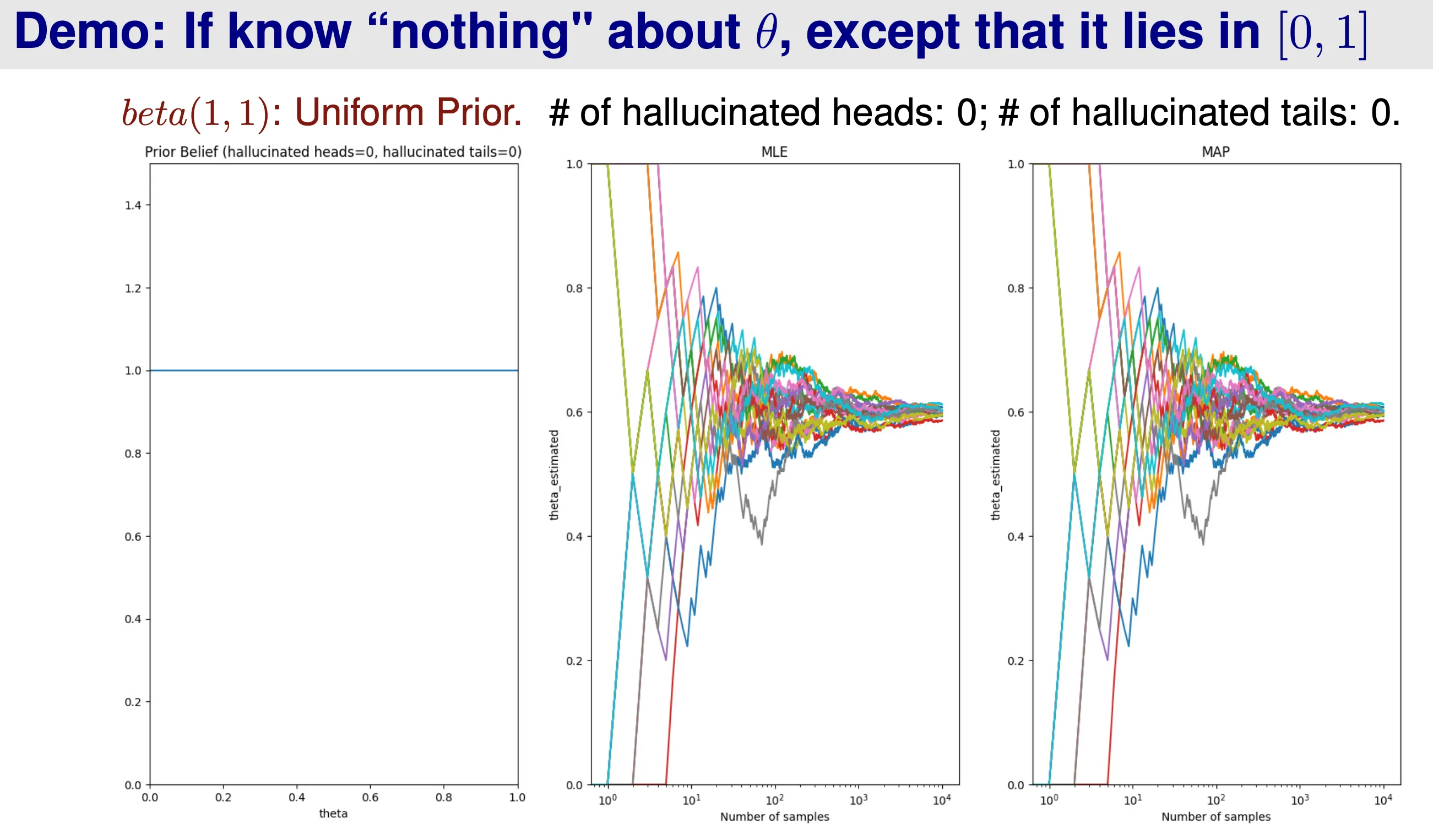
When α H + α T \alpha_H + \alpha_T α H + α T
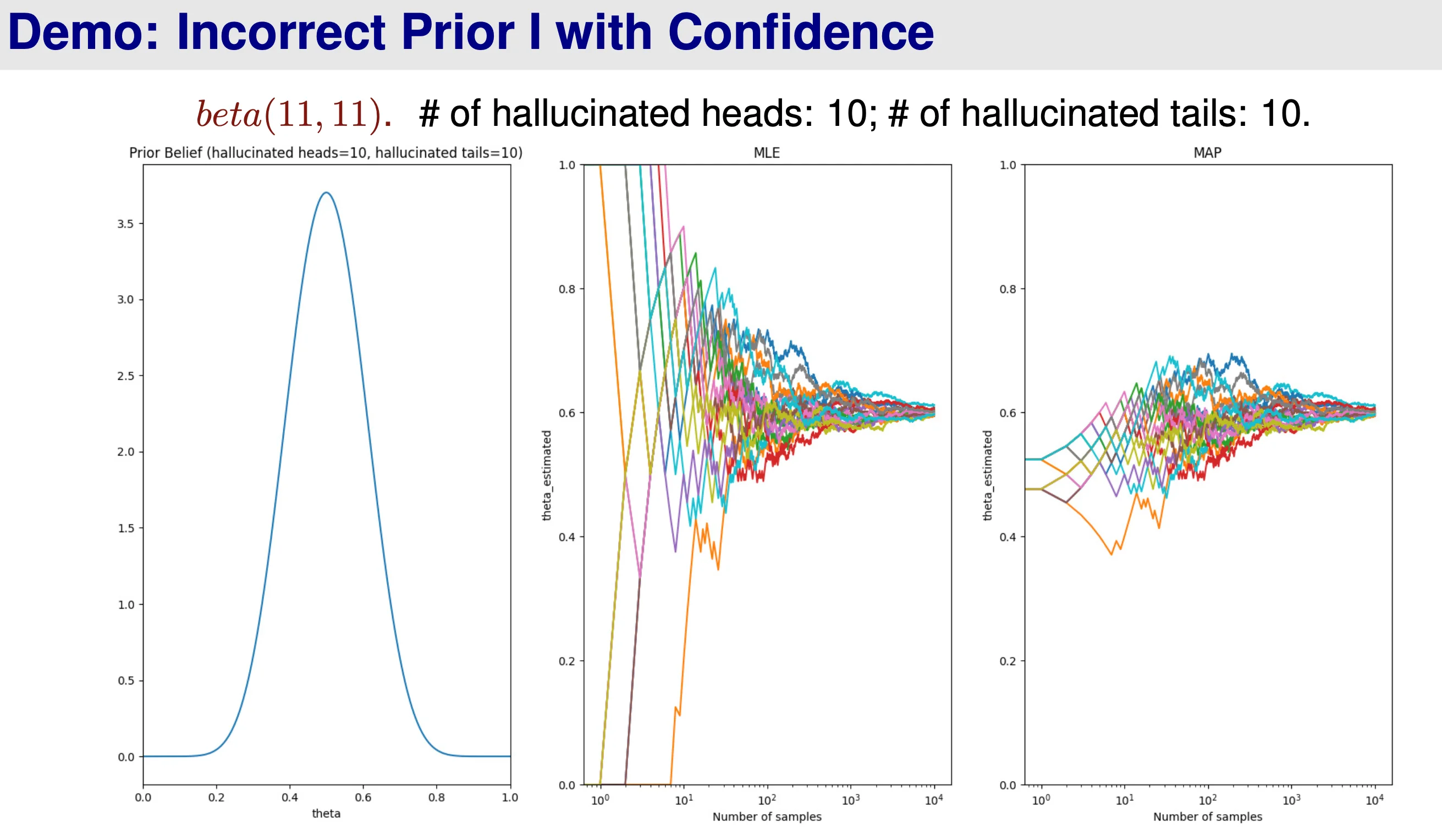
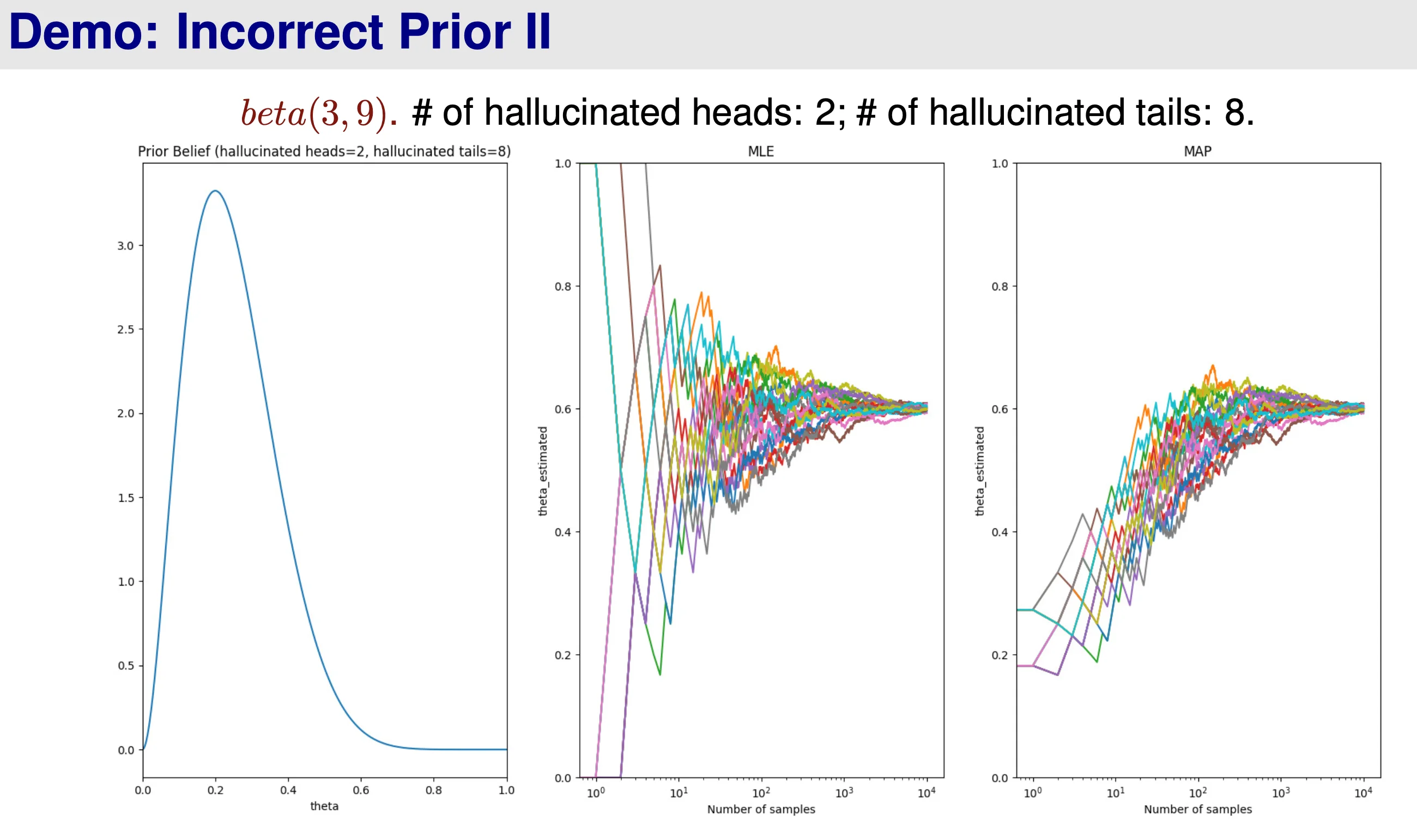
If prior is wrong → \rightarrow →
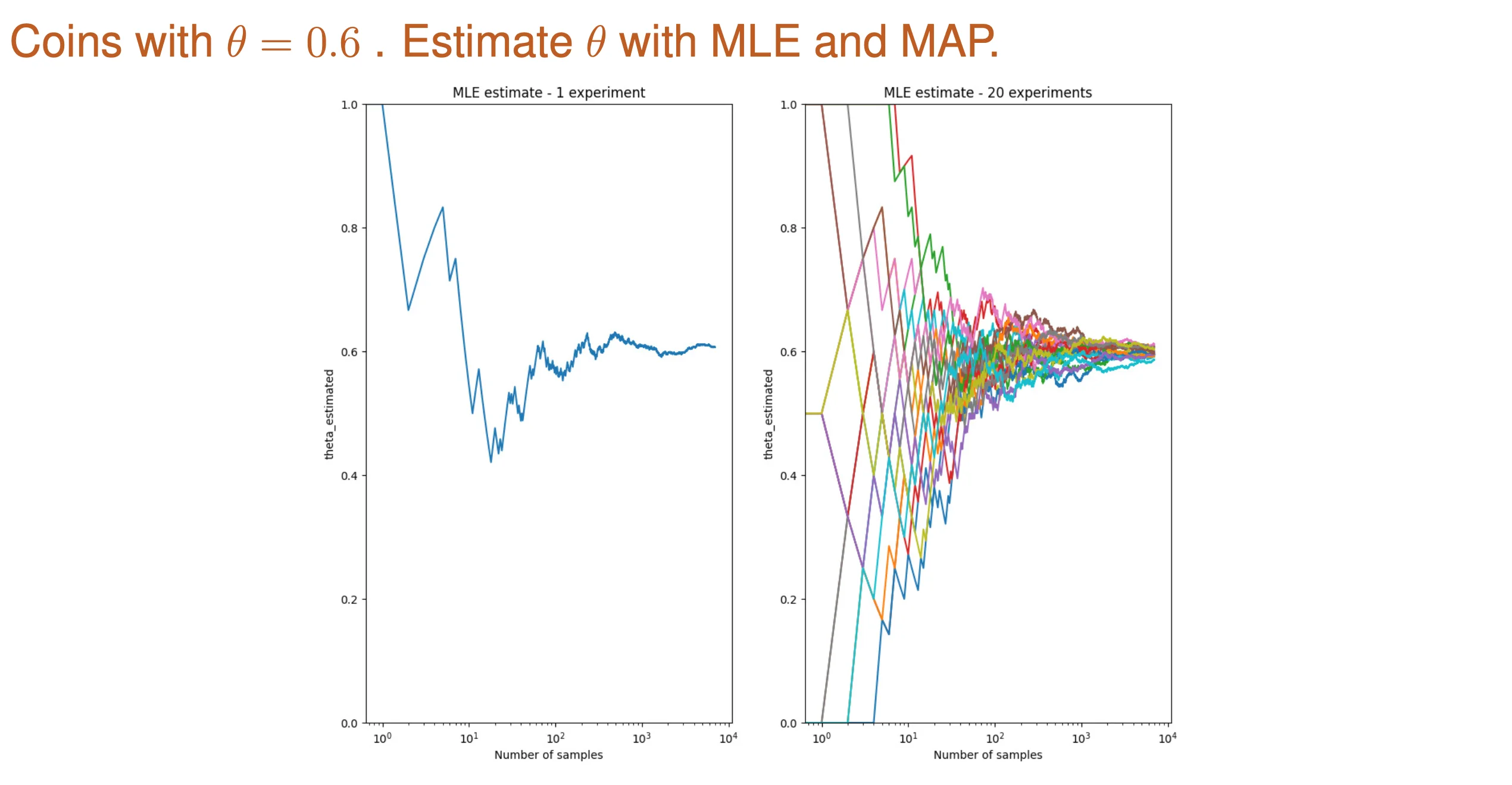
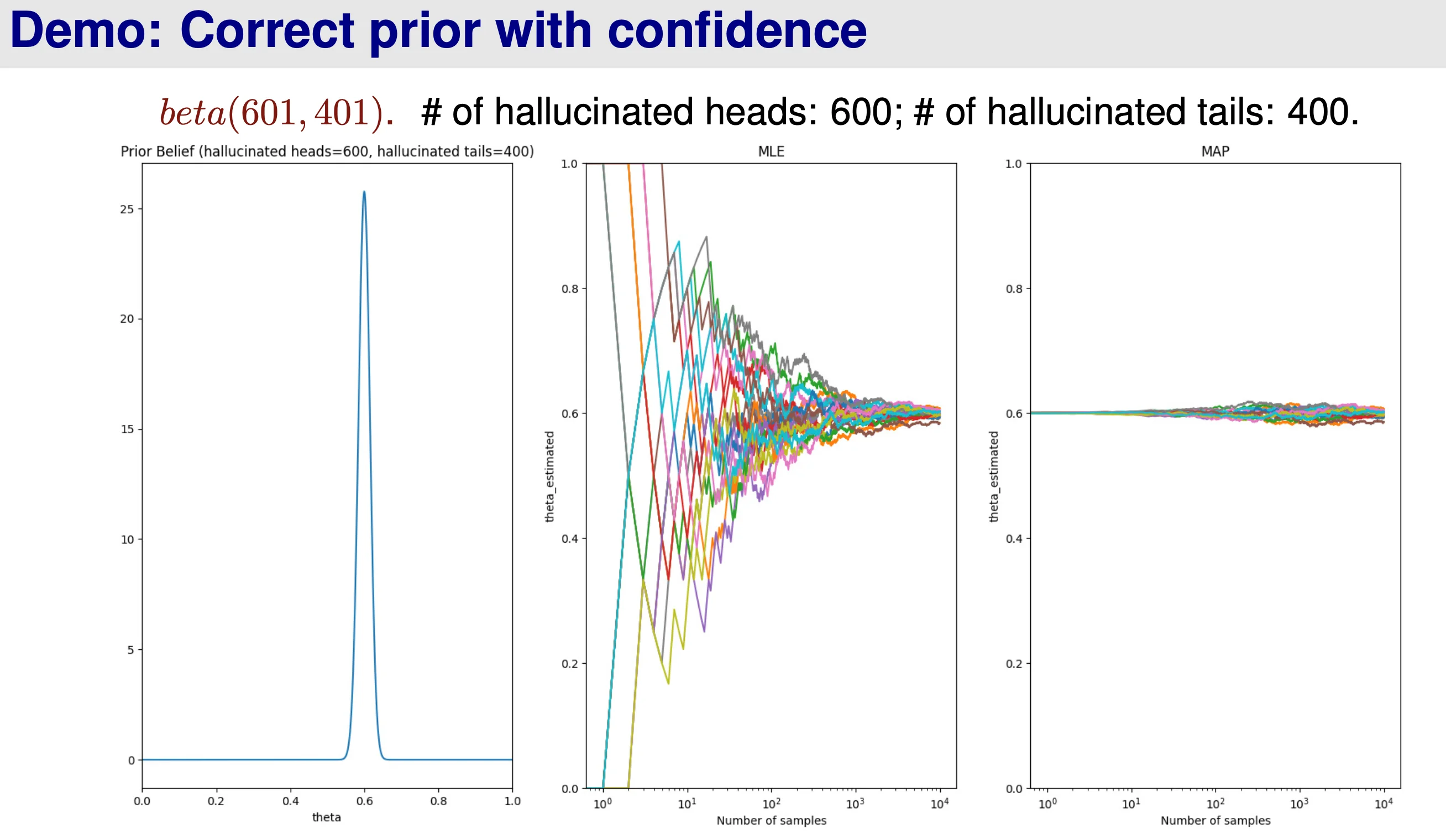
When α H + α T → ∞ \alpha_H + \alpha_T \rightarrow \infty α H + α T → ∞ θ ^ M A P → θ ^ M L E \hat{\theta}^{MAP} \rightarrow \hat{\theta}^{MLE} θ ^ M A P → θ ^ M L E β H \beta_H β H β T \beta_T β T
MLE and MAP of Rolling an M-sided Die
D \mathcal{D} D P ( D ∣ θ ) P(\mathcal{D}|\theta) P ( D ∣ θ ) θ \theta θ { θ 1 , θ 2 , … , θ M } \{\theta_1, \theta_2, \dots, \theta_M\} { θ 1 , θ 2 , … , θ M }
P ( D ∣ θ ) ∝ θ 1 α 1 ⋅ θ 2 α 2 ⋯ θ M α M P(\mathcal{D} | \theta) \propto \theta^{\alpha_1}_1 \cdot \theta^{\alpha_2}_2 \cdots \theta^{\alpha_M}_M P ( D ∣ θ ) ∝ θ 1 α 1 ⋅ θ 2 α 2 ⋯ θ M α M
θ m \theta_m θ m
∙ \bullet ∙ Dirichlet Distribution is used in this case
P ( θ ) = θ 1 β 1 − 1 θ 2 β 2 − 1 ⋯ θ M β M − 1 B ( β 1 , … , B M ) ∼ D i r i c h l e t ( β 1 , … , β M ) P(\theta) = \frac{\theta^{\beta_1 - 1}_1\theta^{\beta_2 - 1}_2 \cdots \theta^{\beta_M - 1}_M}{B(\beta_1, \dots, B_M)} \sim Dirichlet(\beta_1, \dots, \beta_M) P ( θ ) = B ( β 1 , … , B M ) θ 1 β 1 − 1 θ 2 β 2 − 1 ⋯ θ M β M − 1 ∼ D i r i c h l e t ( β 1 , … , β M ) where B ( β 1 , … , B M ) B(\beta_1, \dots, B_M) B ( β 1 , … , B M )
∙ \bullet ∙ P ( θ ∣ D ) ∝ P ( D ∣ θ ) P ( θ ) ∼ D i r i c h l e t ( α 1 + β 1 , … , α M + β M ) P(\theta | \mathcal{D}) \propto P(\mathcal{D} | \theta) P(\theta) \sim Dirichlet(\alpha_1 + \beta_1, \dots, \alpha_M + \beta_M) P ( θ ∣ D ) ∝ P ( D ∣ θ ) P ( θ ) ∼ D i r i c h l e t ( α 1 + β 1 , … , α M + β M ) MLE Proof
Given that L ( θ ) = P ( D ∣ θ ) L(\theta) = P(\mathcal{D} | \theta) L ( θ ) = P ( D ∣ θ ) ∑ m = 1 M θ m = 1 \sum^M_{m = 1} \theta_m = 1 ∑ m = 1 M θ m = 1 Lagrangian and log-likelihood as:
l ( θ ) = ln L ( θ ) = ∑ m = 1 M α m ln θ m − λ ( ∑ m = 1 M θ m − 1 ) l(\theta) = \ln L(\theta) = \sum^M_{m=1} \alpha_m \ln \theta_m - \lambda(\sum^M_{m = 1} \theta_m - 1) l ( θ ) = ln L ( θ ) = m = 1 ∑ M α m ln θ m − λ ( m = 1 ∑ M θ m − 1 )
Then, we partially differentiate the it by θ m \theta_m θ m λ \lambda λ
∂ l ∂ θ m = a m θ m − λ = 0 ⇒ θ ^ m M L E = a m λ ∂ l ∂ λ = − ∑ m = 1 M θ m + 1 = 0 ⇒ ∑ m = 1 M θ ^ m M L E = 1 ⇒ ∑ m = 1 M a m λ = 1 ⇒ ∑ m = 1 M a m = λ ⇒ θ ^ m M L E = a m ∑ v = 1 M a v \begin{align*}
&\begin{align*}
\frac{\partial l}{\partial \theta_m} &= \frac{a_m}{\theta_m} - \lambda = 0 \\
&\Rightarrow \hat{\theta}^{MLE}_{m} = \frac{a_m}{\lambda}
\end{align*} \\
&\begin{align*}
\frac{\partial l}{\partial \lambda} &= -\sum^M_{m = 1} \theta_m + 1 = 0 \\
&\Rightarrow \sum^M_{m = 1} \hat{\theta}_m^{MLE} = 1 \\
&\Rightarrow \sum^M_{m = 1} \frac{a_m}{\lambda} = 1 \\ &\Rightarrow \sum^M_{m = 1} a_m = \lambda
\end{align*}\\
&\Rightarrow \hat{\theta}_m^{MLE} = \frac{a_m}{\sum^M_{v = 1} a_v}
\end{align*} ∂ θ m ∂ l = θ m a m − λ = 0 ⇒ θ ^ m M L E = λ a m ∂ λ ∂ l = − m = 1 ∑ M θ m + 1 = 0 ⇒ m = 1 ∑ M θ ^ m M L E = 1 ⇒ m = 1 ∑ M λ a m = 1 ⇒ m = 1 ∑ M a m = λ ⇒ θ ^ m M L E = ∑ v = 1 M a v a m
Therefore, we can derive that:
θ ^ m M L E = a m ∑ v = 1 M a v \hat{\theta}_m^{MLE} = \frac{a_m}{\sum^M_{v = 1} a_v} θ ^ m M L E = ∑ v = 1 M a v a m MAP Proof
The derivation is similar to the MLE, but we change the likelihood part to posterior
P ( θ ∣ D ) = ∑ m = 1 M ( α m + β m − 1 ) ln θ m − λ ( ∑ m = 1 M θ m − 1 ) P(\theta | \mathcal{D}) = \sum^M_{m =1} (\alpha_m + \beta_m - 1) \ln \theta_m - \lambda(\sum^M_{m = 1} \theta_m - 1) P ( θ ∣ D ) = m = 1 ∑ M ( α m + β m − 1 ) ln θ m − λ ( m = 1 ∑ M θ m − 1 ) ∂ l ∂ θ m = α m + β m − 1 θ m − λ = 0 ⇒ θ ^ m M A P = α m + β m − 1 λ ∂ l ∂ λ ⇒ ∑ m = 1 M α m + β m − 1 λ = 1 ⇒ λ = ∑ m = 1 M α m + β m − 1 ⇒ θ ^ m M A P = α m + β m − 1 ∑ v = 1 M ( α v + β v − 1 ) \begin{align*}
\frac{\partial l}{\partial \theta_m} &= \frac{\alpha_m + \beta_m - 1}{\theta_m} - \lambda = 0 \\
&\Rightarrow \hat{\theta}^{MAP}_m = \frac{\alpha_m + \beta_m -1}{\lambda} \\
\frac{\partial l}{\partial \lambda}&\Rightarrow \sum^M_{m = 1} \frac{\alpha_m + \beta_m -1}{\lambda} = 1 \\
&\Rightarrow \lambda = \sum^M_{m = 1} \alpha_m + \beta_m -1 \\
\end{align*} \\
\Rightarrow \hat\theta^{MAP}_m = \frac{\alpha_m + \beta_m - 1}{\sum^M_{v = 1} (\alpha_v + \beta_v -1)} ∂ θ m ∂ l ∂ λ ∂ l = θ m α m + β m − 1 − λ = 0 ⇒ θ ^ m M A P = λ α m + β m − 1 ⇒ m = 1 ∑ M λ α m + β m − 1 = 1 ⇒ λ = m = 1 ∑ M α m + β m − 1 ⇒ θ ^ m M A P = ∑ v = 1 M ( α v + β v − 1 ) α m + β m − 1 θ ^ m M A P = α m + β m − 1 ∑ v = 1 M ( α v + β v − 1 ) \hat\theta^{MAP}_m = \frac{\alpha_m + \beta_m - 1}{\sum^M_{v = 1} (\alpha_v + \beta_v -1)} θ ^ m M A P = ∑ v = 1 M ( α v + β v − 1 ) α m + β m − 1